An object of mass m slides down a hill of arbitrary shape and after travelling a certain horizontal path stops because of friction. The total vertical height descended is h. The friction coefficient is different for different segments for the entire path but is independent of the velocity and direction of motion. The work that a tangerial force must perform to return the object to its initial position along the same path is
(a) mgh
(b) −mgh
(c) −2mgh
(d) 2mgh
The correct Answer is:D
To solve the problem, we need to determine the total work done by a tangential force to return the object to its initial position along the same path after it has slid down a hill and stopped due to friction.
1. Understanding the Problem:
- An object of mass m slides down a hill and descends a vertical height h.
- The object stops due to friction, which varies along the path.
- We need to find the work done by a tangential force to bring the object back to its starting point.
2. Work Against Gravity:
- When the object is raised back to its initial position, it must overcome the gravitational potential energy lost while sliding down.
- The work done against gravity (to raise the object back up) is given by:
Wgravity=mgh
3. Work Done Against Friction:
- As the object slides down, friction does negative work on the object, which can be equated to the loss of potential energy.
- The total work done by friction as the object slides down is equal to the potential energy lost:
Wfriction=−mgh
- Since the work done by friction is negative, the work done against friction when bringing the object back up will be the same magnitude but positive:
Wagainst friction=mgh
4. Total Work Done by Tangential Force:
- The total work done by the tangential force to return the object to its initial position is the sum of the work done against gravity and the work done against friction:
Wtotal=Wgravity+Wagainst friction=mgh+mgh=2mgh
5. Final Answer:
- Therefore, the total work that a tangential force must perform to return the object to its initial position along the same path is:
2mgh
- An object of mass m slides down a hill and descends a vertical height h.
- The object stops due to friction, which varies along the path.
- We need to find the work done by a tangential force to bring the object back to its starting point.
- When the object is raised back to its initial position, it must overcome the gravitational potential energy lost while sliding down.
- The work done against gravity (to raise the object back up) is given by:
Wgravity=mgh
- As the object slides down, friction does negative work on the object, which can be equated to the loss of potential energy.
- The total work done by friction as the object slides down is equal to the potential energy lost:
Wfriction=−mgh
- Since the work done by friction is negative, the work done against friction when bringing the object back up will be the same magnitude but positive:
Wagainst friction=mgh
- The total work done by the tangential force to return the object to its initial position is the sum of the work done against gravity and the work done against friction:
Wtotal=Wgravity+Wagainst friction=mgh+mgh=2mgh
- Therefore, the total work that a tangential force must perform to return the object to its initial position along the same path is:
2mgh
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
What is the ratio of displacement to the path length traversed by an object, if the object comes back to its initial position?
View SolutionA mass m slides down a fixed plane inclined at an angle a to the horizontal plane after covering the entire length of the inclined plane. The height of the inclined plane is h and the coefficient of friction over both surfaces is μ.
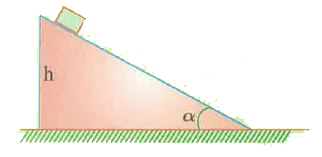
View Solution
Knowledge Check
An object of mass m slides down a hill of height h and of arbitrary shape and stops at the bottom because of friction. The coefficient of friction may be different for different segments of the path. Work required to return the object to its position along the same path by a tangential force is
AmghB2mghC=−mghDit can not be calculatedFor a particle moving in vertical circle, the total energy at different positions along the path
Ais conservedBincreasesCdecreasesDmay increases or decreasesA car travels east with a certain constant velocity. The direction of the friction force on the car is
Adue eastBdue westCupDzero
Represent the motion of an object in unifrom motion along a straight line when both initial distance and velocity of the object is positive .
View SolutionA block of mass m is given velocity v0 on a rough horizontal surface. After traveling a distance d. Its speed becomes (v0)/(2). Find the work done against friction. The work donw by friction and the coefficient of friction.
View SolutionA brick of mass 2kg begins to slide down on a plane inclined at an angle of 45∘ with the horizontal. The force of friction will be
View SolutionA brick of mass 2kg just begins to slide down on inclined plane at an angle of 45∘ with the horizontal. The force of friction will be
View SolutionAn object of mass (m) is located on the horizontal plane at the origin O. The body acquires horizontal velocity V. The mean power developed by the frictional force during the whole time of motion is ( μ= frictional coefficient )
View Solution
