An unruly demonstrator lifts a stone of mass 200 g from the ground and throuws it at his opponent. At the time of projection, the stone is 150 cm above the grond and has a speed of 3.00 m/s. Calculate the work doe by the demonstrator during the process. If it takes one second for the demonstrator tolift teh stone and throw, what horsepower does he use?
The correct Answer is:A, C, D
To solve the problem, we need to calculate the work done by the demonstrator while lifting and throwing the stone, and then convert that work into horsepower.
Step 1: Identify the given data
- Mass of the stone (m) = 200 g = 0.2 kg (since 1 g = 0.001 kg)
- Height above the ground (h) = 150 cm = 1.5 m (since 1 cm = 0.01 m)
- Speed at the time of projection (v) = 3.00 m/s
- Acceleration due to gravity (g) = 10 m/s² (standard approximation)
Step 2: Calculate the change in potential energy (PE)
The potential energy at the height is given by the formula:
PE=m⋅g⋅h
Substituting the values:
PE=0.2kg⋅10m/s2⋅1.5m=3J
Step 3: Calculate the change in kinetic energy (KE)
The kinetic energy at the time of projection is given by the formula:
KE=12mv2
Substituting the values:
KE=12⋅0.2kg⋅(3.00m/s)2=12⋅0.2⋅9=0.9J
Step 4: Calculate the total work done (W)
The total work done by the demonstrator is the sum of the change in potential energy and the change in kinetic energy:
W=PE+KE=3J+0.9J=3.9J
Step 5: Calculate the power in watts
Power (P) is defined as work done per unit time. Since the work is done in 1 second:
P=Wt=3.9J1s=3.9W
Step 6: Convert power to horsepower
1 horsepower (hp) is equivalent to 746 watts. To convert watts to horsepower:
Horsepower=P746=3.9W746≈0.00522hp
Final Result
The work done by the demonstrator is 3.9 J, and the power used is approximately 0.00522 hp.
---
- Mass of the stone (m) = 200 g = 0.2 kg (since 1 g = 0.001 kg)
- Height above the ground (h) = 150 cm = 1.5 m (since 1 cm = 0.01 m)
- Speed at the time of projection (v) = 3.00 m/s
- Acceleration due to gravity (g) = 10 m/s² (standard approximation)
The potential energy at the height is given by the formula:
PE=m⋅g⋅h
Substituting the values:
PE=0.2kg⋅10m/s2⋅1.5m=3J
The kinetic energy at the time of projection is given by the formula:
KE=12mv2
Substituting the values:
KE=12⋅0.2kg⋅(3.00m/s)2=12⋅0.2⋅9=0.9J
The total work done by the demonstrator is the sum of the change in potential energy and the change in kinetic energy:
W=PE+KE=3J+0.9J=3.9J
Power (P) is defined as work done per unit time. Since the work is done in 1 second:
P=Wt=3.9J1s=3.9W
1 horsepower (hp) is equivalent to 746 watts. To convert watts to horsepower:
Horsepower=P746=3.9W746≈0.00522hp
The work done by the demonstrator is 3.9 J, and the power used is approximately 0.00522 hp.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer16videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -28videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
Similar Questions
A popular game in Indian villages is goli which is played with small glass balls called golis. The goli of one player is situatted at a distance of 2.0 m from the goli of the second player. This second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middlefilngers and making the throw. If he projected is 19.6 cm from the ground and the goli is to be projected horizontally, with what speed shold it be projected so that it directly hits the stationary goli without falling on the ground earlier?
View SolutionA boy on a lift 490 m high drops a stone. One second later, he throws a second stone after the first. They hit the ground at the same time. With what speed did he thrown the second stone.
View SolutionDuring summer season,a child was walking through a garden where he saw a mango on the tree at a height of 20m ,he decides to throw a stone and break it from the tree so he picks up a stone and throws it vertically upwards the mango .The stone hits the mango after exactly 2s seconds ,then the speed withnwhich the stone was thrown upwards (take g=10m/x2)
View SolutionDuring summer season,a child was walking through a garden where he saw a mango on the tree at a height of 20m ,he decides to throw a stone and break it from the tree so he picks up a stone and throws it vertically upwards the mango .The stone hits the mango after exactly 2s seconds ,then the speed withnwhich the stone was thrown upwards (take g=10m/x2)
View SolutionDuring summer season,a child was walking through a garden where he saw a mango on the tree at a height of 20m ,he decides to throw a stone and break it from the tree so he picks up a stone and throws it vertically upwards the mango .The stone hits the mango after exactly 2s seconds ,then the speed withnwhich the stone was thrown upwards (take g=10m/x2)
View SolutionAn object A is kept fixed at the point x=3m and y=1.25m on a plank p raised above the ground . At time t=0 the plank starts moving along the +x direction with an acceleration 1.5m/s2. At the same instant a stone is projected from the origin with a velocity →u as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle 45(∘) to the horizontal . All the motions are in the X−Yplane . Find →u and the time after which the stone hits the object . Take g=10m/s
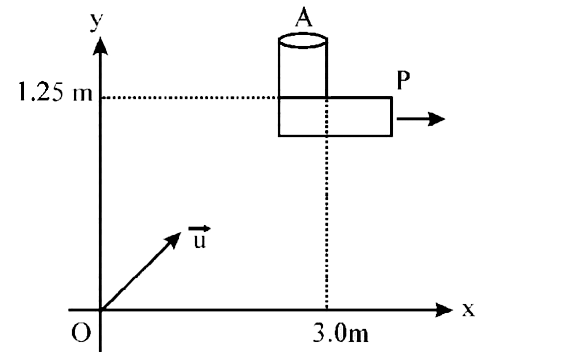 View Solution
View SolutionAn object A is kept fixed at the point x=3m and y=1.25m on a plank p raised above the ground . At time t=0 the plank starts moving along the +x direction with an acceleration 1.5m/s2. At the same instant a stone is projected from the origin with a velocity →u as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle 45(∘) to the horizontal . All the motions are in the X−Yplane . Find →u and the time after which the stone hits the object . Take g=10m/s
 View Solution
View Solutionsmall block of mass 200 g is kept at the top of a frictionless incline which is 10 m long and 3.2 m high. How much work was required a. to lift the block from the ground nd put it at the top b. to side the block up the incline? What will be the speed of the block when it reaches the ground if, c. it falls off the incline and drops vertically on the ground d. it slides down the incline? Take g=10ms2.
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
A small sphere of mass 2.00 g is released from rest in a large vessel filled with oil. The sphere approaches a terminal speed of 10.00 cm/s. Time required to achieve speed 6.32 cm/s from start of the motion is (Take g=10.00m/s2) :View Solution

