Angular impulse J is applied on a system which can rotate about an axis for which its moment of inertia is I. System is initially at rest.
Angular momentum of the system becomes J
Angular velocity acquired by the system is J/I
Kinetic energy acquired by the system is J22I
Angular momentum of the system becomes J/I
The correct Answer is:A, B, C
To solve the problem step by step, we need to analyze the given information and apply the relevant physics concepts.
Step 1: Understand Angular Impulse
Angular impulse J is defined as the product of torque τ and the time duration dt over which the torque is applied. Mathematically, it can be expressed as:
J=τ⋅dt
Step 2: Relate Torque to Angular Acceleration
Torque τ can also be expressed in terms of moment of inertia I and angular acceleration α:
τ=I⋅α
Step 3: Relate Angular Acceleration to Angular Velocity
Since the system starts from rest, the initial angular velocity ω0=0. After applying the angular impulse, the final angular velocity is ω. The change in angular velocity dω is:
dω=ω−ω0=ω
Step 4: Substitute into Angular Impulse Equation
Substituting the expression for torque into the angular impulse equation gives:
J=I⋅dω
Since dω=ω, we can rewrite it as:
J=I⋅ω
Step 5: Solve for Angular Velocity
From the equation J=I⋅ω, we can solve for ω:
ω=JI
Step 6: Calculate Angular Momentum
The angular momentum L of the system is given by:
L=I⋅ω
Substituting ω from the previous step:
L=I⋅(JI)=J
Step 7: Calculate Kinetic Energy
The kinetic energy K of a rotating system is given by:
K=12Iω2
Substituting ω from Step 5:
K=12I(JI)2=12I⋅J2I2=J22I
Summary of Results
1. The angular momentum of the system becomes J.
2. The angular velocity acquired by the system is JI.
3. The kinetic energy acquired by the system is J22I.
Conclusion
Based on the analysis, the correct answers to the options provided in the question are:
- Angular momentum becomes J
- Angular velocity acquired is JI
- Kinetic energy acquired is J22I
Angular impulse J is defined as the product of torque τ and the time duration dt over which the torque is applied. Mathematically, it can be expressed as:
J=τ⋅dt
Torque τ can also be expressed in terms of moment of inertia I and angular acceleration α:
τ=I⋅α
Since the system starts from rest, the initial angular velocity ω0=0. After applying the angular impulse, the final angular velocity is ω. The change in angular velocity dω is:
dω=ω−ω0=ω
Substituting the expression for torque into the angular impulse equation gives:
J=I⋅dω
Since dω=ω, we can rewrite it as:
J=I⋅ω
From the equation J=I⋅ω, we can solve for ω:
ω=JI
The angular momentum L of the system is given by:
L=I⋅ω
Substituting ω from the previous step:
L=I⋅(JI)=J
The kinetic energy K of a rotating system is given by:
K=12Iω2
Substituting ω from Step 5:
K=12I(JI)2=12I⋅J2I2=J22I
1. The angular momentum of the system becomes J.
2. The angular velocity acquired by the system is JI.
3. The kinetic energy acquired by the system is J22I.
Based on the analysis, the correct answers to the options provided in the question are:
- Angular momentum becomes J
- Angular velocity acquired is JI
- Kinetic energy acquired is J22I
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )10videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )3videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )48videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
- BOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST15videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View SolutionTwo masses M and m are connect by a light string gong over a pulley of radis r. The pulley is free to rotate about its axis which is kept horizontal. The moment of inertia of the pulley about the axis is I. The system is releaed from rest. Find the angular momentum fo teh system when teh mass Mhas descended through a height h. The string does not slip over the pulley.
View Solution
Knowledge Check
- Question 1 - Select One
Find moment of inertia of system about diagonal of square :-
 A2ml2Bml2Cml22Dml2√2
A2ml2Bml2Cml22Dml2√2 - Question 2 - Select One
Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
A52IB3IC32ID2I - Question 3 - Select One
The moment of an inertia about an axis of a body which is rotating with angular velocity 1rad s−1 is numerically equal to
Aone - fourth of its rotational kinetic energyBhalf of the rotational kinetic energyCrotational kinetic energyDtwice the rotational kinetic energy
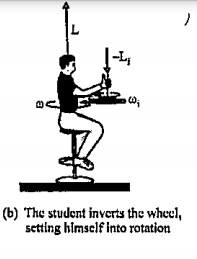
Figure shows a student, sitting on a stool that can rotate freely about a vertical axis. The student, initially at rest, is holding a bicycle wheel whose rim is loaded with lead and whose moment of inertia is I about its central axis. The wheel is rotating at an angular speed ωi from an overead perspective, the rotation is counter clockwise. The axis of the wheel point vertical, and the angular momentum →Li of the wheel points vertically upward. The student now inverts the wheel, as a result, the student and stool rotate about the stool axis. With what angular speed and direction does the student then rotate? (The moment of inertia of the student+stool+wheel system about the stool axis is I0)

 View Solution
View SolutionA ballet dancer is rotating about his own vertical axis at an angular velocity 100r± on smooth horizontal floor. The ballet dancer folds himself close to his axis of rotation by which is moment of inertia decreases to half of initial moment of inertia then his final angular velocity is
View SolutionA stationary horizontal disc is free to rotate about its axis. When a torque is applied on it, its kinetic energy as a function of θ, where θ is the angle by which it has rotated, is given as kθ2 If its moment of inertia is I then the angular acceleration of the disc is
View SolutionA uniform circular disc of radius R is rotating about its own axis with moment of inertia I at an angular velocity ω if a denser particle of mass m is gently attached to the rim of disc than its angular velocity is
View SolutionA disc of radius 10 cm can rotate about an axis passing through its centre and perpendicular to its plane. A force of 10 N is applied along the tangent in the plane of the disc. If the moment of inertia of the disc about its centre is 5kgm2, then the increase in the angular velocity of the disc in 10 s will be
View Solution

