As a 2.5 kg body moves in the positive direction along an x axis, a single force acts on it. The force is given by Fx=−6xN, with x in meters. The velocity at x=3.5m is 8.5 m/s. (a) Find the velocity of the body at x=4.5 m. (b) Find the positive value of x at which the body has a velocity of 5.5 m/s.
The correct Answer is:(a) 7.3 m/s; (b) 5.5 m
To solve the problem, we will follow these steps:
Given Data:
- Mass of the body, m=2.5kg
- Force acting on the body, Fx=−6xN
- Velocity at x=3.5m, v=8.5m/s
Part (a): Find the velocity of the body at x=4.5m
1. Use Newton's Second Law:
F=ma⟹−6x=mdvdt
Since a=dvdt and we can express dvdt in terms of dvdx:
−6x=mvdvdx
2. Rearranging the equation:
vdv=−62.5xdx
vdv=−2.4xdx
3. Integrate both sides:
∫vdv=∫−2.4xdx
v22=−1.2x2+C
4. Find the constant C using the initial condition v=8.5m/s at x=3.5m:
(8.5)22=−1.2(3.5)2+C
36.125=−1.2⋅12.25+C
36.125=−14.7+C⟹C=50.825
5. Substituting C back into the equation:
v22=−1.2x2+50.825
v2=−2.4x2+101.65
6. Find v at x=4.5m:
v2=−2.4(4.5)2+101.65
v2=−2.4⋅20.25+101.65
v2=−48.6+101.65=53.05
v=√53.05≈7.28m/s
Part (b): Find the positive value of x at which the body has a velocity of 5.5m/s
1. Set v=5.5m/s in the equation:
(5.5)2=−2.4x2+101.65
30.25=−2.4x2+101.65
−2.4x2=30.25−101.65
−2.4x2=−71.4⟹x2=71.42.4
x2=29.75⟹x=√29.75≈5.45m
Final Answers:
- (a) The velocity of the body at x=4.5m is approximately 7.28m/s.
- (b) The positive value of x at which the body has a velocity of 5.5m/s is approximately 5.45m.
- Mass of the body, m=2.5kg
- Force acting on the body, Fx=−6xN
- Velocity at x=3.5m, v=8.5m/s
F=ma⟹−6x=mdvdt
Since a=dvdt and we can express dvdt in terms of dvdx:
−6x=mvdvdx
vdv=−62.5xdx
vdv=−2.4xdx
∫vdv=∫−2.4xdx
v22=−1.2x2+C
(8.5)22=−1.2(3.5)2+C
36.125=−1.2⋅12.25+C
36.125=−14.7+C⟹C=50.825
v22=−1.2x2+50.825
v2=−2.4x2+101.65
v2=−2.4(4.5)2+101.65
v2=−2.4⋅20.25+101.65
v2=−48.6+101.65=53.05
v=√53.05≈7.28m/s
(5.5)2=−2.4x2+101.65
30.25=−2.4x2+101.65
−2.4x2=30.25−101.65
−2.4x2=−71.4⟹x2=71.42.4
x2=29.75⟹x=√29.75≈5.45m
- (a) The velocity of the body at x=4.5m is approximately 7.28m/s.
- (b) The positive value of x at which the body has a velocity of 5.5m/s is approximately 5.45m.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
59 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
The acceleration of a particle is given by the relation as a=−kv5/2 , where is a constant. The particle starts at x=0 with a velocity of 16 m/s, and when x = 6, the velocity is observed to be 4 m/s. Find the velocity of particle when x=5m and the time at which the velocity ofthe particle is 9 m/s.
View Solution(b) Find the value of m, if x+2 is a factor of x3−4x2+3x−5m
View Solution
Knowledge Check
A body of mass 10 kg is upon by a force given by equation F=(3t2−30) newtons. The initial velocity of the body is 10 m/s. The velocity of the body after 5 sec. is
A4.5 m/sB6 m/sC7.5 m/sD5 m/sA body moves with velocity v = lnx m/s where x is its position. The net force acting on body is zero at .
A0 mBx=e2mCx=emDx=1mA block of mass 2 kg is having velocity 4√5ms−1 in the positive x - direction at the origin. The only force acting on it is F=(3x2−12x)N. Its velocity when it is at x=2 m is
A8ms−1B4ms−1C10√24ms−1D20ms−1
A particle is moving along x-axis. The position of the particle at any instant is given by x=a+bt2 where ,a= 6 m and b= 3.5 ms−2 't' is measured in second .Find
(i) the velocity of the particle at 1s and
(ii) the average velocity between 3s and 6s
View SolutionAn object is moving along +ve x-axis with a uniform acceleration of 4ms−2 . At time t=0 , x=5m and v=3ms−1 .
(a) What will be the velocity and position of the object at time t=2s?
What will be the velocity and position of the object when it has a velocity of 5ms−1?
View SolutionA 2.00 kg particle moves along an x axis in onedimensional motion while a conservative force along that axis acts on it. The potential energy U(x) associated with the force is plotted in Fig. 8-36a. That is, if the particle were placed at any position between x=0 and x=7.00m, it would have the plotted value of U. At x=6.5m, the particle has velocity →v0=(−4.00m/s)ˆi.
(c) Evaluate the force acting on the particle when it is in the region 1.9 m<x<4.0 m.
View SolutionA body of 5kg is moving with a velocity of 20m/s. If a force of 100N is applied on it for 10 s in the same direction as its velocity, what will now be the velocity of the body?
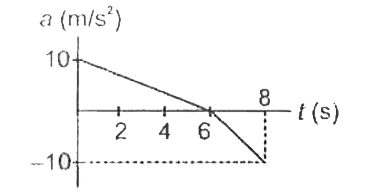
View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
View Solution
