As , can you say that the capacitor is proportion to the charge ?
To determine whether the capacitance C is proportional to the charge Q, we can analyze the relationship given by the formula C=QV.
1. Understanding the Formula:
The formula for capacitance is given by:
C=QV
where C is the capacitance, Q is the charge stored in the capacitor, and V is the voltage across the capacitor.
2. Rearranging the Formula:
From the formula, we can express the charge Q in terms of capacitance C and voltage V:
Q=C⋅V
3. Analyzing Proportionality:
To determine if C is proportional to Q, we need to consider how C behaves when Q changes. The capacitance C is defined as a constant for a given capacitor, depending on its physical characteristics (like area, distance between plates, and dielectric material).
4. Considering Voltage:
If we assume that the voltage V across the capacitor changes, then Q will change proportionally with V if C remains constant. This means:
Q \propto V \quad \text{(if C is constant)}
However, C itself does not change with Q; it is a constant for a specific capacitor configuration.
5. Conclusion:
Since C is a constant and does not vary with the charge Q, we conclude that:
C is not proportional to Q.
Final Statement:
Thus, we can say that the capacitance C is not proportional to the charge Q.
---
The formula for capacitance is given by:
C=QV
where C is the capacitance, Q is the charge stored in the capacitor, and V is the voltage across the capacitor.
From the formula, we can express the charge Q in terms of capacitance C and voltage V:
Q=C⋅V
To determine if C is proportional to Q, we need to consider how C behaves when Q changes. The capacitance C is defined as a constant for a given capacitor, depending on its physical characteristics (like area, distance between plates, and dielectric material).
If we assume that the voltage V across the capacitor changes, then Q will change proportionally with V if C remains constant. This means:
Q \propto V \quad \text{(if C is constant)}
However, C itself does not change with Q; it is a constant for a specific capacitor configuration.
Since C is a constant and does not vary with the charge Q, we conclude that:
C is not proportional to Q.
Thus, we can say that the capacitance C is not proportional to the charge Q.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
65 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
Consider the circuit shown where C1=6μF,C2=3μF and V=20V. Capacitor C1 is first charged by closing the switch S1. Switch S1 is then opened, and the charged capacitor is connected to the uncharged capacitor C2 by closing S2.
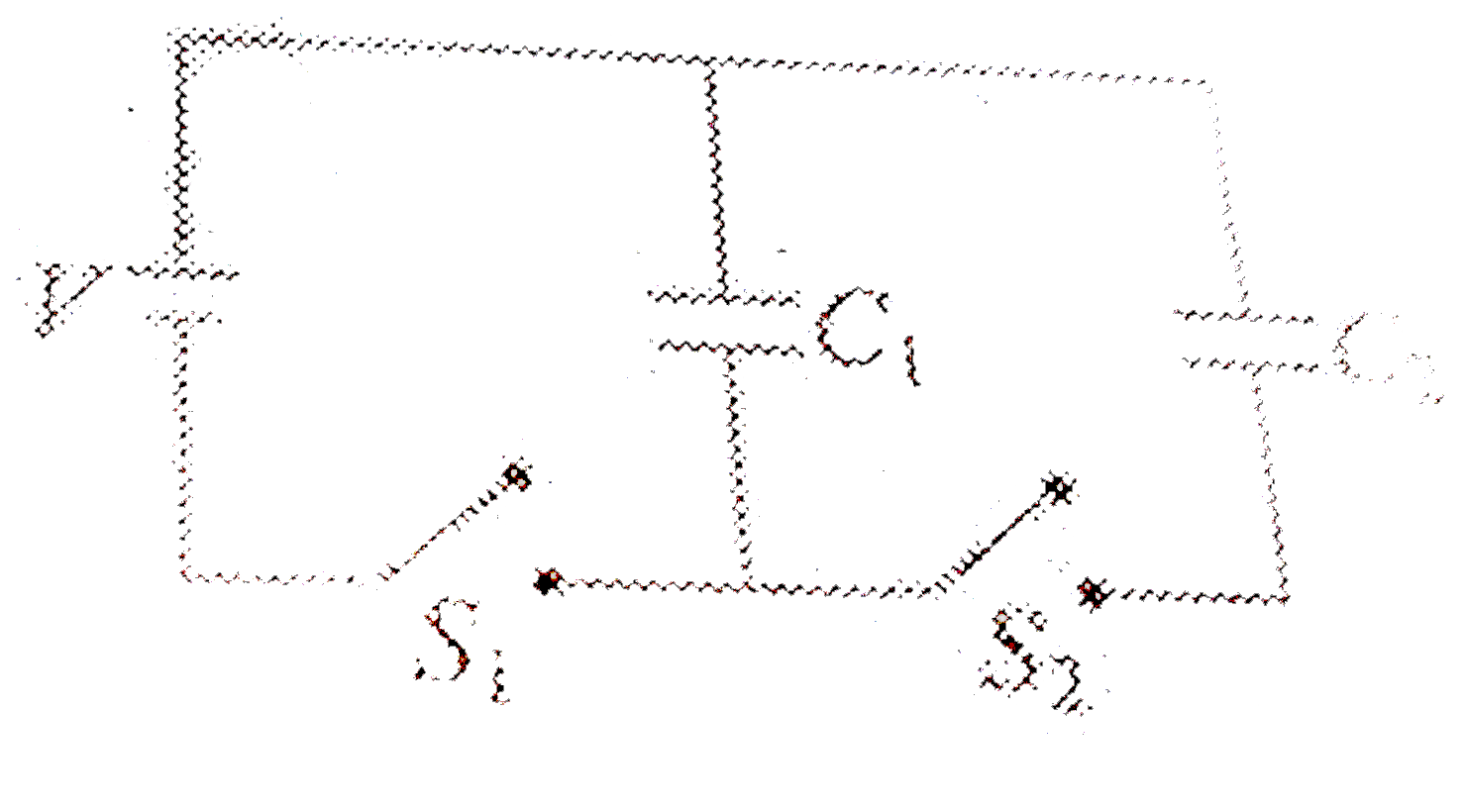
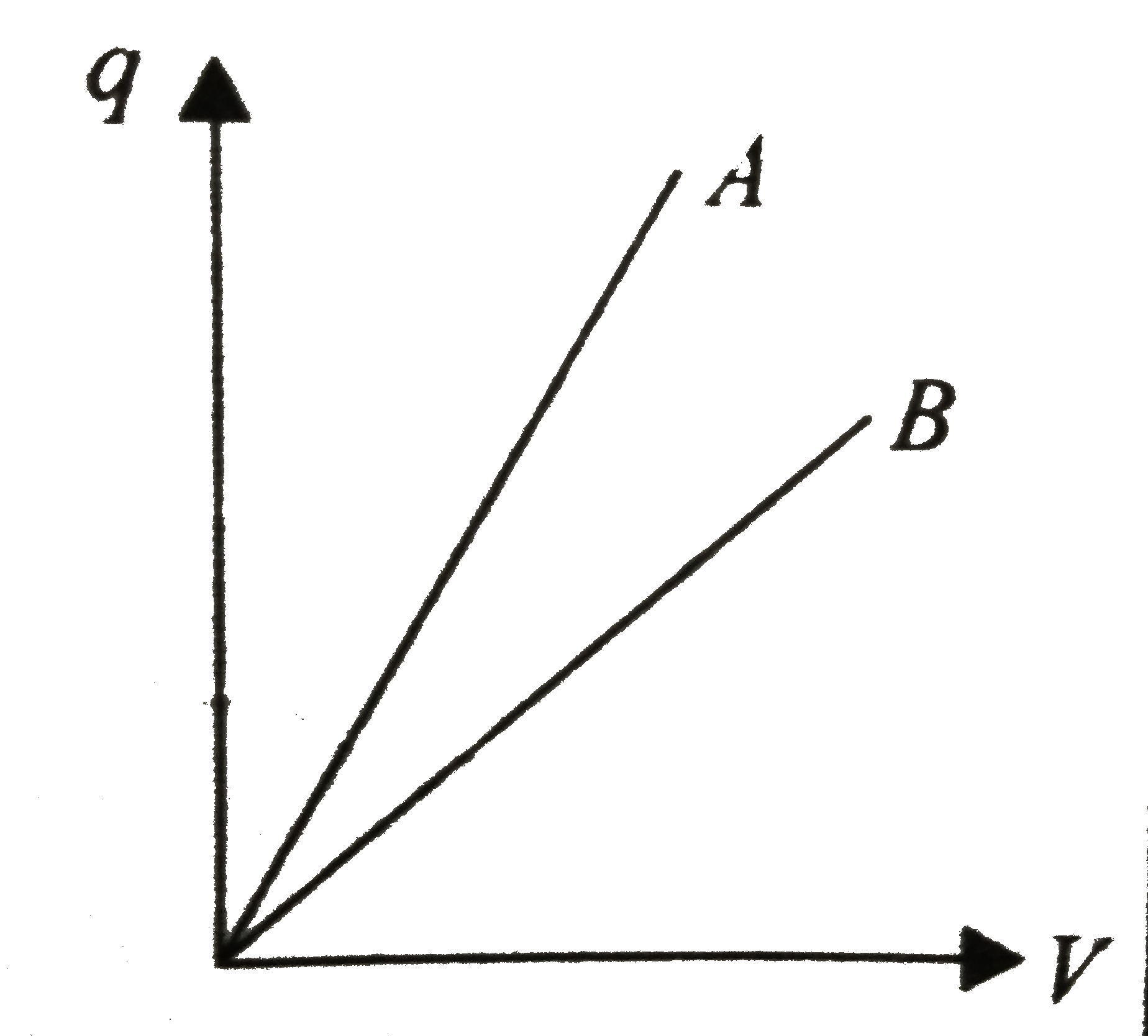
View SolutionThe given graph shows variation of charge .q. versus potential difference .V. for two capacitors

C1andC2. Both the capacitors have same plate separation but plate area of C2 is greater than that of C1. Which line (A or B) corresponds to C1 and why?
View Solution
Knowledge Check
Two identical capacitors 1 and 2 are connected in series to a batery as shown in figure. Capacitor 2 contains a dielectric slab of dieletric constant k as shown. Q1 and Q2 are the charges stored in the capacitors. Now the dielectirc slab us removed and the corresponding charges are Q'1 and Q'2. Then
 AQ'1Q1=K+1KBQ'2Q2=K+12CQ'2Q2=K+12KDQ'1Q1=K2
AQ'1Q1=K+1KBQ'2Q2=K+12CQ'2Q2=K+12KDQ'1Q1=K2
Consider the situation shown in (figure) what are the signs of q1 and q2 ? If the lines are drawn in proportion to the charge, what is the ratio q1q2 ?

View SolutionTwo capacitors of equal capacitance (C1=C2) are as shown in the figure. Initially, while the swithc is open (as shown) one of the capacitors is uncharged and the other carries charge Q0. The energy stored in the charged capacitor is U0. Sometime after the switch is closed, the capacitors C1andC2 carry charged Q1andQ2 respectively, the energy stored in the capacitors are U1andU2 respectively. Which of the following expression is correct?

View SolutionShows these variation of charge q for two capacitors C1 and C2 The two capacitors have the same plate separation. But the plate area of C2 is double than that of C1. Which of the lines in the figure corresponds to C1 and C2 and why?
 .
.
View SolutionConsider a parallel plate capacitor having charge Q. Then,
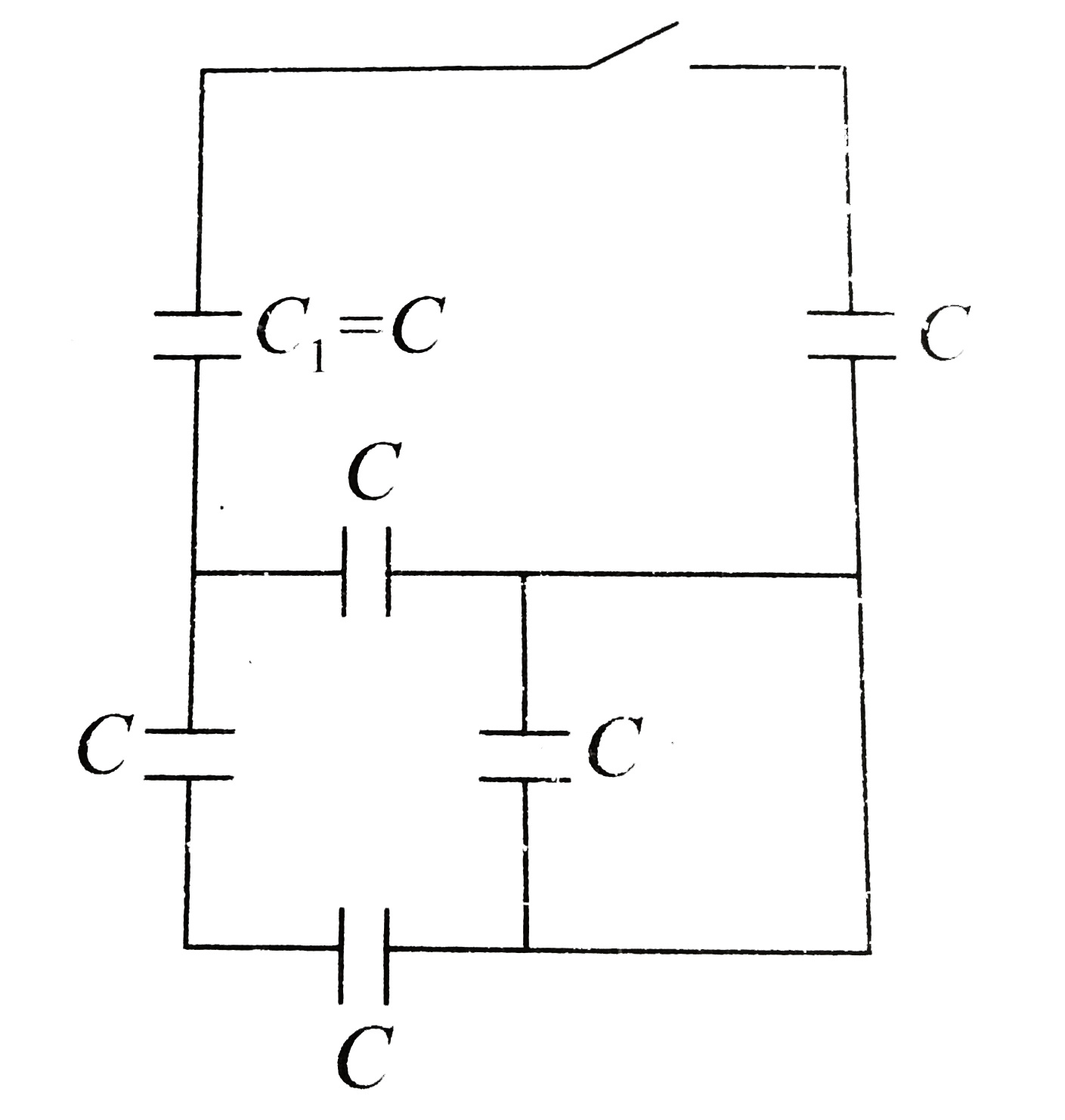
View SolutionIn the circuit shown, all capacitors are identical. Initially, the switch is open and the capacitor marked C1 is the only one charged to a value Q0. After the switch is closed and the equilibrium is reestablished, the charge on the capacitor marked C1 is Q. Find the ratio initial change to final charge in capacitor C1.
View SolutionA dielectric slab is inserted between the plates of a capacitor. The charge on the capacitor is Q and the magnitude of the induced charge on each surface of the dielectric is Q'.
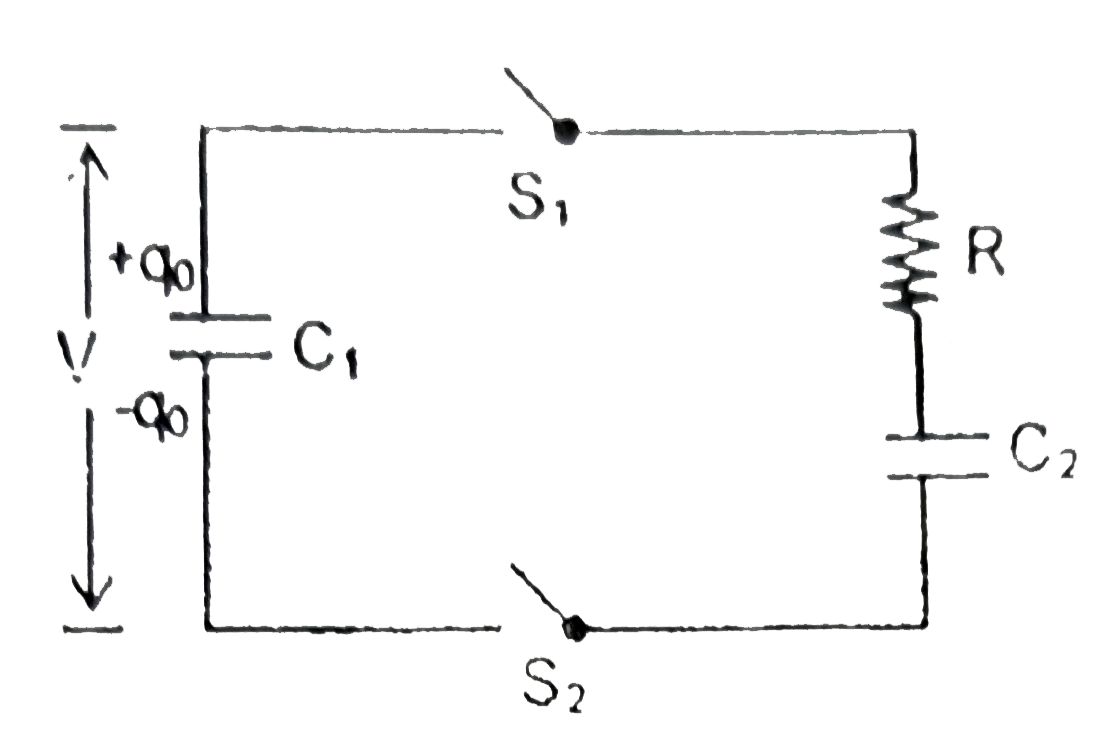
View SolutionThe capacitor C1 in the figure initially carries a charge q0. When the switch S1 and S2 are shut, capacitor C1 is connected in series to a resistor R and a second capacitor C2, which initially does not carry any charge.
If the heat lost in the resistor after a long time of closing the switch is q20C2kC1(C1+C2), then Find the value of k.
View Solution
