Assertion : A conducting rod is placed between boiling water and ice. If rod is broken into two equal parts and two parts are connected side by side, then rate of melting of ice will increase ot four times.
Reason : Thermal resistance will become four times.
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:C
To solve the problem, we need to analyze the assertion and the reason provided in the question regarding the conducting rod placed between boiling water and ice.
Step 1: Understand the Assertion
The assertion states that if a conducting rod is placed between boiling water and ice, and then the rod is broken into two equal parts and connected side by side, the rate of melting of ice will increase by four times.
Step 2: Analyze the Heat Transfer
The rate of heat transfer (dQ/dt) through a conducting rod can be expressed using Fourier's law of heat conduction:
dQdt=k⋅A⋅ΔTL
where:
- k is the thermal conductivity of the material,
- A is the cross-sectional area,
- ΔT is the temperature difference,
- L is the length of the rod.
Step 3: Effect of Breaking the Rod
When the rod is broken into two equal parts:
- The length of each part becomes L/2.
- When connected side by side, the effective area A doubles (i.e., 2A).
Step 4: Calculate the New Rate of Heat Transfer
Substituting the new values into the heat transfer equation:
dQdtnew=k⋅(2A)⋅ΔTL/2
This simplifies to:
dQdtnew=2k⋅A⋅ΔT⋅2L=4⋅k⋅A⋅ΔTL
Thus, the new rate of heat transfer is four times the original rate:
dQdtnew=4⋅dQdtoriginal
Step 5: Conclusion on Melting of Ice
Since the rate of heat transfer to the ice increases by four times, the rate of melting of ice will also increase by four times. Therefore, the assertion is correct.
Step 6: Analyze the Reason
The reason states that thermal resistance will become four times. However, thermal resistance R can be expressed as:
R=Lk⋅A
After breaking the rod:
- The new length is L/2,
- The new area is 2A.
Thus, the new thermal resistance becomes:
Rnew=L/2k⋅(2A)=L4kA
This shows that the thermal resistance actually decreases to one-fourth of the original resistance, not increases.
Final Conclusion
- The assertion is correct: the rate of melting of ice will increase by four times.
- The reason is incorrect: thermal resistance will decrease to one-fourth, not increase.
Answer:
- Assertion: True
- Reason: False
The assertion states that if a conducting rod is placed between boiling water and ice, and then the rod is broken into two equal parts and connected side by side, the rate of melting of ice will increase by four times.
The rate of heat transfer (dQ/dt) through a conducting rod can be expressed using Fourier's law of heat conduction:
dQdt=k⋅A⋅ΔTL
where:
- k is the thermal conductivity of the material,
- A is the cross-sectional area,
- ΔT is the temperature difference,
- L is the length of the rod.
When the rod is broken into two equal parts:
- The length of each part becomes L/2.
- When connected side by side, the effective area A doubles (i.e., 2A).
Substituting the new values into the heat transfer equation:
dQdtnew=k⋅(2A)⋅ΔTL/2
This simplifies to:
dQdtnew=2k⋅A⋅ΔT⋅2L=4⋅k⋅A⋅ΔTL
Thus, the new rate of heat transfer is four times the original rate:
dQdtnew=4⋅dQdtoriginal
Since the rate of heat transfer to the ice increases by four times, the rate of melting of ice will also increase by four times. Therefore, the assertion is correct.
The reason states that thermal resistance will become four times. However, thermal resistance R can be expressed as:
R=Lk⋅A
After breaking the rod:
- The new length is L/2,
- The new area is 2A.
Rnew=L/2k⋅(2A)=L4kA
This shows that the thermal resistance actually decreases to one-fourth of the original resistance, not increases.
- The assertion is correct: the rate of melting of ice will increase by four times.
- The reason is incorrect: thermal resistance will decrease to one-fourth, not increase.
- Assertion: True
- Reason: False
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 1 Objective
11 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 1 Subjective
13 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Exercise 22.2
7 Videos
- BASIC MATHEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
Two containers having boiling water and ice are connected through a conducting metal rod. The whole ice melts in time T. now the rod is cut into two equal parts and both parts are connected in parallel between the containers the time required to melt the same amount of ice will be
View SolutionA wire of resistance 18Ω is divided into three equal parts. These parts are connected as sides of a triangle , the equivalent resistance of any two corners of the triangle will be
View SolutionAssertion : A resistance wire is broken into four pices and all are connected in parallel. Then, net resistance becomes 1/16 times.
Reason : In parallel net resistance is less than the smallest value of individual resistance.
View SolutionTwo identical rods are connected between two containers. One of them is at 100∘C containing water and another is at 0∘C containing ice. If rods are connected in parallel then the rate of melting of ice is q1g/s . If they are connected in series then teh rate is q2g/s . The ratio q2/q1 is
View SolutionTwo identical conducting rods are first connected independently to two vessels, one containing water at 100∘C and the other containing ice at 0∘C. In the second case, the rods are joined end to end connected to the same vessels. Let m1andm2 g/s be the rate of melting of ice in the two cases respectively, the ratio m1m2 is
View SolutionA metal rod AB of length 10x has it one end in ice at 0∘C and the other end B in water at 100∘C If a point P on the rod is maintained at 400∘C then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of melting of ice is 80cal/g If the point P is at a distance of λx from the ice end A find the value of λ [neglect any heat loss to the surrounding] .
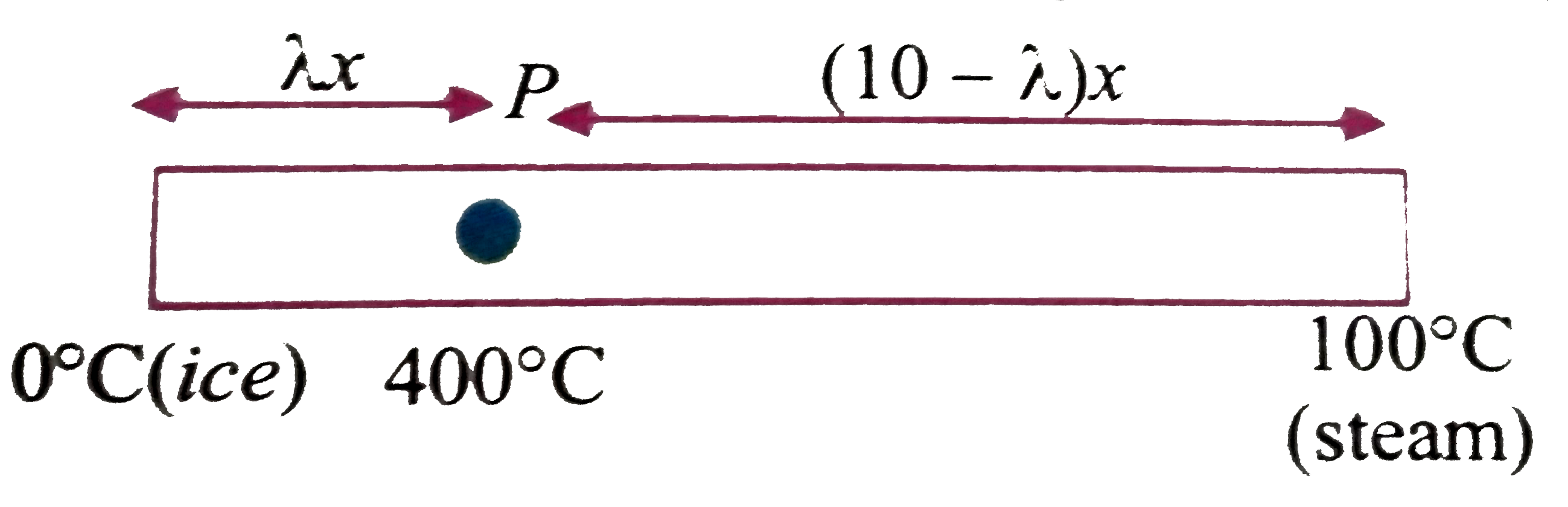 .
.
View SolutionAn ice ball of radius a and mass m is placed at 0∘C inside a thick hollow sphere of inner and outer radii a and b whose thermal conductivity varies as k=αr2, where α is a positive constant and r is the distance from centre. The temperature of surrounding is θ0 and latent heat of fusion for ice is Lf. Then , time required to completely melt the ice ball is (Neglect the contraction in volume when ice melts into water and any change in thermal resistance due to melting of ice of the system.)
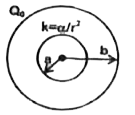
View SolutionTwo identical conducting rods are first connected independently to two vessels, one containing water at 100∘C and the other containing ice at 0∘C. In the second case, the rods are joined end to end and connected to the same vessels. Let q1andq2 gram per second be the rate of melting of ice in the two cases respectively. The ratio q1q2 is
(a) 12 (b)21 (c)41 (d)14
View SolutionChoose the correct option:
Two identical conducting rods are first connected independently to two vessels, one containing water at 100∘C and the other containing ice at 0∘C. In the second case, the rods are joined end to end and connected to the same vessels. Let q1andq2 gram per second be the rate of melting of ice in the two cases respectively. The ratio q1q2 is:
View SolutionTwo identical conducting rods are first connected independently to two vessels, one containing water at 100∘C and the other containing ice at 0∘C. In the second case, the rods are joined end to end and connected to the same vessels. Let q1andq2 gram per second be the rate of melting of ice in the two cases respectively. The ratio q1q2 is
(a) 12 (b)21 (c)41 (d)14
View Solution
