Assertion : A spring block system is kept over a smooth surface as shown in figure. If a constant horizontal force F is applied on the block it will start oscillating simple harmonically.
Reason : Time period of oscillation is less then 2π√mk.
Both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
Both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
Assertion is true, but the Reason is false.
Assertion is false but the Reason is true.
The correct Answer is:C
To solve the question, we need to analyze both the assertion and the reason provided.
1. Understanding the Assertion:
- The assertion states that a spring-block system on a smooth surface will oscillate harmonically when a constant horizontal force F is applied.
- Since the surface is smooth, we can ignore friction. The spring will stretch due to the applied force until it reaches a new equilibrium position.
2. Equilibrium Position:
- When the force F is applied, the spring stretches by a distance x0 from its natural length.
- At this new equilibrium position, the force exerted by the spring (Fs) is equal to the applied force F. Thus, we have:
F=k⋅x0
- This indicates that the system is in equilibrium at this position.
3. Displacement from Equilibrium:
- If the block is displaced from this equilibrium position by a distance x, the spring will exert a restoring force.
- The net force acting on the block when displaced is:
F′=F−k(x+x0)
- Substituting F=k⋅x0 into the equation gives:
F′=k⋅x0−k(x+x0)=−k⋅x
- This shows that the net force is proportional to the displacement x and acts in the opposite direction, indicating simple harmonic motion.
4. Equation of Motion:
- According to Newton's second law, we can express the net force as:
F′=m⋅a=−k⋅x
- This leads to the equation:
a=−km⋅x
- This is the standard form of simple harmonic motion, confirming that the assertion is true.
5. Analyzing the Reason:
- The reason states that the time period of oscillation is less than 2π√mk.
- The time period T for a simple harmonic oscillator is given by:
T=2π√mk
- This indicates that the time period is exactly 2π√mk, not less than it. Therefore, the reason is false.
6. Conclusion:
- The assertion is true, and the reason is false. Thus, the correct option is that the assertion is true, but the reason is false.
Final Answer:
The assertion is true, and the reason is false.
- The assertion states that a spring-block system on a smooth surface will oscillate harmonically when a constant horizontal force F is applied.
- Since the surface is smooth, we can ignore friction. The spring will stretch due to the applied force until it reaches a new equilibrium position.
- When the force F is applied, the spring stretches by a distance x0 from its natural length.
- At this new equilibrium position, the force exerted by the spring (Fs) is equal to the applied force F. Thus, we have:
F=k⋅x0
- This indicates that the system is in equilibrium at this position.
- If the block is displaced from this equilibrium position by a distance x, the spring will exert a restoring force.
- The net force acting on the block when displaced is:
F′=F−k(x+x0)
- Substituting F=k⋅x0 into the equation gives:
F′=k⋅x0−k(x+x0)=−k⋅x
- This shows that the net force is proportional to the displacement x and acts in the opposite direction, indicating simple harmonic motion.
- According to Newton's second law, we can express the net force as:
F′=m⋅a=−k⋅x
- This leads to the equation:
a=−km⋅x
- This is the standard form of simple harmonic motion, confirming that the assertion is true.
- The reason states that the time period of oscillation is less than 2π√mk.
- The time period T for a simple harmonic oscillator is given by:
T=2π√mk
- This indicates that the time period is exactly 2π√mk, not less than it. Therefore, the reason is false.
- The assertion is true, and the reason is false. Thus, the correct option is that the assertion is true, but the reason is false.
The assertion is true, and the reason is false.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Miscellaneous Examples
8 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A block of mass 10 kg is kept over a rough surface and a force F=4t is applied on it. At what value of t the block will start moving :-
View SolutionA body of mass m attached to one end of an ideal spring of force constant k is executing simple harmonic motion. Establish that the time - period of oscillation is T=2π√m/k.
View SolutionA block of mass'm' it kept over the smooth surface of the plank of mass M. the plank of length l is kept over the smooth horizontal surface. A constant horizontal force F is applied onto the plank as shown in figure. Calculate the time after which the block falls off the plank?

View SolutionA system is shown in the figure. The force The time period for small oscillations of the two blocks will be

View Solution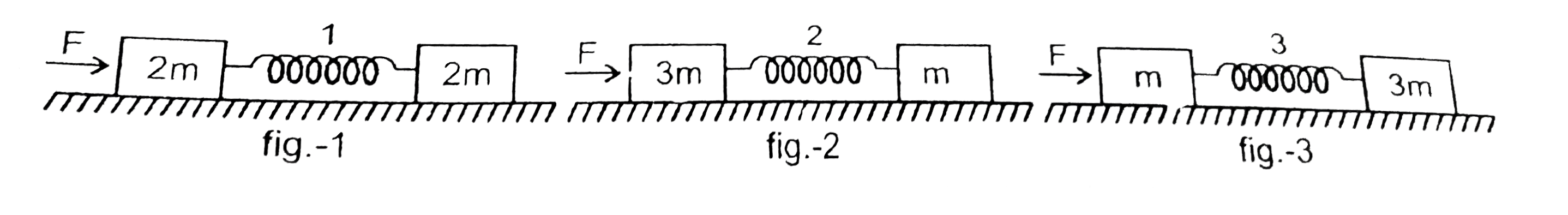
In each of three figure shown, two blocks are connected by a light spring and the system is placed on smooth horizontal surface. A constant horizontal force of magnitude F is applied to left block as shown. Assuming spring constant in all three cases to be same, which of the following statements is/are true.
View SolutionIn each of three figures shown, two blocks are connected by a light spring and the system is placed on smooth horizontal surface. A constant horizontal force of magnitude F is applied to left block as shown. Assuming spring constant in all three cases to be same, which of the following statement is/are ture.
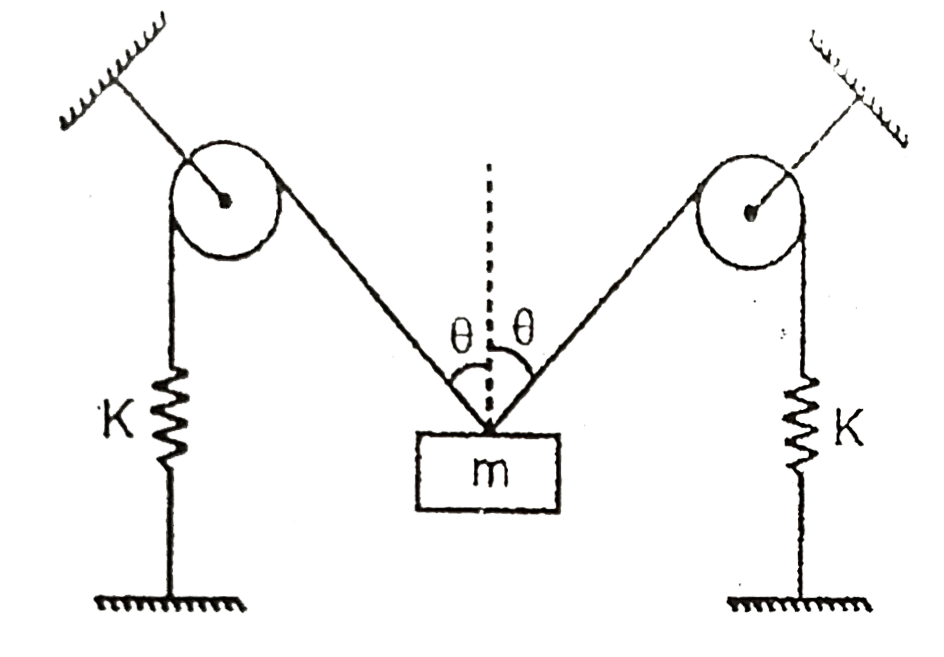
View SolutionIn the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
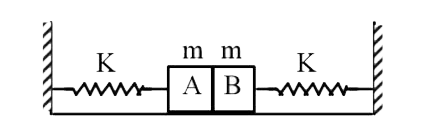
View SolutionTwo blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA spring-block system undergoes vertical oscillations above a large horizontal metal sheet with uniform positive charge. The time period of the oscillations is T. If the block is given a charge Q, its time period of oscillation will be
View Solution
