Assertion : A uniform disc of radius R is performing impure rolling motion on a rough horizontal plane as shown in figur. After some time the disc comes to rest. It is possible only when v0=ω0R2

Reason : For a body performing pure rolling motion, the angular momentum uis conserved about any point in space.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is fasle
If Assertion is false but Reason is true
The correct Answer is:C
Angular momentum about bottommost point will be
L=mv0R−12mR2ω0
If L=0orv0=ω0R2, disc will come to rest after some time.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (A) Chapter Exercises
83 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
An object of mass M and radius R is performing pure rolling motion on a smooth horizontal surface under the action of a constant force F as shown in Fig. The object may be

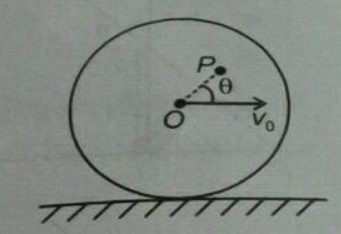
View SolutionA uniform disc of radius R is in pure rolling on a fixed horizontal surface with constant speed v0 as shown in the figure. For what value of θ, speed of point P will be v02√(5+2√3) ? (OP= R/2 and O is the centre of disc)
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
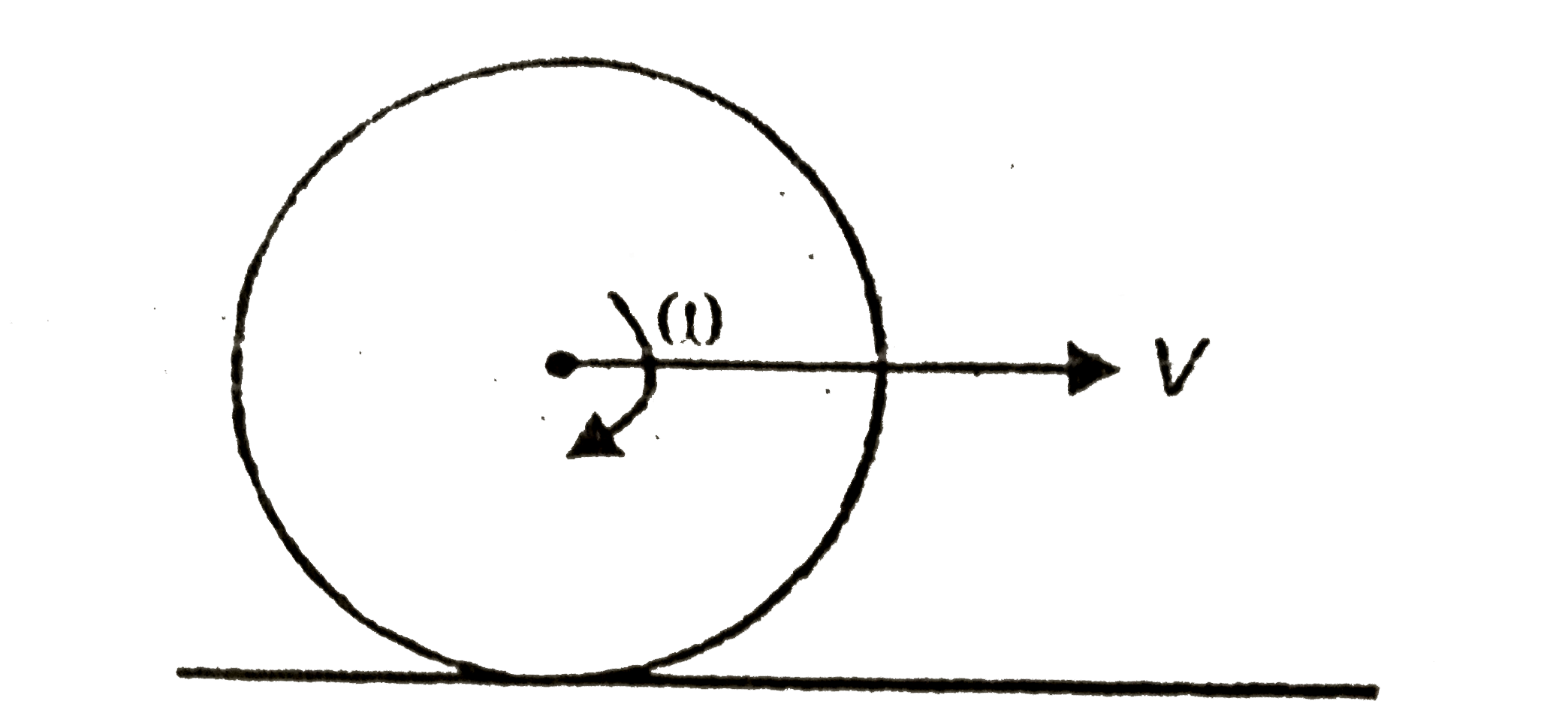
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.
View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

View Solutiona uniform circular disc of radiu8s r placed on a roughn horizontal plane has initial velocity v0 and an angul,ar velocity ω0 has shown The disc comes to rest after moving some distance in the direction of motion. Then

View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

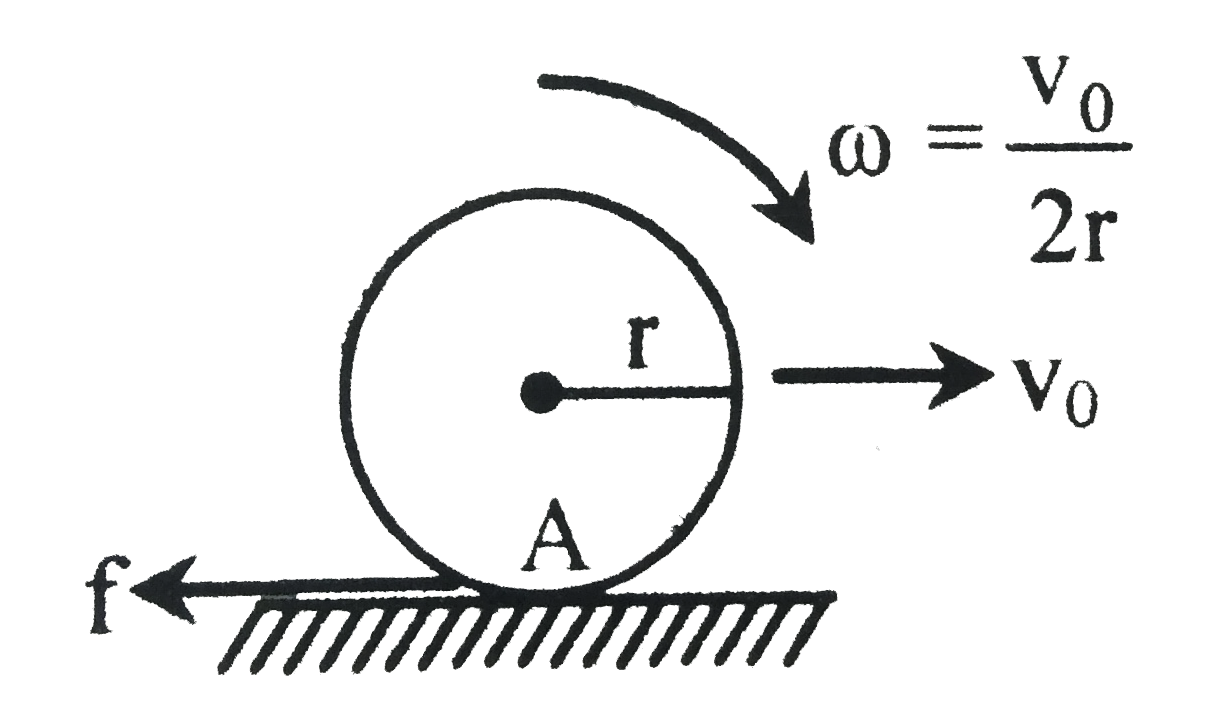
View SolutionA sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
 .
.
View SolutionA particle of mass 'm' is attached to the rim of a uniform disc of mass 'm' and radius R. The disc is rolling wihtout slipping on a stationery horizontal surface as shown in the figure. At a particular instant, the particle is at the topmost position and centre of the disc has speed v0 amd its angular speed is ω. Choose the correct option (s).
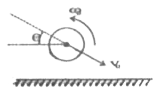
View SolutionA solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
View Solution
