Assertion : For small deformations, the stress and strain are proportional to each other.
Reason: A class of solids called elastomers does not obey Hooke's law.
Both assertion and reason are true and reason is the correct explanation of assertion.
Both assertion and reason are true but reason is not the correct explanation of assertion.
Assertion is true but reason is false.
Both assertion and reason are false.
The correct Answer is:B
To solve the given question, we need to analyze both the assertion and the reason provided.
Step 1: Analyze the Assertion
The assertion states: "For small deformations, the stress and strain are proportional to each other."
- This statement is true and is derived from Hooke's Law, which states that within the elastic limit of a material, the stress applied to it is directly proportional to the strain produced. Mathematically, this can be expressed as:
σ=E⋅ϵ
where σ is the stress, E is the modulus of elasticity, and ϵ is the strain.
Step 2: Analyze the Reason
The reason states: "A class of solids called elastomers does not obey Hooke's law."
- This statement is also true. Elastomers are materials that exhibit significant elastic deformation when a small amount of stress is applied. Unlike materials that obey Hooke's law, elastomers can experience large strains for relatively small stresses, indicating that they do not maintain a linear relationship between stress and strain.
Step 3: Determine the Relationship Between Assertion and Reason
Now, we need to determine if the reason provided is a correct explanation for the assertion.
- Although both the assertion and the reason are true, the reason does not explain why stress and strain are proportional for small deformations. Instead, it highlights an exception (elastomers) to the general rule (Hooke's law). Therefore, the reason does not serve as a correct explanation for the assertion.
Conclusion
Based on the analysis:
- The assertion is true.
- The reason is true but does not explain the assertion.
- Thus, the correct option is: Both assertion and reason are true, but reason is not the correct explanation of assertion.
Final Answer
Option B: Both assertion and reason are true, but reason is not the correct explanation of assertion.
---
The assertion states: "For small deformations, the stress and strain are proportional to each other."
σ=E⋅ϵ
where σ is the stress, E is the modulus of elasticity, and ϵ is the strain.
The reason states: "A class of solids called elastomers does not obey Hooke's law."
Now, we need to determine if the reason provided is a correct explanation for the assertion.
Based on the analysis:
- The assertion is true.
- The reason is true but does not explain the assertion.
- Thus, the correct option is: Both assertion and reason are true, but reason is not the correct explanation of assertion.
Option B: Both assertion and reason are true, but reason is not the correct explanation of assertion.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Hooke'S Law
3 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Higher Order Thinking Skills
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - NCERT
8 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Assertion: Ratio of stress and strain is always constant for a substance.
Reason : This ratio is called modulus of elasticity .
View SolutionAssertion Upto elastic limit of a stress-strain curve, the steel wire tends to regain its original shape when stress is removed.
Reason Within elastic limit, the wire follows Hooke's law.
View SolutionAssertion (A): Centripetal force does no work .
Reason (R) : Force and displacement are perpendicular to each other
View SolutionAssertion:- Materials can be stretched even beyond proportionality limit. (point till which Hooke's law is valid is called proportionality limit)
Reason:- Elastic forces can be conservative even beyond proportional limit.
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
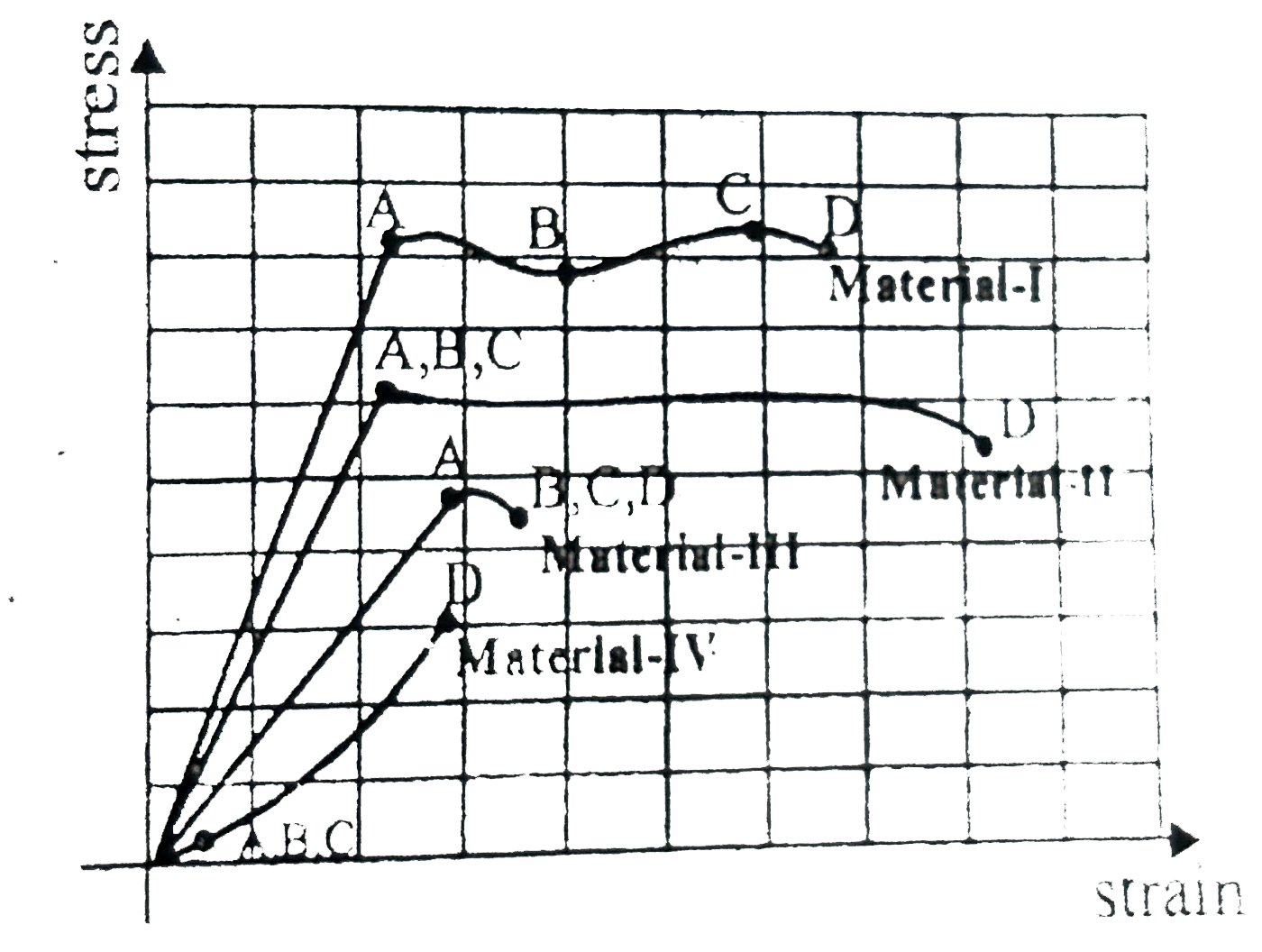
Material which is good for making wires by stretching is
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe is
View SolutionAssertion : The materials which have very small range of plastic extension are called brittle material.
Reason: If the stress is increased beyond the elastic limit, the material will break.
View SolutionAssertion When two magnets are brought closer to each other, then they will always repel each other.
Reason According to Lanz's law induced effects always opposes the cause.
View Solution
