Assertion:- Materials can be stretched even beyond proportionality limit. (point till which Hooke's law is valid is called proportionality limit)
Reason:- Elastic forces can be conservative even beyond proportional limit.
Both Assertion and Reason are correct and Reason is the correct explanation for Assertion
Both Assertion and Reason are correct but Reason is not the correct explanation for Assertion
Assertion is correct but Reason is wrong
Both Assertion and Reason are wrong
The correct Answer is:A
To solve the given assertion-reason question, we will analyze both the assertion and the reason separately.
1. Understanding the Assertion:
- The assertion states that materials can be stretched even beyond the proportionality limit. The proportionality limit is the point up to which Hooke's law is valid, meaning that stress is directly proportional to strain.
- Conclusion: This assertion is true. Materials can indeed be stretched beyond the proportionality limit, although they may not obey Hooke's law in that region.
2. Understanding the Reason:
- The reason states that elastic forces can be conservative even beyond the proportionality limit. A conservative force is one where the work done in moving an object between two points is independent of the path taken.
- Analysis: When a material is stretched beyond the proportionality limit, it may exhibit plastic deformation, where the material does not return to its original shape. In such cases, the work done is not recoverable, indicating that the elastic forces are not conservative.
- Conclusion: This reason is false. Elastic forces do not remain conservative beyond the proportionality limit.
3. Final Evaluation:
- Since the assertion is true and the reason is false, the correct option for this assertion-reason question is that the assertion is correct but the reason is incorrect.
Final Answer:
The assertion is true, but the reason is false.
- The assertion states that materials can be stretched even beyond the proportionality limit. The proportionality limit is the point up to which Hooke's law is valid, meaning that stress is directly proportional to strain.
- Conclusion: This assertion is true. Materials can indeed be stretched beyond the proportionality limit, although they may not obey Hooke's law in that region.
- The reason states that elastic forces can be conservative even beyond the proportionality limit. A conservative force is one where the work done in moving an object between two points is independent of the path taken.
- Analysis: When a material is stretched beyond the proportionality limit, it may exhibit plastic deformation, where the material does not return to its original shape. In such cases, the work done is not recoverable, indicating that the elastic forces are not conservative.
- Conclusion: This reason is false. Elastic forces do not remain conservative beyond the proportionality limit.
- Since the assertion is true and the reason is false, the correct option for this assertion-reason question is that the assertion is correct but the reason is incorrect.
The assertion is true, but the reason is false.
Topper's Solved these Questions
Similar Questions
The stress strain graph for a metal wire is shown in the fig. Up to the point E, the wire returns to its original state O along the curve EPO, when it is gradually unloaded. Point B corresponds to the fracture of the wire.
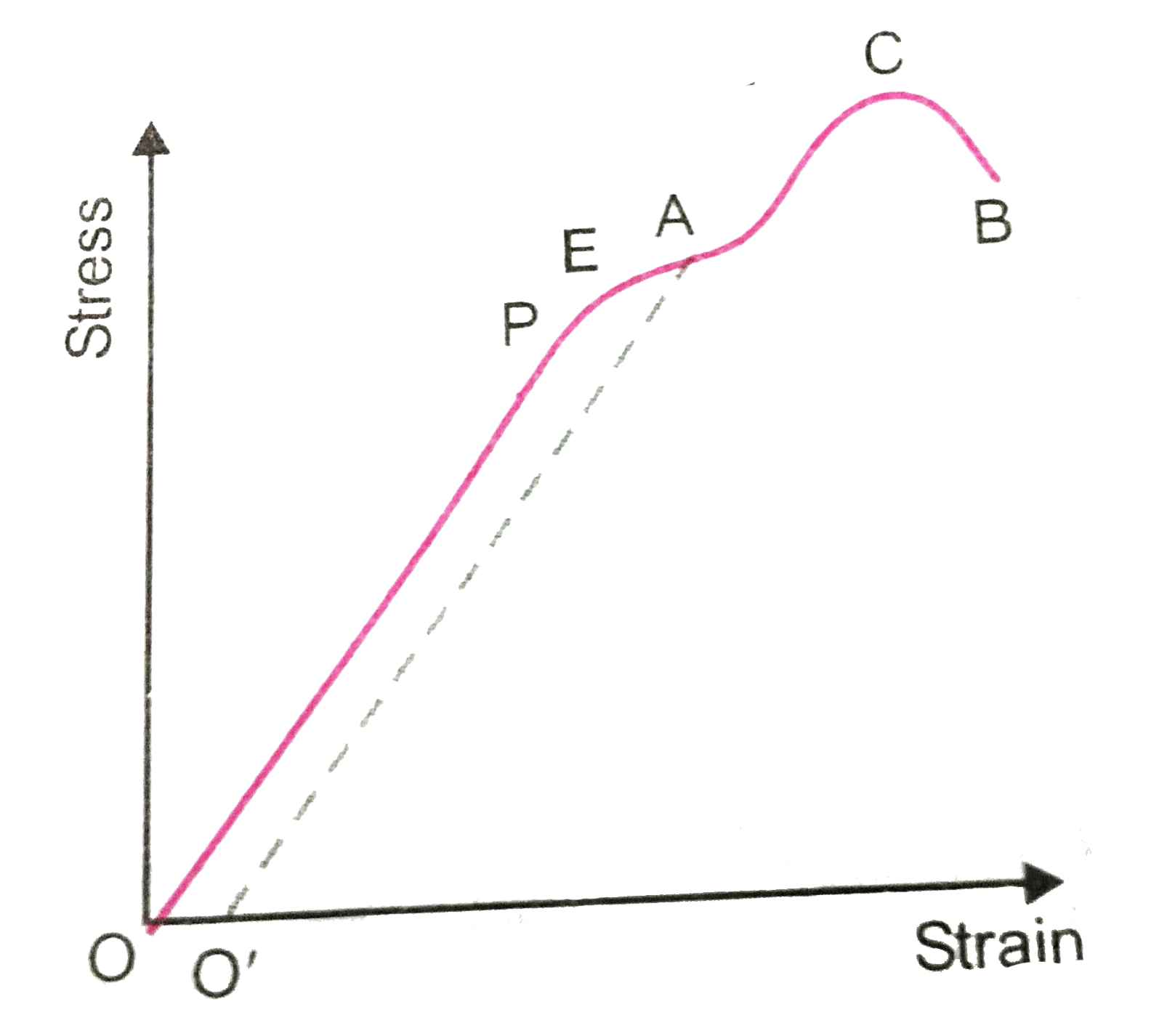
(a) Up to what point on the curve is Hooke's law obeyed? (this point some times called proportional limits).
(b) Which point on the curve corresponding to elastic limit or yield point of the wire?
(c ) Indicate the elastic and plastic regions of the stress-strain graph.
(d) Describe what happens when the wire is loaded up to a stress corresponding to the point A on the graph and then unloaded gradually. In particular explain the dotted curve.
(e) What is peculiar about the portion of the stress- strain graph from C to B? Up to what stress can the wire be subjected without causing fracture?View SolutionA steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is x. Strain in the wire is proportional to
View Solution
Knowledge Check
- Question 1 - Select One
Assertion: The reactant which is present in large amount limits the amount of product formed is called limiting reagent.
Reason : Amount of product formed does not depend upon the amount of reactants taken.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
Figure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
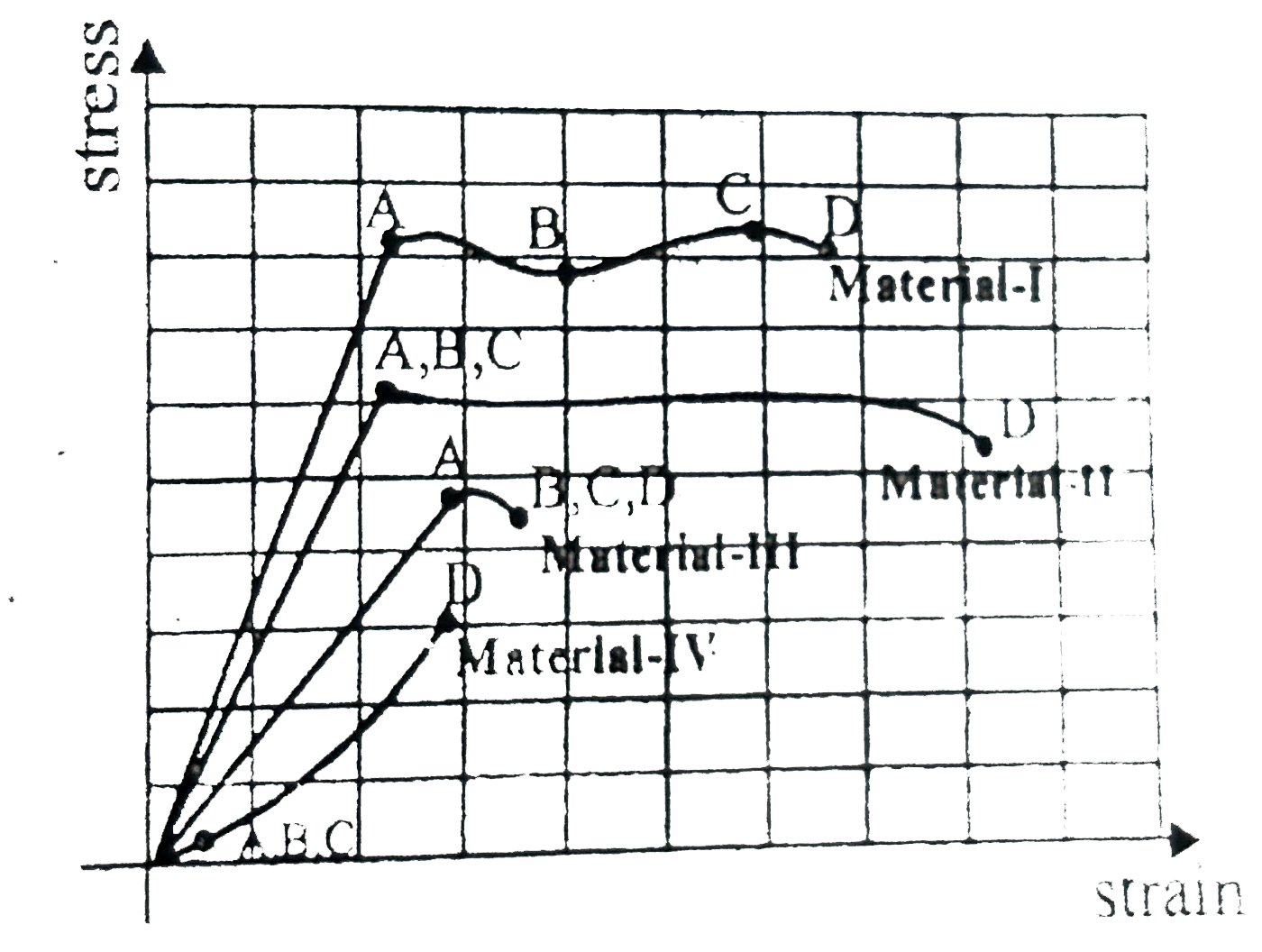
Material which is good for making wires by stretching isView SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe isView SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe isView SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.

Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.

If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe isView SolutionWhen a tensile or compressive load 'P' is applied to rod or cable, its length changes. The change length x which, for an elastic material is proportional to the force Hook' law).
Pαx or P=kx
The above equation is similar to the equation of spring. For a rod of length L, area A and young modulue Y. the extension xcan be expressed as.
x=PLAY or P=AYx, hence K=AYL
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called strain energy & equal to 12Px. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by energy conservation.
In above problem if mass of 10kg falls on the massless collar attached to rod from the height of 99cm then maximum extension in the rod is equal (rod of length 4m, area 4cm2 and young modules 2×1010N/m2 g=10m/sec2)-View SolutionAssertion: Kepler's second law can be understood by conservation of angular momentum principle.
Reason: Kepler's second law is related with areal velocity which can further be proved to be used on coservation of angular momentum as (dA/dt)=(r2ω)/2.View SolutionWhen a tensile or compressive load 'P' is applied to rod or cable, its length changes. The change length x which, for an elastic material is proportional to the force Hook' law).
Pαx or P=kx
The above equation is similar to the equation of spring. For a rod of length L, area A and young modulue Y. the extension xcan be expressed as.
x=PLAY or P=AYx, hence K=AYL
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called stra energy & equal to 12Px. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by enerfy conservation.
It two rods of same length (4m) and cross section areas 2cm2 and 4cm2 with same young modulus 2×1010N/m2 are attached one after the other with mass 600kg then angular frequency is-View Solution

