Assertion: In case of charged spherical shells, E-r graph is discontinuous while V-r graph is continuous
Reason: According to Gauss's theorem only the charge inside a closed surface can produce electric field at some point.
If both Assertion and Reason are true but Reason is the correct explanation of Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:C
To solve the question, we need to analyze the assertion and the reason provided, and then determine their validity based on the principles of electrostatics, particularly focusing on charged spherical shells.
1. Understanding the Assertion:
- The assertion states that in the case of charged spherical shells, the electric field (E) versus radius (r) graph is discontinuous, while the potential (V) versus radius (r) graph is continuous.
- For a charged spherical shell, inside the shell (r < R, where R is the radius of the shell), the electric field is zero. Outside the shell (r > R), the electric field behaves as if all the charge were concentrated at the center (E = kQ/r²).
- Thus, the electric field graph shows a jump from 0 (inside) to kQ/R² (on the surface) and then follows the kQ/r² curve outside, indicating a discontinuity at r = R.
2. Analyzing the Potential:
- The electric potential inside the shell remains constant (V = kQ/R) since the electric field is zero. At the surface, the potential is also kQ/R, and outside the shell, it decreases as V = kQ/r.
- Therefore, the potential graph is continuous across the boundary at r = R, as it does not have a jump; it remains constant inside and matches the value at the surface.
3. Understanding the Reason:
- The reason states that according to Gauss's theorem, only the charge inside a closed surface can produce an electric field at some point.
- This statement is partially true but misleading. While it is correct that only the enclosed charge contributes to the electric field at a point inside the Gaussian surface, charges outside the surface can still influence the electric field at points outside the surface.
4. Conclusion:
- The assertion is true because the E-r graph is indeed discontinuous while the V-r graph is continuous.
- The reason is false because it incorrectly implies that charges outside a closed surface cannot produce an electric field at points outside that surface.
Final Answer:
- The assertion is true, and the reason is false.
- The assertion states that in the case of charged spherical shells, the electric field (E) versus radius (r) graph is discontinuous, while the potential (V) versus radius (r) graph is continuous.
- For a charged spherical shell, inside the shell (r < R, where R is the radius of the shell), the electric field is zero. Outside the shell (r > R), the electric field behaves as if all the charge were concentrated at the center (E = kQ/r²).
- Thus, the electric field graph shows a jump from 0 (inside) to kQ/R² (on the surface) and then follows the kQ/r² curve outside, indicating a discontinuity at r = R.
- The electric potential inside the shell remains constant (V = kQ/R) since the electric field is zero. At the surface, the potential is also kQ/R, and outside the shell, it decreases as V = kQ/r.
- Therefore, the potential graph is continuous across the boundary at r = R, as it does not have a jump; it remains constant inside and matches the value at the surface.
- The reason states that according to Gauss's theorem, only the charge inside a closed surface can produce an electric field at some point.
- This statement is partially true but misleading. While it is correct that only the enclosed charge contributes to the electric field at a point inside the Gaussian surface, charges outside the surface can still influence the electric field at points outside the surface.
- The assertion is true because the E-r graph is indeed discontinuous while the V-r graph is continuous.
- The reason is false because it incorrectly implies that charges outside a closed surface cannot produce an electric field at points outside that surface.
- The assertion is true, and the reason is false.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Objective82videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective15videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.72videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
Assertion : With the help of Gauss's theorm we can find electric field at any point.
Reason : Gauss's theorem can be applied for any type of charge distribution.View SolutionDraw E-r and V-r graphs due to two charged spherical shells as shown in figure (along the line between C and ∝)
 View Solution
View SolutionAssertion: Basic difference between an electric line and magnetic line of force is that former is discontinuous and the latter is continuous or endless.
Reason: No electric lines of force exist inside a charged body but magnetic lines do exist inside a magnet.View SolutionThe electric field inside a spherical shell of uniform surface charge density is
View SolutionAssertion: Gauss's theroem can be applied only for a closed surface.
Reason: Electric flux can be obtained passing from an open surface also.View SolutionIn the following question a statement of assertion (A) is followed by a statement of reason (R )
A: the potential difference between two concentric sphereical shells depends only on the charge of inner shell
R : the electric field in the region in between two shells depedns on the charge of inner shell and electric field is the negative of potential gradient.View Solution(A): A point charge is lying at the centre of a cube of each side. The electric flux emanating from each surface of the cube is 1th6 total flux.
(R ): According to Gauss theorem, total electric flux through a closed surface enclosing a charge is equal to 1/ε0 times the magnitude of the charge enclosed.View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
A Gaussian surface encloses two of the four positively charged particles. The particles that contribute to the electric field at a point P on the surface are
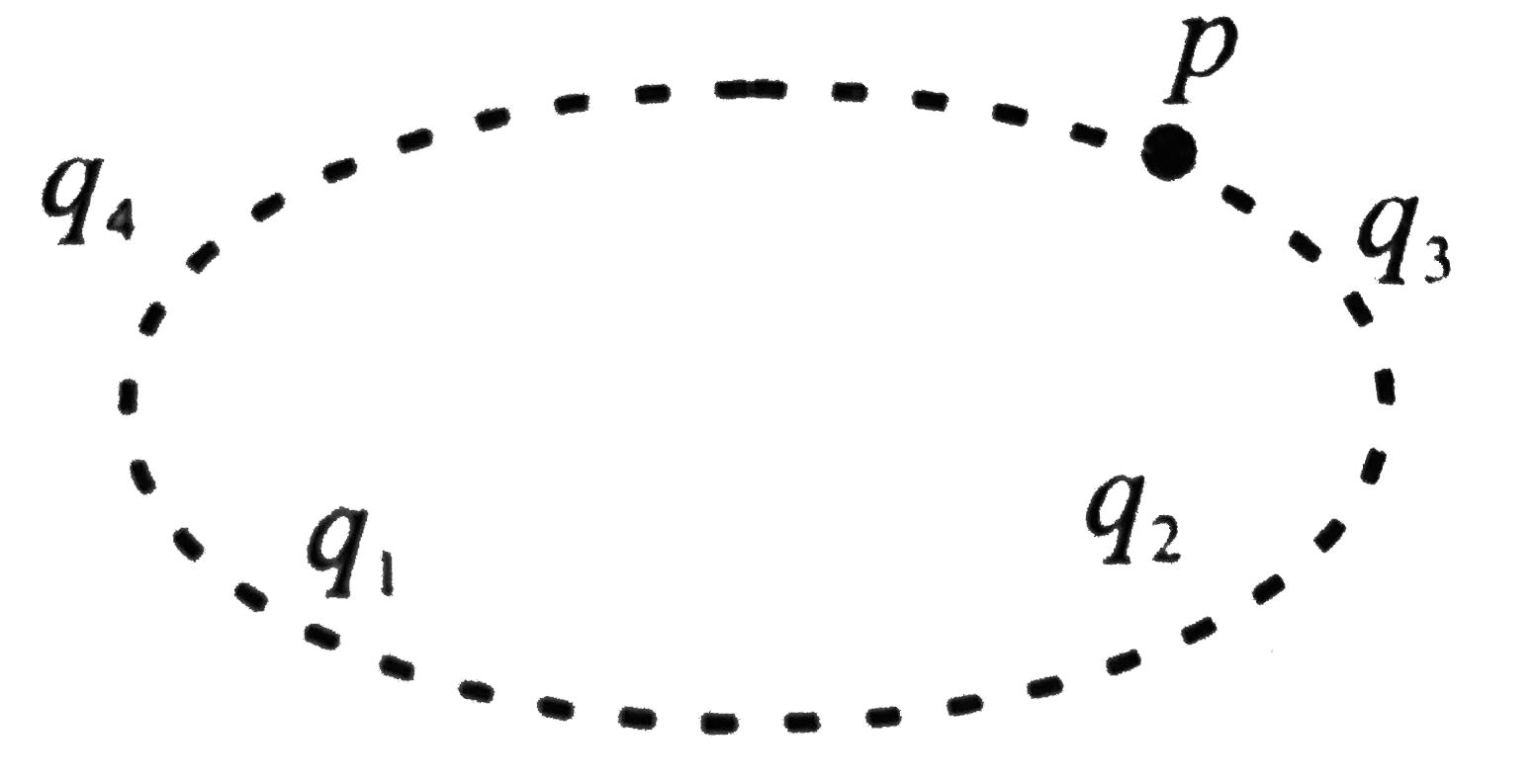 View Solution
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when qencl is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
The net flux of the electric field through the surface isView Solution
