Assertion: In forced oscillations, th steady state motion of the particle is simpl harmonic.
Reason: The frequency of particle after the free oscillations die out, is the natural frequency of the particle.
If both assertion and reson are true and reason is the correct explanation of assertion
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If both assertion and reason are false.
The correct Answer is:C
In forced oscillations, the frequency of particle after free oscillations die out, is the frequency of the driving force, not the natural frequency of the particle.
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTIPSCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
1 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion And Reason
15 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTIPSCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
Knowledge Check
The frequency of the simple harmonic motion attained in forced oscillations, after the forced oscillation die out, is
Athe natural frequency of the particleBthe frequency of the driving forceCdouble the frequency of the driving forceDdouble the natural frequency of the particleIn forced oscillations , a particle oscillates simple harmonically with a frequency equal to
Afrequency of driving forceBnatural frequency of bodyCdiffernece of frequency of driving force and natrual frequencyDmean of frequency of driving force and natural frequencyWhen a particle executes SHM oscillates with a frequency v, then the kinetic energy of the particle
Achange periodically with a frequency of vBchanges periodically with a frequency of 2vCchanges periodically with a frequency of v/2Dremain constant
The acceleration-displacement graph of a particle executing simple harmonic motion is shown in the figure. The frequency of oscillation is
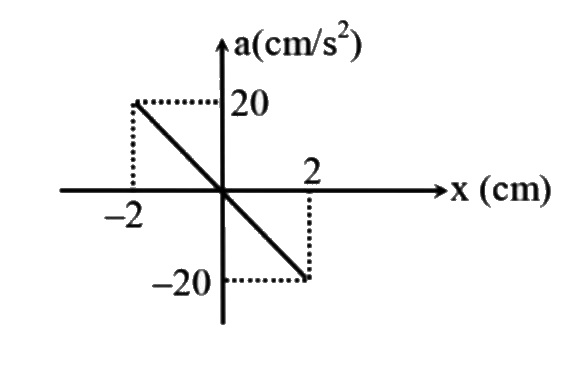
View SolutionThe acceleration-displacement graph of a particle executing simple harmonic motion is shown in the figure. The frequency of oscillation is

View SolutionA particle undergoes simple harmonic motion having time period T. The time taken in 3/8th oscillation is
View SolutionIf the period of oscillation of particle performing simple harmonic motion is 8 s, than the frequency of its kinetic energy will be
View SolutionA particle undergoes simple harmonic motion having time period T. The time taken in 3/8th oscillation is
View Solution
