Assertion : In spring block system if length of spring and mass of block both are halved, then angular frequency of oscillations will remain unchanged.
Reason : Angular frequency is given by ω=√km .
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:D
To solve the question, we need to analyze both the assertion and the reason provided.
1. Understanding the Assertion:
The assertion states that if the length of the spring and the mass of the block are both halved, the angular frequency of oscillations will remain unchanged.
2. Understanding the Reason:
The reason provided states that the angular frequency (ω) is given by the formula:
ω=√km
where k is the spring constant and m is the mass of the block.
3. Analyzing the Effect of Halving the Mass:
If the mass m is halved, we have:
m′=m2
4. Analyzing the Effect of Halving the Length of the Spring:
The spring constant k is inversely proportional to the length of the spring. If the length L is halved, the new spring constant k′ will be:
k′=2k
(because k∝1L)
5. Calculating the New Angular Frequency:
Now, substituting k′ and m′ into the angular frequency formula:
ω′=√k′m′=√2km2=√2k⋅2m=√4km=2√km=2ω
This shows that the new angular frequency ω′ is actually twice the original angular frequency ω.
6. Conclusion:
Since the new angular frequency is 2ω, the assertion that the angular frequency remains unchanged is incorrect. However, the reason provided about the formula for angular frequency is correct.
Final Answer:
- Assertion: Incorrect
- Reason: Correct
The assertion states that if the length of the spring and the mass of the block are both halved, the angular frequency of oscillations will remain unchanged.
The reason provided states that the angular frequency (ω) is given by the formula:
ω=√km
where k is the spring constant and m is the mass of the block.
If the mass m is halved, we have:
m′=m2
The spring constant k is inversely proportional to the length of the spring. If the length L is halved, the new spring constant k′ will be:
k′=2k
(because k∝1L)
Now, substituting k′ and m′ into the angular frequency formula:
ω′=√k′m′=√2km2=√2k⋅2m=√4km=2√km=2ω
This shows that the new angular frequency ω′ is actually twice the original angular frequency ω.
Since the new angular frequency is 2ω, the assertion that the angular frequency remains unchanged is incorrect. However, the reason provided about the formula for angular frequency is correct.
- Assertion: Incorrect
- Reason: Correct
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Miscellaneous Examples
8 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Knowledge Check
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
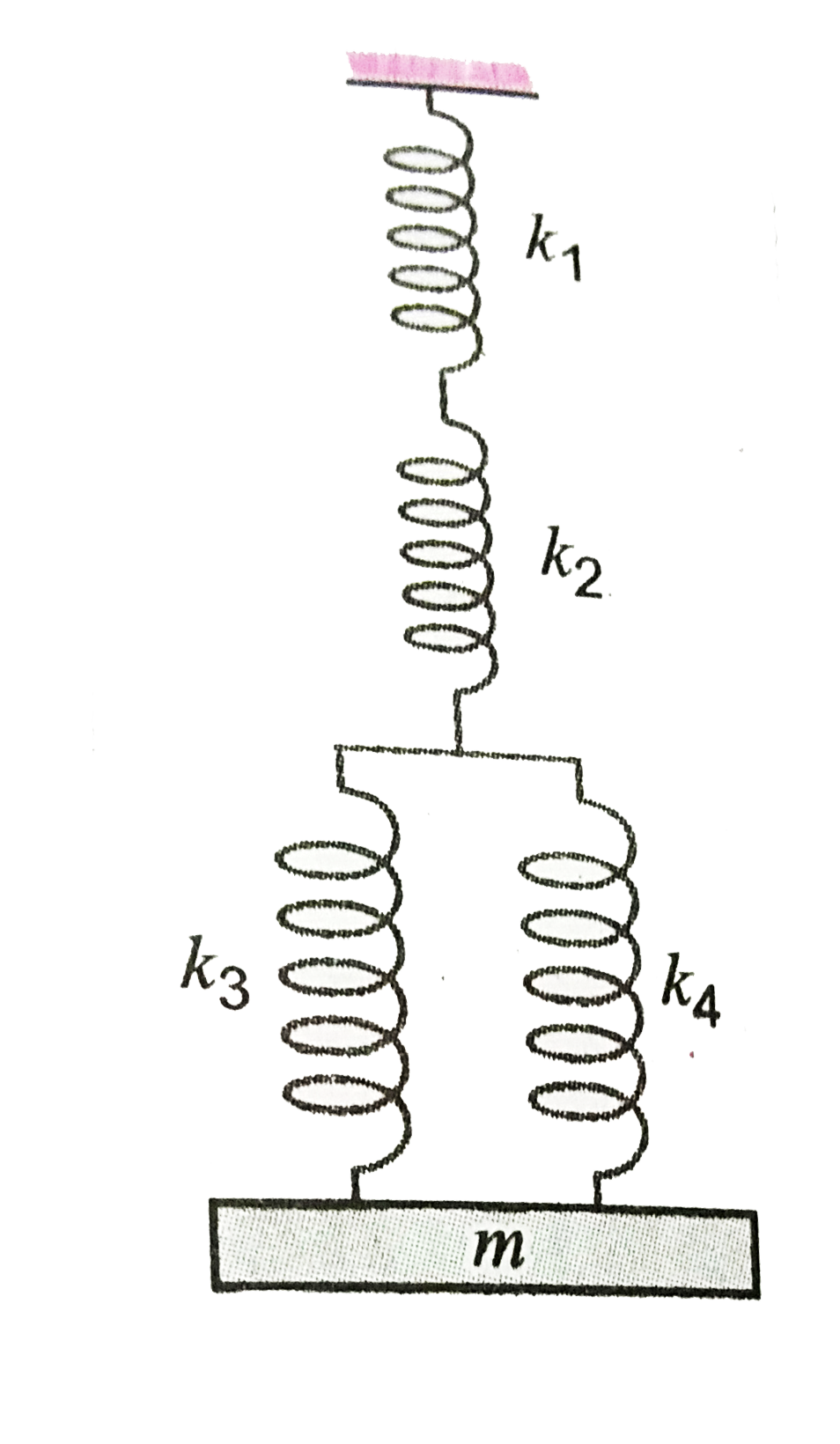 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
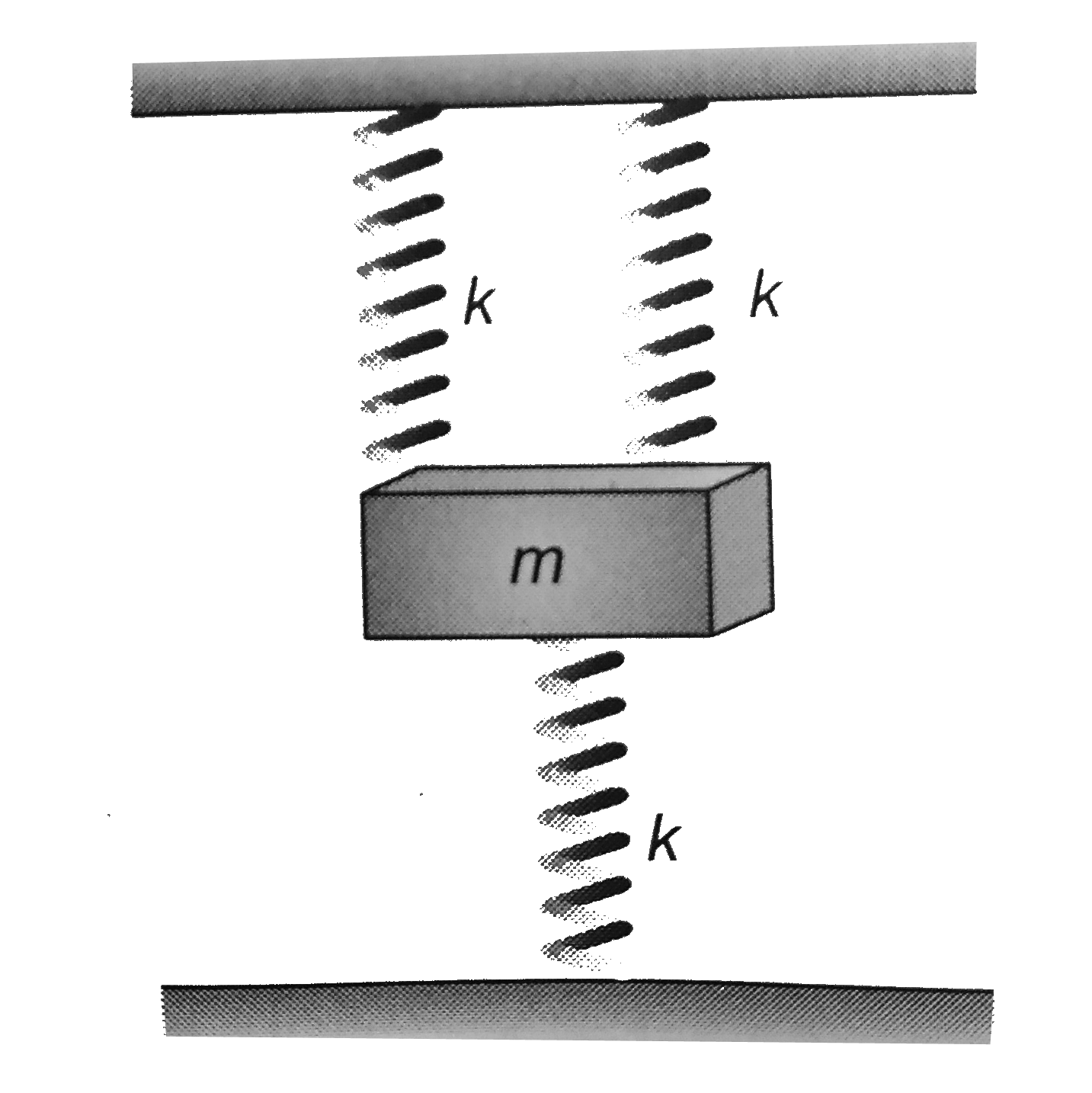
In the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
View SolutionTwo equal masses are connected by a spring satisfying Hook's law and are placed on a frictionless table. The spring is elongated a little and allowed to go. Let the angular frequency of oscillations be ω. Now one of the masses is stopped. The square of the new angular frequency is :
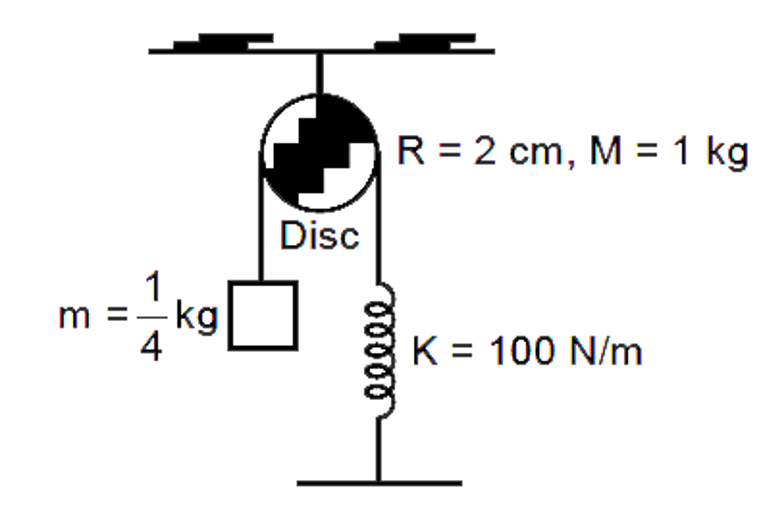
View SolutionPassage VII There is a spring block system in a lift moving upwards with acceleration a=g2
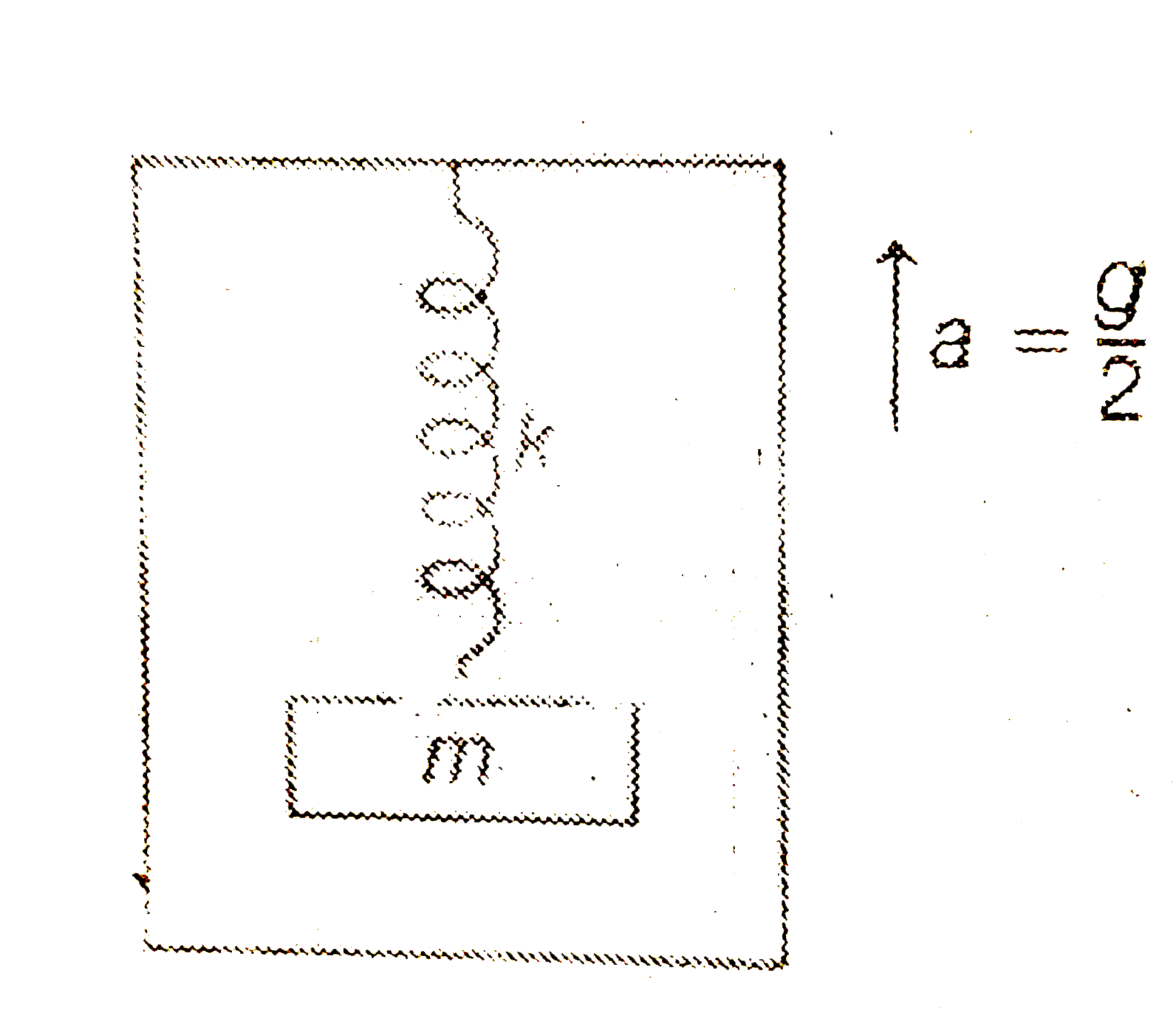
In mean position (of block's oscillations) spring is
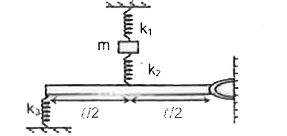
View SolutionFind the angular frequency of small oscillation of block m in the arrangement shown. Rod is massless. [Assume gravity to be absont]
View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
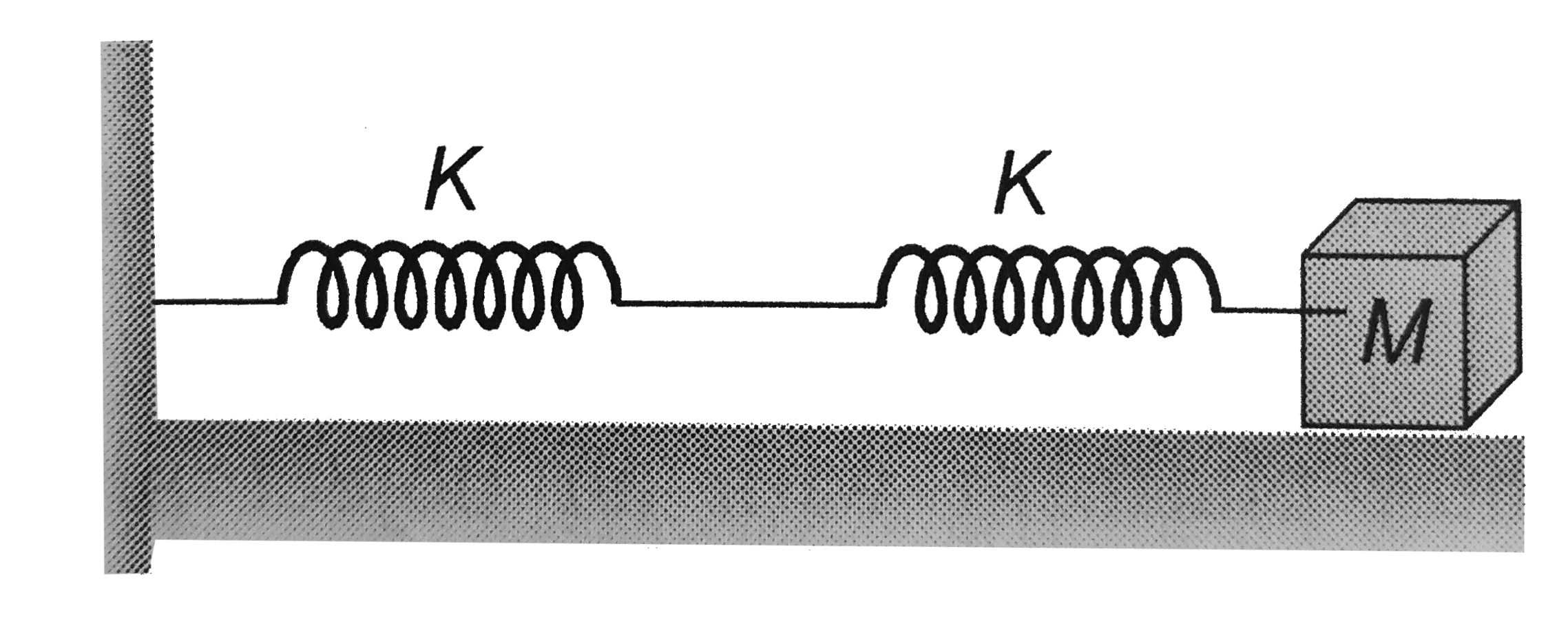
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
View SolutionA block of mass m connected with a smooth prismatic wedge of mass M is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View Solution