Assertion: In the YDSE apparatus shown in figure dltltD and dλ=4, then second order maxima will be obtained at θ=30∘
Reason: Total seven maxima will be obtained on screen.
(a)If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
(b)If both Assertion and Reason are true and the Reason is not the correct explanation of the Assertion.
(c) If Assertion is true, but the Reason is false.
(d) If Assertion is false, but the Reason is true.
The correct Answer is:B
dsinθ=2λ (for second order maxima)
sinθ=2λd=2×14=12
∴θ=30∘
For maxima, dsinθ=nλ
∴nmax=dλ=4 (fortheta =90^@)<br>So,thereare→tal7maximacorrespond∈g→<br>n=0, +-1, +-2 and +-3.<br>Weca∩ottaken=4,asitisfortheta = 90^@, which is
out of screen.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1 Objective11videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Objective question2videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Exercise 32.26videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
Similar Questions
In the YDSE apparatus shown in figure, d<<D and d=6λ. Find

(a) total number of maximas and minimas on the screen .
(b) two y-coordinates corresponding to third order maxima.View SolutionAssertion: Two coherent sources S1andS2 are placed in front of a screen as shown in figure. At point P, 10th order maxima is obtained. Then , 11th order maxima will be obtained above P.
Reason: For 11th order maxima path difference should be more.View SolutionIn the set up shown in figure dltltD and d=4lambda, find.
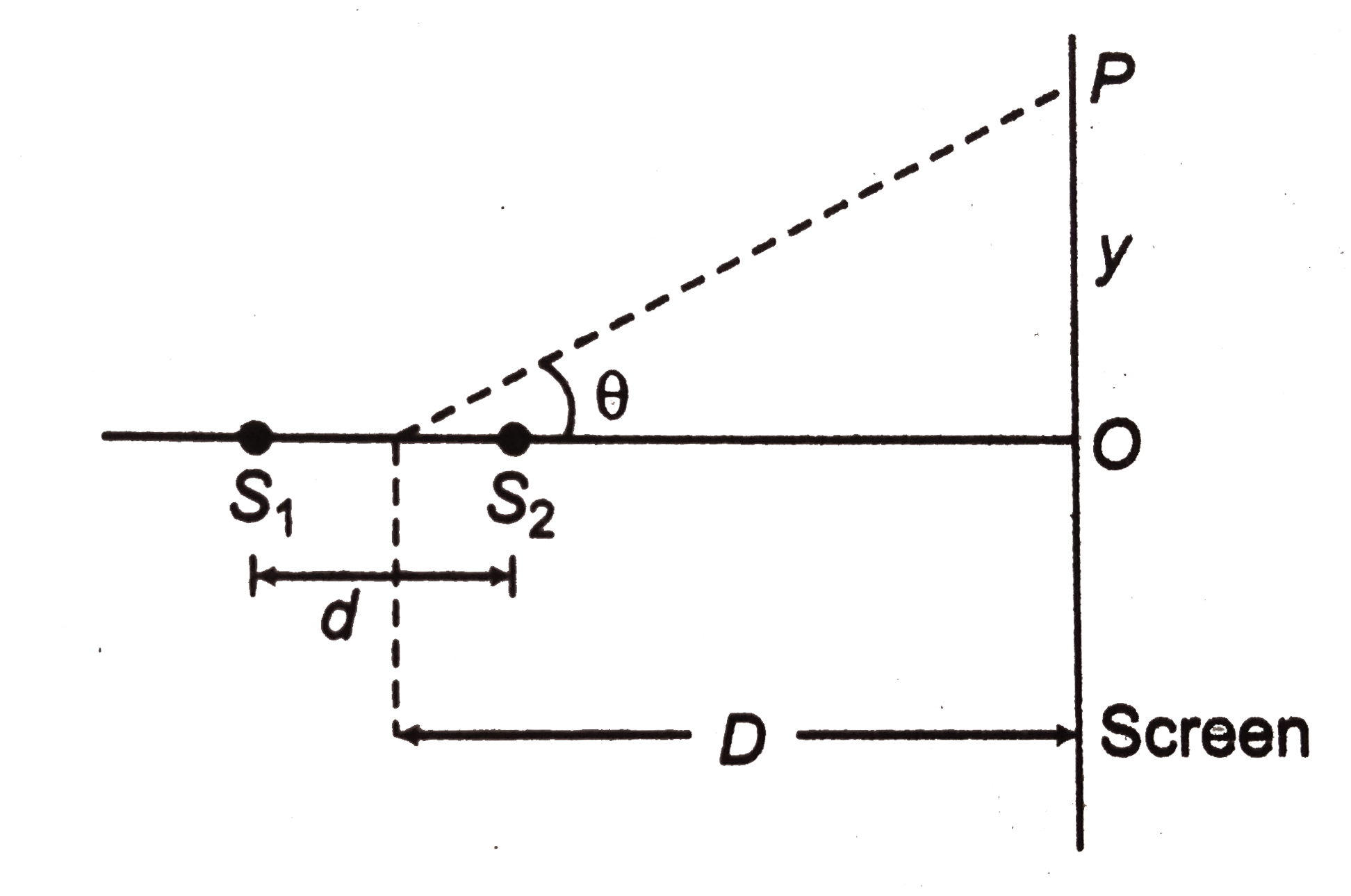
(a) total number of maximas and minimas on the screen
(b) y-coordinates corresponding to minima nearest to O.View SolutionA plane wavefront (wavelength=λ) is falling on YDSE apparatus as shown in the figure. The lower half of it is filled with water (refractive index =1.5). How many maximas can be theoretically obtained on the screen if d=98λ and D=20000λ (including the maxima at infinity)
 View Solution
View SolutionIn YDSE apparatus shown in figure wavlength of light used is λ. The screen is moved away form the source with a constant speed v. Initial distance between screen and plane of slits was D.

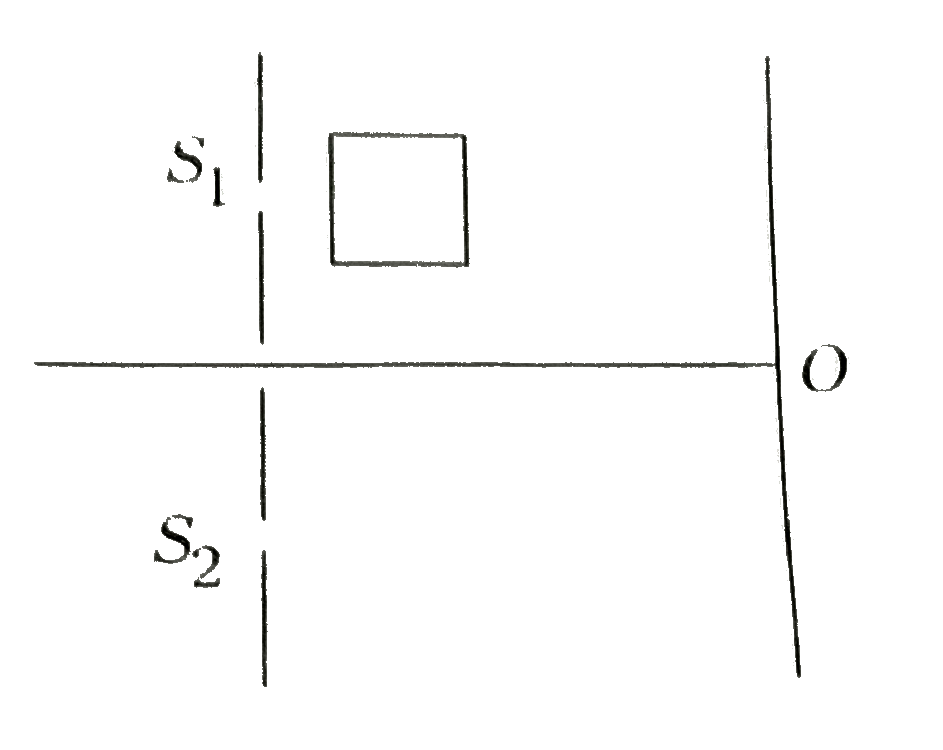
At a point P on the screen the order of fringe willView SolutionAssertion In the YDSE set up shown in figure a glass slab is inserted in front of the slit S1 as shown in figure Then zero order maxima (where path difference =0) will lie above point O.
Reason Glass slab will produce an extra path difference in the path of the ray passing through S1
 View Solution
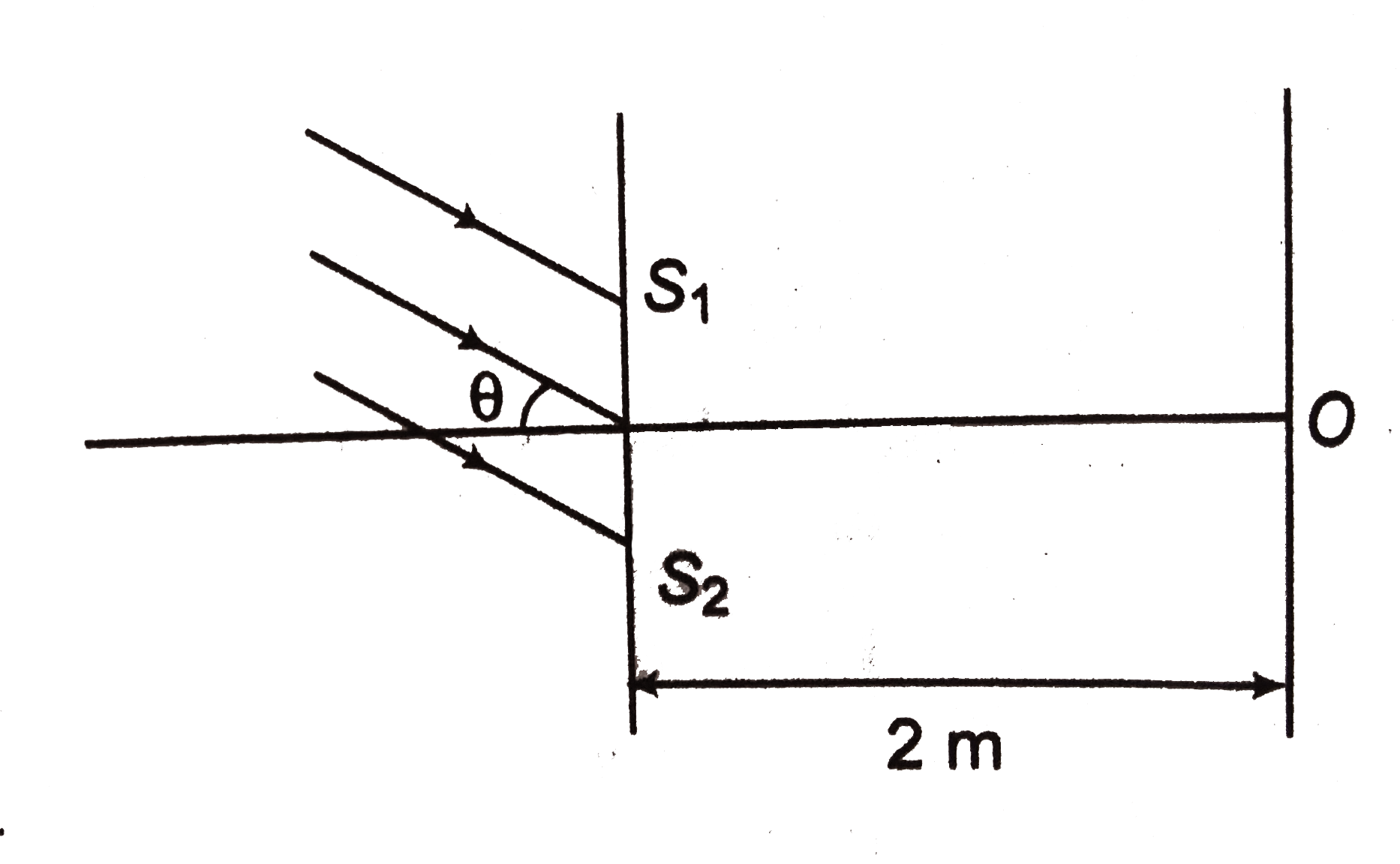
View SolutionA parallel beam of light (λ=5000Å) is incident at an angle θ=30∘ with the normal to the slit plane in a Young's double slit experiment. The intensity due to each slit is I0. Point O is equidistant from S1andS2. The distance between slits is 1mm.
 View Solution
View SolutionAssertion: In the figure shown, zero order maxima will lie above point O.
Reason: Zero order maxima normally means a point where path difference is zero.View SolutionIn YDSE, d=5λ, then the total no. of maxima observed upon screen will be
View SolutionIn a YDSE, D=1M,d=1mm,andλ=1/2mm.
(a) Find the distance between the first and central maxima on the screen.
(b) Find the number of maxima and minima obtained on the screen.View Solution
