Assertion : In x-=3+4 cosωt , amplitude of oscillation is 4 units.
Reason : Mean position is at x=3.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:B
(b) X=x−4=4cosωt⇒X=0 at x=3
Similar Questions
By means of plotting find the amplitude of the oscillation resulting from the addition of the following three oscillations of the same direction:
ξ1=acosωt,ξ2=2asinωt,ξ3=1.5acos(ωt+π/3).
View SolutionThe particle is moving such that its displacement along x-axis as a function of time is given by x(x−6)=1−10cosωt. Find amplitude, time period and mean position.
View Solution
Knowledge Check
Assertion : The amplitude of oscillation can never be infinite. lt brgt Reason : The energy of oscillator is continuously dissipated.
AIf both assertion and reason are true and the reason is the correct explanation of the assertion.BIf both assertion and reason are true but reason is not the correct explanation of the assertion.CIf assertion is true but reason is false.DIf the assertion and reason both are falseAssertion : In x=5-4sinωt , motion of body is SHM about the mean position x=5
Reason Amplitude of oscillation is 9.AIf both Assertion and Reason are correct and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.CIf Assertion is true but Reason is false.DIf Assertion is false but Reason is true.A particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is V(x)=k|x|3 where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
Aproportional to 1/√aBindependent of (a)Cproportional to √aDproportional to a3/2.
The position of S.H.M. is given by x=2[√3sinπt+cosπt]. The amplitude of motion is [ x is in metre and symbols have the usual meaning]
View SolutionUsing graphical means find an amplitude a of oscillations resulting from the superposition of the following oscillations of the same direction :
(a)x1=3.0cos(ωt+π/3),x2=8.0sin(ωt+π/6),
(b) x1=3.0cosωt,x2=5.0cos(ωt+π/4),x3=6.0sinωt.
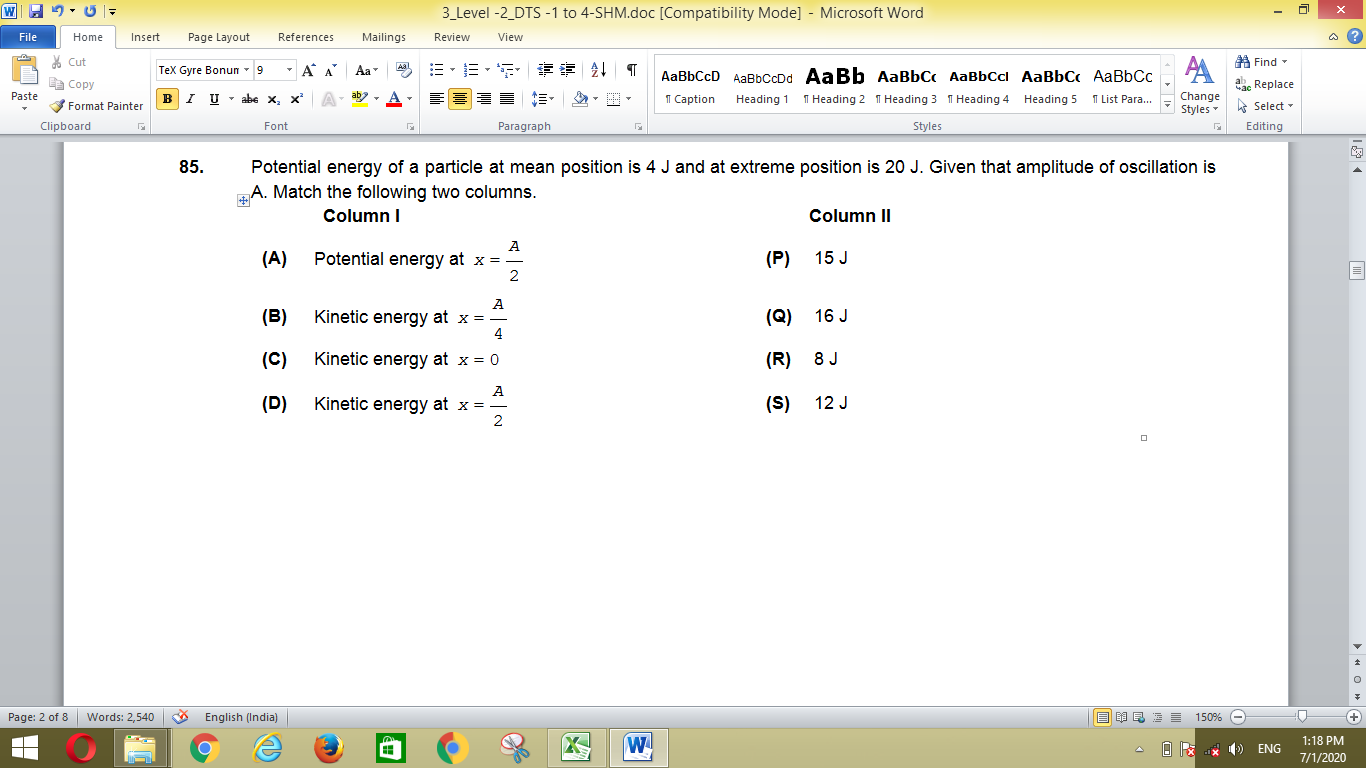
View SolutionPotential energy of a particle at mean position is 4 J and at extreme position is 20 J. Given that amplitude of oscillation is A. Match the following two columns
View SolutionAssertion : For an oscillating simple pendulum, the tension in the string is maximum at the mean position and minimum at the extreme position. lt brgt Reason : The velocity of oscillating bob in simple harmonic motion is maximum at the mean position.
View SolutionThe period of oscillation of a particle in SHM is 4sec and its amplitude of vibration is 4cm. The distance of the particle 0.5s after passsing the mean position is
View Solution
