Assertion : Particle A is moving Eastwards and particle B Northwards with same speed. Then, velocity of A with respect to B is in South-East direction.
Reason : Relative velocity between them is zero as their speeds are same.
If both Assertion and Reason are correct and Reason is the correct explanation of assertion.
If both Assertion and Reason are correct but Reason in not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:C
To solve the given question, we will analyze the assertion and reason step by step.
Step 1: Understand the Motion of Particles A and B
- Particle A is moving Eastwards, which we can represent as a vector →VA=v^i (where v is the speed and ^i is the unit vector in the East direction).
- Particle B is moving Northwards, represented as →VB=v^j (where ^j is the unit vector in the North direction).
Step 2: Calculate the Relative Velocity of A with Respect to B
- The relative velocity of A with respect to B is given by the formula:
→VA/B=→VA−→VB
- Substituting the values:
→VA/B=(v^i)−(v^j)=v^i−v^j
Step 3: Analyze the Resultant Velocity Vector
- The resultant vector →VA/B=v^i−v^j can be interpreted as having components in the East and South directions.
- To find the direction of this vector, we can visualize it in the Cartesian coordinate system:
- The positive x-direction (East) and the negative y-direction (South) indicate that the resultant vector points towards the South-East.
Step 4: Conclusion on the Assertion
- The assertion states that the velocity of A with respect to B is in the South-East direction. This is indeed correct based on our calculations.
Step 5: Analyze the Reason
- The reason states that the relative velocity between them is zero because their speeds are the same. This is incorrect because, although they have the same speed, they are moving in different directions, resulting in a non-zero relative velocity.
Final Conclusion
- The assertion is true, while the reason is false. Therefore, the correct answer is that the assertion is true, but the reason is false.
- Particle A is moving Eastwards, which we can represent as a vector →VA=v^i (where v is the speed and ^i is the unit vector in the East direction).
- Particle B is moving Northwards, represented as →VB=v^j (where ^j is the unit vector in the North direction).
- The relative velocity of A with respect to B is given by the formula:
→VA/B=→VA−→VB
- Substituting the values:
→VA/B=(v^i)−(v^j)=v^i−v^j
- The resultant vector →VA/B=v^i−v^j can be interpreted as having components in the East and South directions.
- To find the direction of this vector, we can visualize it in the Cartesian coordinate system:
- The positive x-direction (East) and the negative y-direction (South) indicate that the resultant vector points towards the South-East.
- The assertion states that the velocity of A with respect to B is in the South-East direction. This is indeed correct based on our calculations.
- The reason states that the relative velocity between them is zero because their speeds are the same. This is incorrect because, although they have the same speed, they are moving in different directions, resulting in a non-zero relative velocity.
- The assertion is true, while the reason is false. Therefore, the correct answer is that the assertion is true, but the reason is false.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Mathch the columns)
6 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (A) Taking it together
75 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
Four particles A, B, C and D are moving with constant speed v each. At the instant shown relative velocity of A with respect to B, C and D are in directions :-
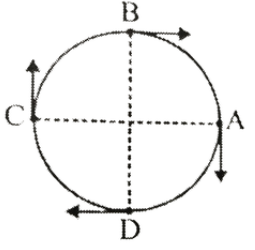
View SolutionFour particles A, B, C and D are moving with constant speed v each at the instant shown relative velocity of A with respect to B, C and D are in directions
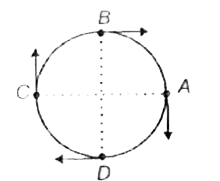
View Solution
Knowledge Check
A particle is moving on a circular path with a constant speed v. Its change of velocity as it moves from A to B is:
 A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
Two particles A and B moving in a plane have velocities as shown in figure .Relative velocity of A w.r.t B
View SolutionConsider a collection of a large number of particles each with speed v. The direction of velocity is randomly distributed in the collection. Show that the magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection is greater than v.
View Solution
Mirror is moving towards the particle with speed 2 cm/sec. Speed of A ad B are 10√2 and 5 cm/sec respectively in the direction shown in figure. Magnitude of velocity of image of the particle B with respect to image of A.
View SolutionA particle is moving eastwards with velocity of 5m/s. In 10sec the velocity changes to 5m/s northwards. The average acceleration in this time is.
View SolutionA particle is moving eastwards with a velocity of 5ms−1. In 10seconds the velocity changes to 5ms−1 northwards. The average acceleration in this time is
View SolutionParticles AandB move with constant and equal speeds in a circle as shown in (Fig. 5.164). Find the angular velocity of the particle A with respect to B, if the angular velocity of particle Aw.r.t.O is ω.
 .
.
View SolutionGive examples for the particle where (a) the velocity is in opposite direction to the acceleration (b)the velocity of the particle is zero but is acceleration is not zero.
View Solution
