Consider a collection of a large number of particles each with speed v. The direction of velocity is randomly distributed in the collection. Show that the magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection is greater than v.
zero
greater thanv
less than v
v
The correct Answer is:B
To solve the problem, we need to find the average magnitude of the relative velocity between pairs of particles in a collection where each particle has the same speed v but with randomly distributed directions. Let's go through the steps systematically.
Step 1: Define the Relative Velocity
Let →VA and →VB be the velocity vectors of two particles A and B, respectively. Since both particles have the same speed v, we can express their velocities as:
|→VA|=|→VB|=v
The relative velocity →VAB of particle A with respect to particle B is given by:
→VAB=→VA−→VB
Step 2: Calculate the Magnitude of the Relative Velocity
The magnitude of the relative velocity can be expressed as:
|→VAB|=|→VA−→VB|
Using the formula for the magnitude of the difference of two vectors, we have:
|→VAB|=√|→VA|2+|→VB|2−2|→VA||→VB|cosθ
where θ is the angle between the two velocity vectors →VA and →VB.
Step 3: Substitute the Magnitudes
Substituting |→VA|=v and |→VB|=v:
|→VAB|=√v2+v2−2v2cosθ=√2v2(1−cosθ)=v√2(1−cosθ)
Using the identity 1−cosθ=2sin2(θ/2):
|→VAB|=v√2⋅2sin2(θ/2)=2vsin(θ/2)
Step 4: Average the Magnitude of Relative Velocity
To find the average magnitude of the relative velocity over all pairs of particles, we need to integrate over all possible angles θ from 0 to 2π:
⟨|→VAB|⟩=12π∫2π02vsin(θ2)dθ
This simplifies to:
⟨|→VAB|⟩=vπ∫2π0sin(θ2)dθ
Step 5: Solve the Integral
To solve the integral, we can use the substitution u=θ2, which gives dθ=2du:
∫2π0sin(θ2)dθ=2∫π0sin(u)du=2(−cos(u))π0=2((−cos(π))−(−cos(0)))=2(1+1)=4
Thus, we have:
⟨|→VAB|⟩=vπ⋅4=4vπ
Step 6: Conclusion
Since 4π is greater than 1 (approximately 1.273), we conclude that:
⟨|→VAB|⟩>v
This shows that the average magnitude of the relative velocity between pairs of particles is indeed greater than v.
Let →VA and →VB be the velocity vectors of two particles A and B, respectively. Since both particles have the same speed v, we can express their velocities as:
|→VA|=|→VB|=v
The relative velocity →VAB of particle A with respect to particle B is given by:
→VAB=→VA−→VB
The magnitude of the relative velocity can be expressed as:
|→VAB|=|→VA−→VB|
Using the formula for the magnitude of the difference of two vectors, we have:
|→VAB|=√|→VA|2+|→VB|2−2|→VA||→VB|cosθ
where θ is the angle between the two velocity vectors →VA and →VB.
Substituting |→VA|=v and |→VB|=v:
|→VAB|=√v2+v2−2v2cosθ=√2v2(1−cosθ)=v√2(1−cosθ)
Using the identity 1−cosθ=2sin2(θ/2):
|→VAB|=v√2⋅2sin2(θ/2)=2vsin(θ/2)
To find the average magnitude of the relative velocity over all pairs of particles, we need to integrate over all possible angles θ from 0 to 2π:
⟨|→VAB|⟩=12π∫2π02vsin(θ2)dθ
This simplifies to:
⟨|→VAB|⟩=vπ∫2π0sin(θ2)dθ
To solve the integral, we can use the substitution u=θ2, which gives dθ=2du:
∫2π0sin(θ2)dθ=2∫π0sin(u)du=2(−cos(u))π0=2((−cos(π))−(−cos(0)))=2(1+1)=4
Thus, we have:
⟨|→VAB|⟩=vπ⋅4=4vπ
Since 4π is greater than 1 (approximately 1.273), we conclude that:
⟨|→VAB|⟩>v
This shows that the average magnitude of the relative velocity between pairs of particles is indeed greater than v.
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
A large number of particles are moving each with speed v having directions of motion randomly distributed. What is the average relative velocity between any two particles averaged over all the pairs?
View SolutionUnder what condition is the magnitude of the average velocity of a particle moving in onbe dimension smaller than the average speed over same time interval?
View SolutionA particle is projected with a speed v and an angle θ to the horizontal. After a time t, the magnitude of the instantaneous velocity is equal to the magnitude of the average velocity from 0 to t. Find t.
View SolutionIn a collinear collision, a particle with an initial speed v0 strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is :
View SolutionA particle moves with constant speed v along a regular hexagon ABCDEF in the same order. Then the magnitude of the avergae velocity for its motion form A to
View SolutionThe fig. shows the displacement time graph of a particle moving on a straight line path. What is the magnitude of average velocity of the particle over 10 seconds?
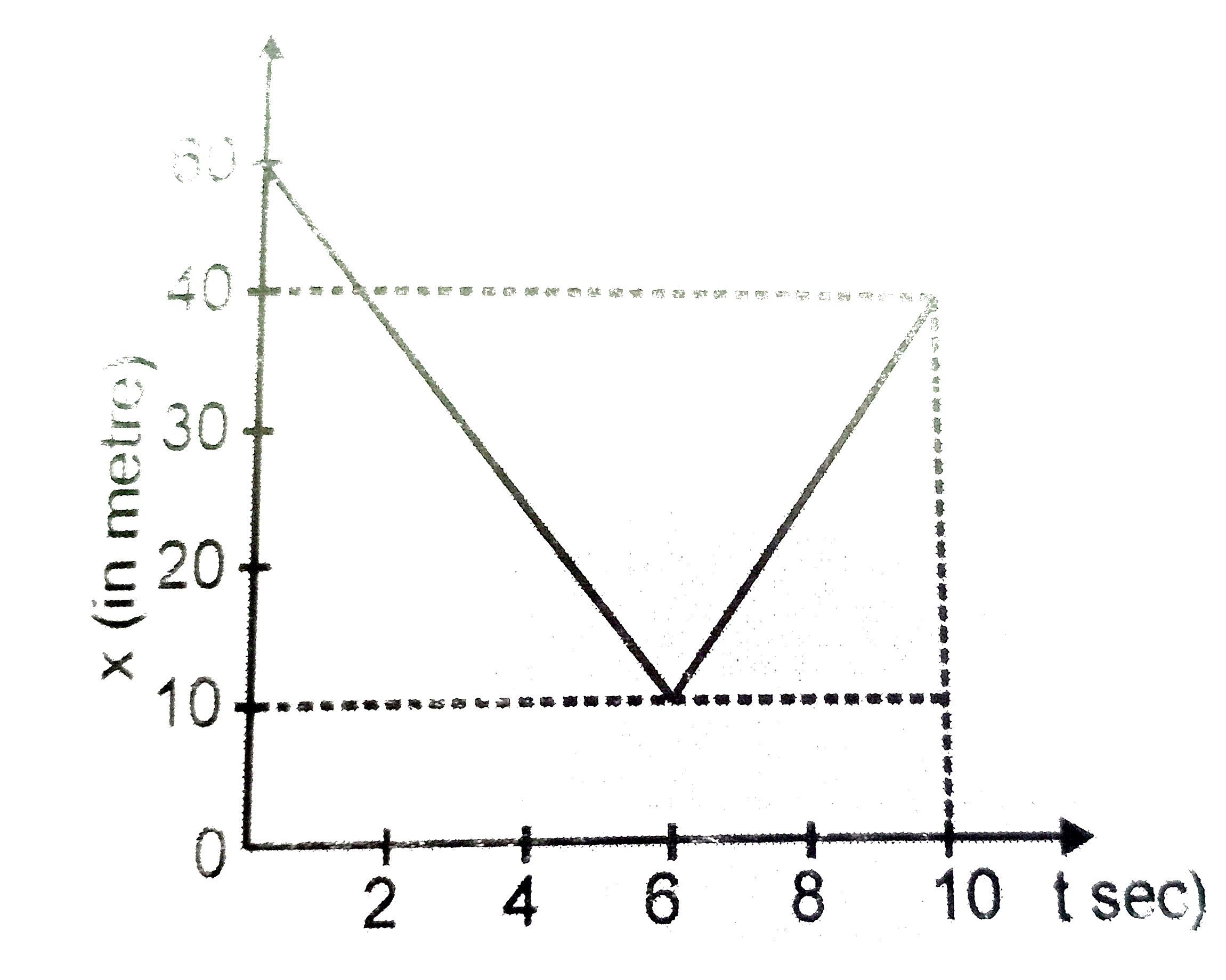
View SolutionAssertion : Particle A is moving Eastwards and particle B Northwards with same speed. Then, velocity of A with respect to B is in South-East direction.
Reason : Relative velocity between them is zero as their speeds are same.
View SolutionThe velocity of a particle moving in the positive direction of the x axis varies as v=α√x, where α is a positive constant. Assuming that at the moment t=0 the particle was located at the point x=0, find:
(a) the time dependence of the velocity and the acceleration of the particle,
(b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.
View SolutionThe velocity of particle moving in the positive direction of x axis varies as v=α√x, where α is a positive constnat. Assuming that at moment t=0, the particle was located at the point x=0. find.
(a) the time dependence of the velocity and the acceleration of the particle.
(b) the mean velocity of the particle averaged over the time that the particle takes to cover first s meters of the path
View SolutionTwo cars are moving is one a same line dimension in opposite direction with the same speed v. The relative velocity of two cars w.r.t. each other is
View Solution
