Assertion : The power in ac circuit is minimum if the circuit has only a resistor.
Reason : Power of a circuit is independent of the phase angle.
If both assertion ans reason are true ans reaason is the correct explanation of assertion.
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion istrue but reason is false.
If both assertion and reason are false.
The correct Answer is:D
To solve the question, we need to analyze both the assertion and the reason provided.
Step 1: Analyze the Assertion
The assertion states that "The power in an AC circuit is minimum if the circuit has only a resistor."
- In an AC circuit, the power (P) is given by the formula:
P=Vrms×Irms×cosϕ
where ϕ is the phase angle between the voltage and current.
- For a purely resistive circuit, the phase angle ϕ is 0 degrees (or 0 radians), which means cosϕ=1. Therefore, the power is maximum, not minimum.
Conclusion for Assertion:
The assertion is false because the power is maximum in a purely resistive circuit, not minimum.
Step 2: Analyze the Reason
The reason states that "Power of a circuit is independent of the phase angle."
- From the power formula, we see that power is indeed dependent on the phase angle ϕ since it directly affects the value of cosϕ.
- When ϕ=90∘ (or π/2 radians), cosϕ=0, resulting in zero power. This shows that power is very much dependent on the phase angle.
Conclusion for Reason:
The reason is false because the power in an AC circuit is dependent on the phase angle.
Final Conclusion:
Since the assertion is false and the reason is also false, the correct answer is that both the assertion and the reason are incorrect.
Summary of the Answer:
- Assertion: False
- Reason: False
- Therefore, the correct option is that both the assertion and reason are false.
---
The assertion states that "The power in an AC circuit is minimum if the circuit has only a resistor."
P=Vrms×Irms×cosϕ
where ϕ is the phase angle between the voltage and current.
The assertion is false because the power is maximum in a purely resistive circuit, not minimum.
The reason states that "Power of a circuit is independent of the phase angle."
The reason is false because the power in an AC circuit is dependent on the phase angle.
Since the assertion is false and the reason is also false, the correct answer is that both the assertion and the reason are incorrect.
- Assertion: False
- Reason: False
- Therefore, the correct option is that both the assertion and reason are false.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Ac Voltage Applied To A Resistor
17 Videos
- ALTERNATING CURRENT BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Ac Voltage Applied To A Inductor
5 Videos
- ALTERNATING CURRENT BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - NCERT
7 Videos
- ATOMS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ATOMS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
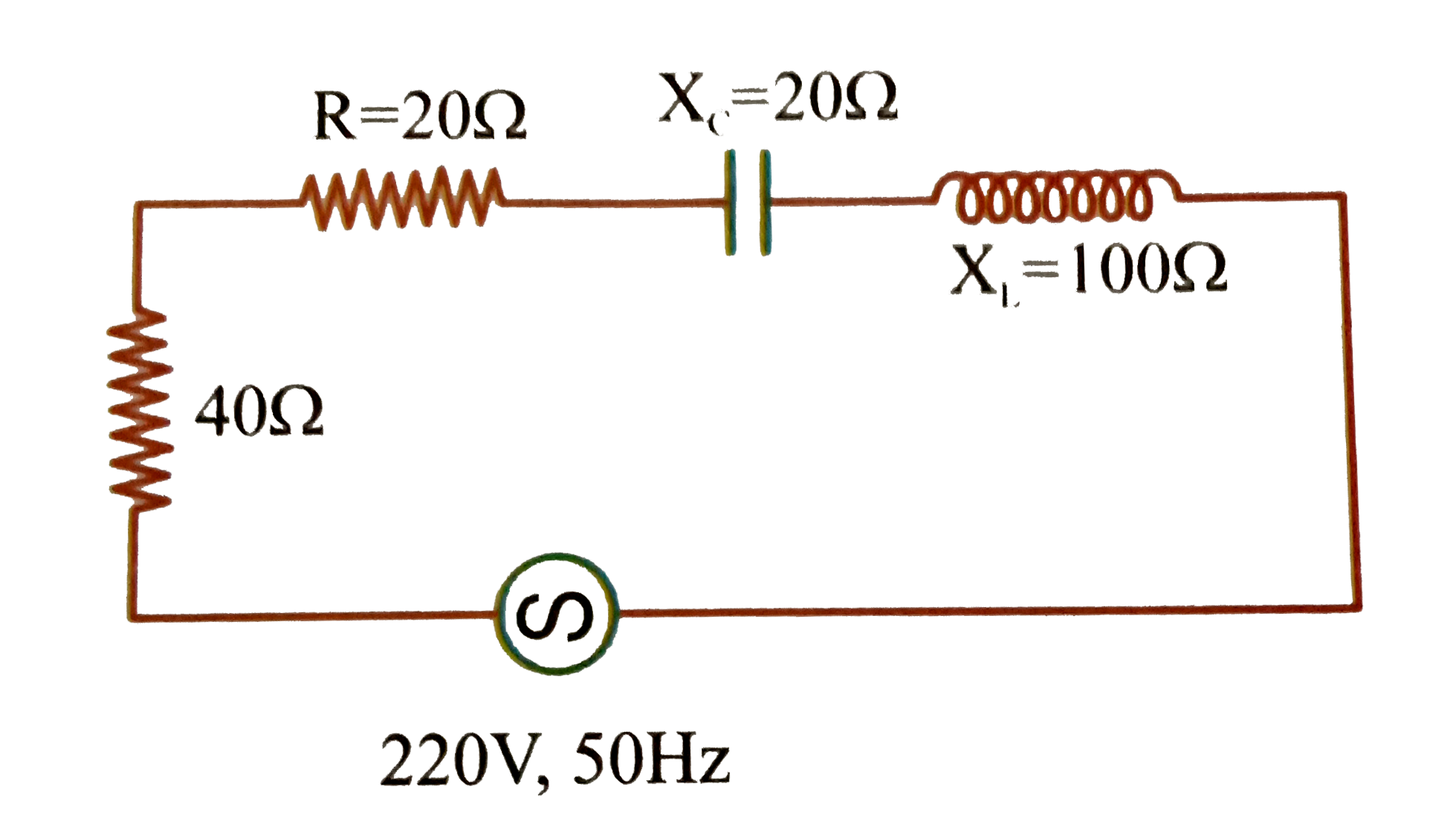
The power factor of the circuit as shown in figure is
 A0.2B0.4C0.8D0.6
A0.2B0.4C0.8D0.6
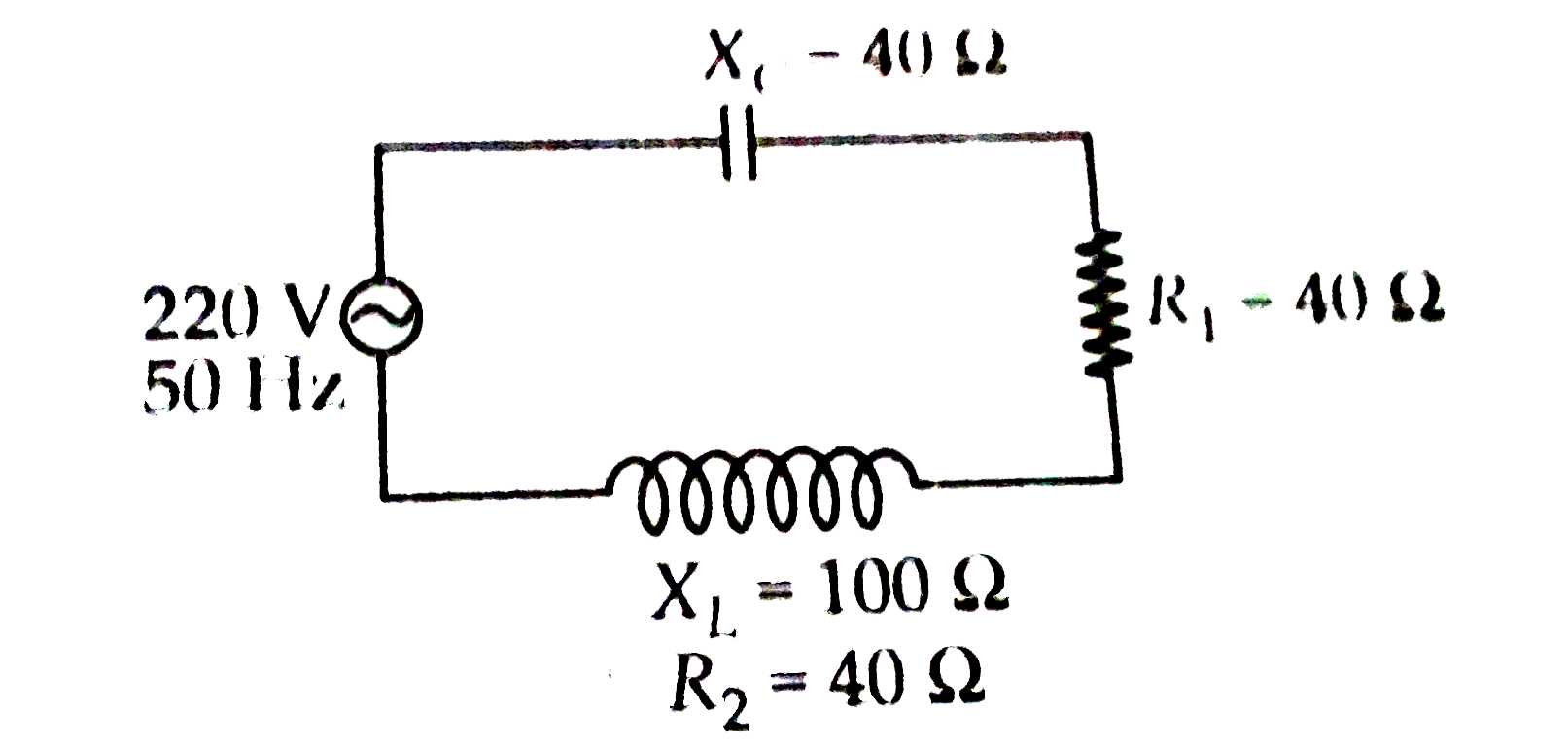
The total power dissipated in watts in the circuit shown here is
View SolutionPower factor of the circuit shown here is

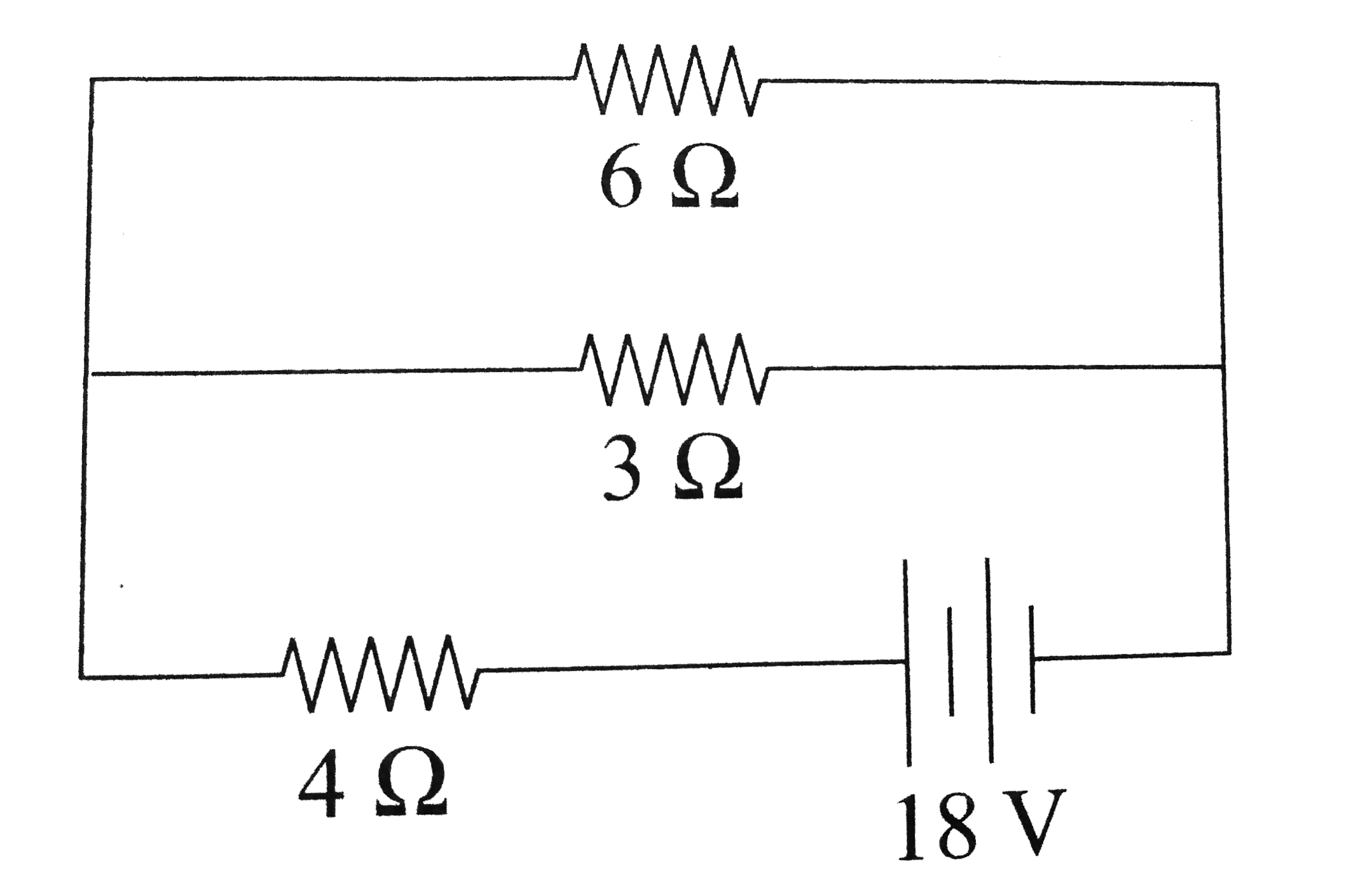
View SolutionAssertion: In the part of the circuit shown in figure, maximum power is produced across R.
Reason : Power P=V2R
View SolutionThe power dissipated in the adjacent circuit is -
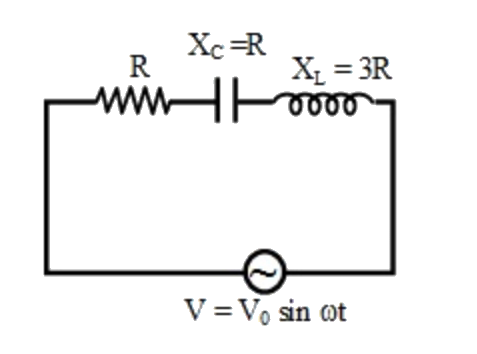
View SolutionIf the power dissipated in the circuit is 4W then the value of R is:
_2019_CBT7_E01_014_Q01.png)
View SolutionIf the power dissipated in the circuit is 4W then the value of R is:
_2019_CBT7_E01_014_Q01.png)
View SolutionThe power consumption by the circuit shown in figure at steady state is
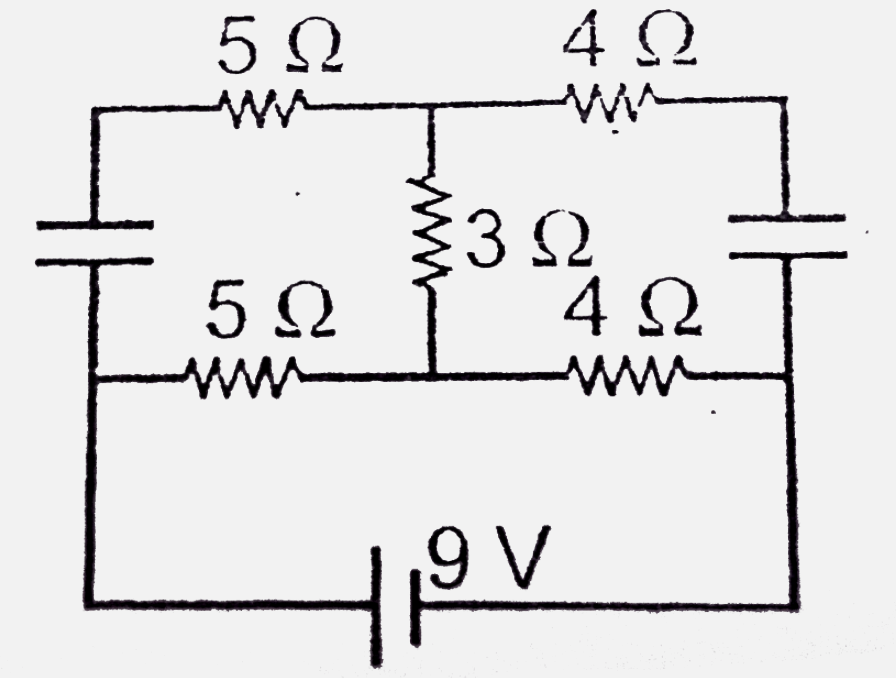
View Solution