Assertion: There is a triangular plate as shown. A dotted axis is lying in the plane of slab. As the axis is moved downwards, moment of inertia of slab will first decrease then increase.
Reason: Axis is first moving towards its centre of mass and then it is receding from it.
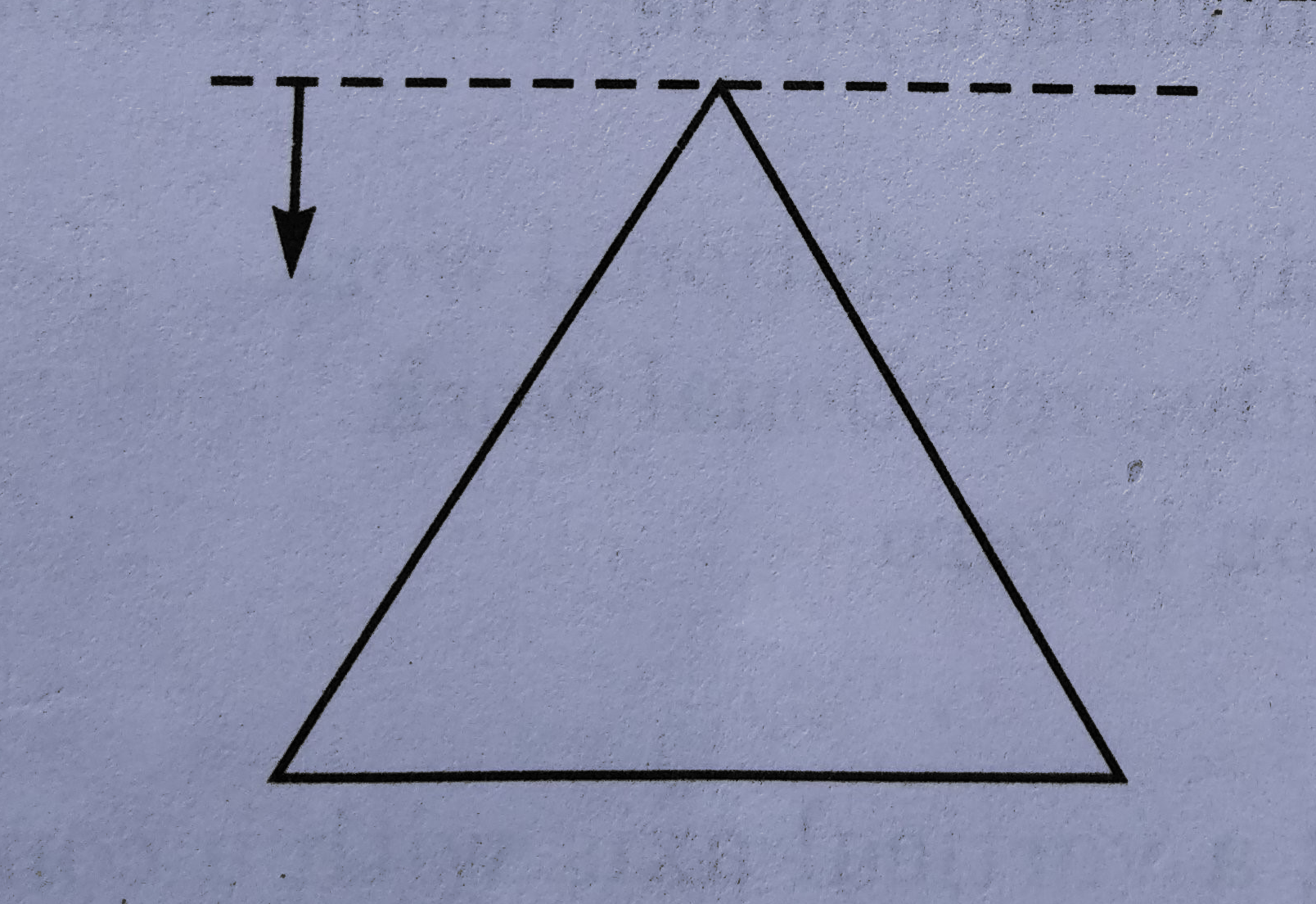
Both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
Both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
Assertion is true, but the reaction is false.
Assertion is false but the reason is true.
Step by step video & image solution for Assertion: There is a triangular plate as shown. A dotted axis is lying in the plane of slab. As the axis is moved downwards, moment of inertia of slab will first decrease then increase. Reason: Axis is first moving towards its centre of mass and then it is receding from it. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.11
2 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Assertion : Two axes AB and CD are as shown in figure. Given figure is of a semi-circular ring. As the axis moves from AB towards CD, moment of inertia first decreases, then increases.

Reason : Centre of mass lies somewhere between AB and CD.
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View Solution
Assertion: There is a thin rod AB and a dotted line CD. All the axes we are talking about are perpendicular to plane . As we take different axes moving from A to D, moment of inertia of the rod may first decrease then increase.
Reason: Theorem of perpendicular axis cannot be applied here.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionIn the figure shown find the moment of inertia of square plate having mass m and sides a. About an axis 2 passing through point C (centre of mass) and in the plane of plate?

View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of a solid cylinder of density ρ, radius of base r, and height h about an axis passing through its centre of mass and parallel to length is
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is

View Solution