Assume a planet is a uniform sphere of radius R that (somehow) has a narrow radial tunnel through its center (Fig. 13-8). Also assume we can position an apple anywhere along the tunnel or outside the sphere. Let FR be the magnitude of the gravitational force on the apple when it is located at the planet's surface. How far from the surface is there a point where the magnitude is 1/3FR if we move the apple (a) away from the planet and (b) into the tunnel?
(a) r=R√3, (b) r = R/3
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)16videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)7videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - CHECKPOINT5videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)4videos
GEOMETRICAL OPTICS : REFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)5videos
HEAT-MEASUREMENT AND TRANSFER
Similar Questions
An apple falls from a tree because of gravitational between the earth and apple. If F1 is the magnitude of force exerted by the earth on the apple and F2 is the magnitude of force exerted by apple on earth, then
View SolutionThe magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
View Solution
Knowledge Check
- Question 1 - Select One
An apple falls from a tree because of gravitational between the earth and apple. If F1 is the magnitude of force exerted by the earth on the apple and F2 is the magnitude of force exerted by apple on earth, then
AF1 is very much greater than F2BF2 is very much greater than F1CF1 is only a little greater than F2DF1 and F2 are equal - Question 2 - Select One
Flux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
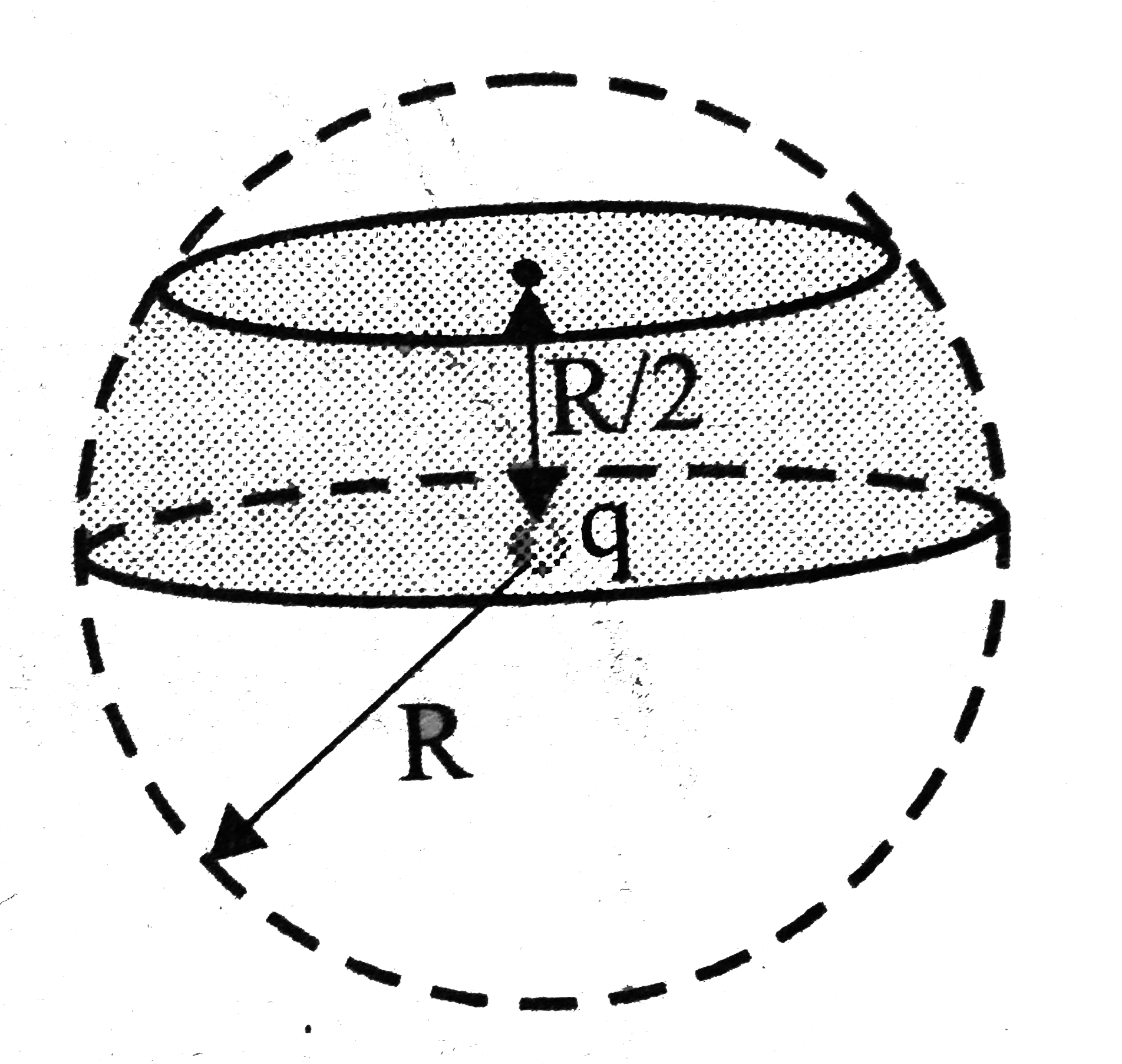 Aqε0Bq2ε0Cq4ε0Dzero
Aqε0Bq2ε0Cq4ε0Dzero
If the force of gravitation acts on apples on the tree at different height from the surface of the earth, can it act on even farther objects like the other planets and the sun ?
View SolutionThe ratio of acceleration due to gravity at depth 'R' from the surface of planet and at height ' r' from the surface of planet where r
View SolutionThe work done by gravitational force on a point mass m0in moving from the surface of a planet off mass M and radius R to a height R2 is
View SolutionThe work done by gravitational force on a point mass m0in moving from the surface of a planet off mass M and radius R to a height R2 is
View SolutionA uniform solid sphere of radius R produces a gravitational acceleration of ag on its surface. At what distance from the sphere's center are there points (a) inside and (b) outside the sphere where the gravitational acceleration is ag/2?
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
 View Solution
View Solution

