An apple falls from a tree because of gravitational between the earth and apple. If F1 is the magnitude of force exerted by the earth on the apple and F2 is the magnitude of force exerted by apple on earth, then
F1 is very much greater than F2
F2 is very much greater than F1
F1 is only a little greater than F2
F1 and F2 are equal
The correct Answer is:D
To solve the problem, we will analyze the forces acting between the Earth and the apple based on Newton's law of gravitation.
1. Understanding the Forces:
- When an apple falls from a tree, it experiences a gravitational force due to the Earth. This force can be denoted as F1, which is the force exerted by the Earth on the apple.
- Simultaneously, the apple also exerts a gravitational force on the Earth, which we denote as F2.
2. Applying Newton's Third Law of Motion:
- According to Newton's Third Law of Motion, for every action, there is an equal and opposite reaction. This means that the force exerted by the Earth on the apple (F1) is equal in magnitude and opposite in direction to the force exerted by the apple on the Earth (F2).
- Mathematically, this can be expressed as:
F1=F2
3. Conclusion:
- Since both forces are equal in magnitude, we conclude that:
F1 (force by Earth on apple)=F2 (force by apple on Earth)
- Therefore, the correct answer to the question is that F1 and F2 are equal.
Final Answer:
- F1 and F2 are equal.
- When an apple falls from a tree, it experiences a gravitational force due to the Earth. This force can be denoted as F1, which is the force exerted by the Earth on the apple.
- Simultaneously, the apple also exerts a gravitational force on the Earth, which we denote as F2.
- According to Newton's Third Law of Motion, for every action, there is an equal and opposite reaction. This means that the force exerted by the Earth on the apple (F1) is equal in magnitude and opposite in direction to the force exerted by the apple on the Earth (F2).
- Mathematically, this can be expressed as:
F1=F2
- Since both forces are equal in magnitude, we conclude that:
F1 (force by Earth on apple)=F2 (force by apple on Earth)
- Therefore, the correct answer to the question is that F1 and F2 are equal.
- F1 and F2 are equal.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - GRAVITATIONEXERCISE - SHORT ANSWER TYPE QUESTIONS7videos
GRAVITATION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - GRAVITATIONEXERCISE - LONG ANSWER TYPE QUESTIONS4videos
GRAVITATION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - FORCE AND LAW OF MOTIONEXERCISE - LONG ANSWER3videos
FORCE AND LAW OF MOTION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOTIONEXERCISE - Long Answer Type Questions6videos
MOTION
Similar Questions
Let F1 be the magnitude of the gravitational force exerted on the Sun by Earth and F2 be the magnitude of the force exerted on Earth by the Sun. Then:
View SolutionIn the above question, find out the magnitude of net force exerted by the pulley on the rod R1:
View SolutionA book whose mass is 2 kg rests on a table. Find the magnitude of the force exerted by the table on the book.
View SolutionIf magnitude of the gravitational force between the earth and the moon is denoted by A and between the earth and the sun by B then
View SolutionIn the following figure, if magnitude of forces between B and C is F, then magnitude of force between A and B is
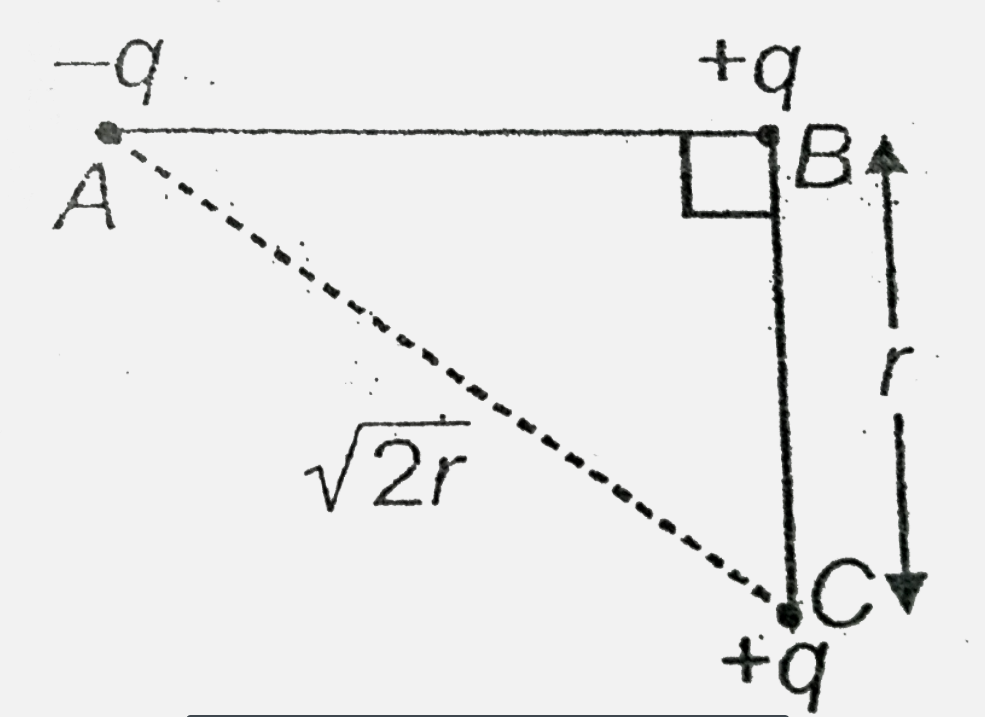 View Solution
View SolutionWeight of a person on the Earth depends on the gravitational force exerted by the Earth.
View SolutionName the following.
Gravitational force exerted by the Earth on an object .View SolutionWrite the formula to find the magnitude of the gravitational force between the Earth and an object on the surface of the Earth.
View SolutionWhen an apple falls from a tree what happens to its gravitational potential energy just as it reaches the ground? After it strikes the ground?
View SolutionThree infinetely long wires 1 , 2 and 3 carry equal currents in the directions shown in fiugre. They are placed on the vertices of an equilateral triangle. Let F be the magnitude of force between any two wires.

F1 is the magnitude of force on wire 1 and F2 the magnitude of force on wire 2. ThenView Solution

