Assume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of √(gR) (b) it is relased from a height R above the tunnel (c ) it is thrown vertically upward along the length of tunnel with a speed of √gR.
The correct Answer is:A, B, C
Let M be the total mass of the earth. At any position x.
∴M1M=p×43πx3p×43πr3×x3R3
⇒M1=Mx3R3
So, force on the particle is given by
∴Fx=GMmx2
=GMmR3x.....(1)
So, acceleration of the mass 'M' at that position is given by,
ax=GMmR3
⇒axx=ω2
=GMR3=gR(g=GMR2)
So, T=2π√Rg
= time period of ocillation
(a) Now using velocity
= displacement equation
υ=ω√(A2−Y2)
[where, A = amplitude]
Given when,
y=R,υ=√gR,w=√gR
⇒√gR=√(gR)(A2−R2)
⇒R2=A2−R2
[ Now, the phases of the particle at the point
P is grater then π2 has less then π and at
Q is grater then π but less then 3π2 Let the times taken by the particle to reach the position P and Q be t1andt2 respectively, then using displacement equation].
y = r sin omega t<br>Wehave<br>R = sqrt2 R sin omega t<br>rArr omegat_1 = (3pi)/(4)<br>Wehave,R = sqrt2 R sin omega t_1<br>rArr omega t_2 = (5pi)/(4)<br>So, omega (t_2 - t_1) = (pi)/(2)<br>rArr t_2 - t_1 = (pi)/(2omega) = ((pi)/(2))/((R )/(g))<br>Timetakenbythepartic≤→travelomP→Qis<br>t_2 - t_1 = (pi)/(2) ((R )/(g))sec.<br>(b)Whenthebodyisdroppedomaheightr,thenapply∈gconservationofe≠rgy,chan≥∈P.E.=ga∈∈K.E.<br>rArr (GMm)/(R ) - (GMm).(2R) = (1)/(2) m upsilon^2<br>rArr upsilon = sqrt(gR)<br>SincethevelocityissameatP,as∈part(a)thebodywilltakensametime→travelPQ.<br>(c)WhenthebodyisprojectedverticallyupwardomPwithavelocity.(sqrt(gR)itsvelocitywillbezeroatthehighestp∮.Thevelocityofthebody,whenreachesP,aga∈wilbe<br>upsilon = sqrt((gR))
Hece the body will take same time
π2√Rg to travel P.Q.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
Assume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to reach centre of earth if it is projected into the tunnel from surface of earth with speed needed for it to escape the gravitational field to earth.
View SolutionA ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
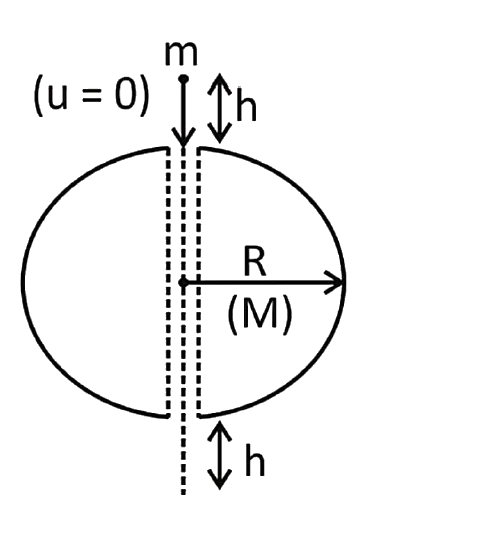
View Solution
Knowledge Check
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance (R/2) from the earth's centre, where 'R' is the radius of the Earth. The wall of the tunnel is frictionless. If a particle is released in this tunnel, it will execute a simple harmonic motion with a time period :
A2πRgBg2πrC12π√grD2π√Rg
A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionAssume that a tunnel is dug along a cord of earth at a perpendicular distance R2 from earth's centre where R is the radius of earth. The wall of tunnel is frictionless. Find the time period of particle excuting SHM in tunnel
View SolutionAssume that a tunnel ils dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. a. Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel. b. Find the component of this fore along the tunnel and perpendicular to the tunnel. c. Find the normal force exerted by the wall on the particle. d. Find the resultant force on the particle. e.Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
View SolutionAssume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless.
(a) Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel.
(b) Find the component of this force along the tunnel and perpendicular to the tunnel.
(c) Find the normal force exerted by the wall on the particle.
(d) Find the resultant force on the particles.
(e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
View SolutionAssume that a frictionless tunnel is made in the earth along its diameter, a particle in projected in the tunnel from the surface of the earth with an initial speed v0=√gR, where g is the acceleration due to gravity on the earth's surface & R is the radius of the earth, if time taken by the particle to reach the centre of the earth is πn√4Rg the value of n is?
View SolutionImagine a smooth tunnel along a chord of nonrotating earth at a distance R2 from the centre. R is the radius of the earth. A projectile is fired along the tunnel from the centre of the tunnel at a speed V∘=√gR [g is acceleration due to gravity at the surface of the earth]. (a) Is the angular momentum [about the centre of the earth] of the projectile onserved as it moves along the tunnel? (b) Calculate the maximum distance of the projectile from the centre of the earth during its course of motion.
View SolutionA tunnel ois dug along a chord of the earth a perpendicular distance R2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the eall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View Solution
