Assume that an electric field →E=30x2ˆi exists in space. Then the potential differences VA−V0 where V0 is the potential at the origin and VA, the potential at x=2m is
120 V
−120V
−80V
80V
The correct Answer is:C
To find the potential difference VA−V0 where V0 is the potential at the origin and VA is the potential at x=2m, we can follow these steps:
Step 1: Understand the relationship between electric field and potential
The potential difference dV between two points in an electric field is given by:
dV=−→E⋅d→x
where →E is the electric field and d→x is the displacement vector.
Step 2: Set up the integral for potential difference
To find the potential difference VA−V0, we need to integrate the expression from the origin (0) to the point at x=2m:
VA−V0=−∫20→E⋅d→x
Step 3: Substitute the electric field
Given that the electric field is →E=30x2^i, the displacement vector in the x direction can be expressed as d→x=dx^i. Therefore, the dot product becomes:
→E⋅d→x=(30x2^i)⋅(dx^i)=30x2dx
Step 4: Set up the integral
Now we can rewrite the integral:
VA−V0=−∫2030x2dx
Step 5: Calculate the integral
Now we compute the integral:
∫30x2dx=30⋅x33=10x3
Evaluating this from 0 to 2:
VA−V0=−(10x3)20=−(10(23)−10(03))=−(10⋅8−0)=−80
Step 6: Final result
Thus, the potential difference VA−V0 is:
VA−V0=−80V
Summary
The potential difference VA−V0 is −80V.
---
The potential difference dV between two points in an electric field is given by:
dV=−→E⋅d→x
where →E is the electric field and d→x is the displacement vector.
To find the potential difference VA−V0, we need to integrate the expression from the origin (0) to the point at x=2m:
VA−V0=−∫20→E⋅d→x
Given that the electric field is →E=30x2^i, the displacement vector in the x direction can be expressed as d→x=dx^i. Therefore, the dot product becomes:
→E⋅d→x=(30x2^i)⋅(dx^i)=30x2dx
Now we can rewrite the integral:
VA−V0=−∫2030x2dx
Now we compute the integral:
∫30x2dx=30⋅x33=10x3
Evaluating this from 0 to 2:
VA−V0=−(10x3)20=−(10(23)−10(03))=−(10⋅8−0)=−80
Thus, the potential difference VA−V0 is:
VA−V0=−80V
The potential difference VA−V0 is −80V.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Knowledge Check
The potential field of an electric field →E=(yˆi+xˆj) is
AV = -(x+y) + constantBV = constantCV=−(x2+y2)+ constantDV = -xy + constant
An electric field →E=Bxˆi exists in space, where B=20V/m2. Taking the potential at (2m, 4m) to be zero, find the potential at the origin.
View SolutionPotential difference VB−VA in the network shown is
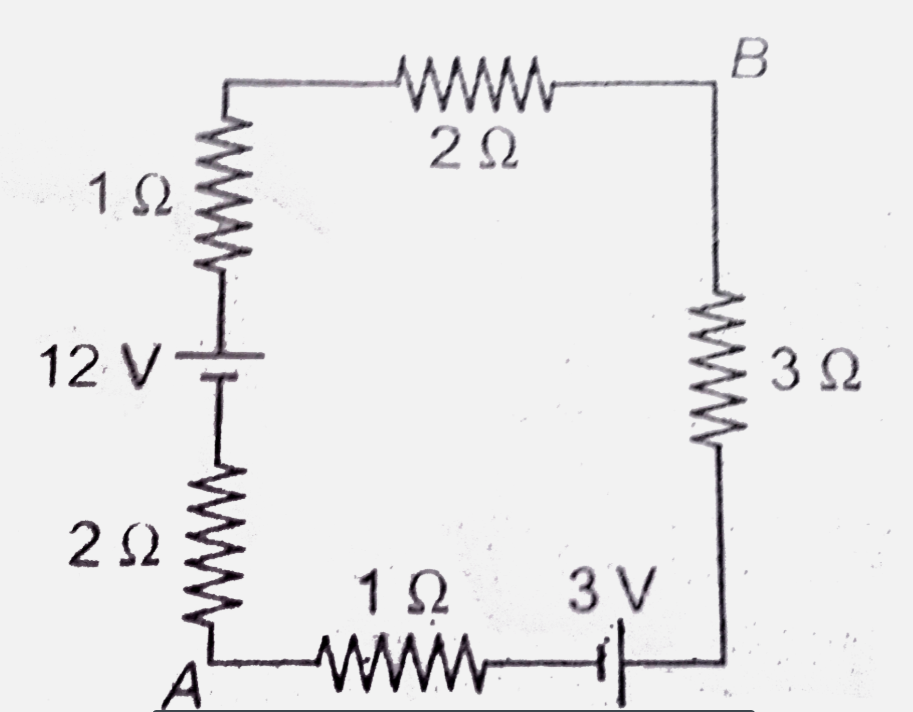
View SolutionAn electric field →E=→IAx exists in the space, where A=10Vm−2. Take the potential at (10m, 20m ) to be zero. Find the potential at the origin.
View SolutionPotential difference across AB , i.e., VA−VB is

View SolutionAn electric field →E=−−−−−−−→i20+→j30NC−1 exists in the space. If the potential at the origin is taken to be zero find the potential at (2m, 2m).
View SolutionThe potential field of an electric field →E=(yˆi+xˆj) is
View SolutionIn the given circuit find the |VA−VB| where VA,VB are electric potentials at the points A and B.

View Solution

 .
.