Assume that as narrow tunnel is dug between two diametrically opposite points of the earth. Treat the earth as a solid sphere of uniform density. Show that if a particle is released in this tunnel, it will execute a simple harmonic motion. Calculate the time period of this motion.
To solve the problem, we will follow these steps:
Step 1: Understand the Setup
We have a narrow tunnel dug between two diametrically opposite points of the Earth. We will treat the Earth as a solid sphere with uniform density.
Step 2: Define the Variables
Let:
- R = radius of the Earth
- x = distance from the center of the Earth to the particle in the tunnel
Step 3: Determine the Mass Inside the Radius
Using the concept of uniform density, the mass m of the Earth can be expressed as:
m=ρ⋅V
where V is the volume of the sphere of radius x:
V=43πx3
Thus, the mass mx of the Earth within radius x is:
mx=ρ⋅43πx3
Step 4: Calculate the Gravitational Force
The gravitational force acting on the particle when it is at distance x from the center is given by:
F=−Gmxmx2
Substituting mx:
F=−G(ρ⋅43πx3)mx2
This simplifies to:
F=−43πGρmx
Step 5: Identify the Simple Harmonic Motion
The force can be expressed in the form of Hooke's law:
F=−kx
where k=43πGρm. This indicates that the motion is simple harmonic since the force is proportional to the displacement and directed towards the equilibrium position.
Step 6: Calculate the Time Period
The time period T of simple harmonic motion is given by:
T=2π√mk
Substituting the value of k:
T=2π√m43πGρm
The mass m cancels out:
T=2π
⎷143πGρ=2π√34πGρ
Step 7: Substitute Density of Earth
The average density of the Earth ρ can be approximated as:
ρ≈5500kg/m3
Thus, substituting this value gives:
T=2π√34πG⋅5500
Step 8: Final Calculation
Using G≈6.674×10−11m3/kg⋅s2:
T≈2π√34π⋅6.674×10−11⋅5500
Calculating this will yield the time period of the simple harmonic motion.
Final Result
After performing the calculations, you will find that the time period T is approximately 84.5 minutes.
---
We have a narrow tunnel dug between two diametrically opposite points of the Earth. We will treat the Earth as a solid sphere with uniform density.
Let:
- R = radius of the Earth
- x = distance from the center of the Earth to the particle in the tunnel
Using the concept of uniform density, the mass m of the Earth can be expressed as:
m=ρ⋅V
where V is the volume of the sphere of radius x:
V=43πx3
Thus, the mass mx of the Earth within radius x is:
mx=ρ⋅43πx3
The gravitational force acting on the particle when it is at distance x from the center is given by:
F=−Gmxmx2
Substituting mx:
F=−G(ρ⋅43πx3)mx2
This simplifies to:
F=−43πGρmx
The force can be expressed in the form of Hooke's law:
F=−kx
where k=43πGρm. This indicates that the motion is simple harmonic since the force is proportional to the displacement and directed towards the equilibrium position.
The time period T of simple harmonic motion is given by:
T=2π√mk
Substituting the value of k:
T=2π√m43πGρm
The mass m cancels out:
T=2π
⎷143πGρ=2π√34πGρ
The average density of the Earth ρ can be approximated as:
ρ≈5500kg/m3
Thus, substituting this value gives:
T=2π√34πG⋅5500
Using G≈6.674×10−11m3/kg⋅s2:
T≈2π√34π⋅6.674×10−11⋅5500
Calculating this will yield the time period of the simple harmonic motion.
After performing the calculations, you will find that the time period T is approximately 84.5 minutes.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective -1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
Consider the situastion shown in figure. Show that if that blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.
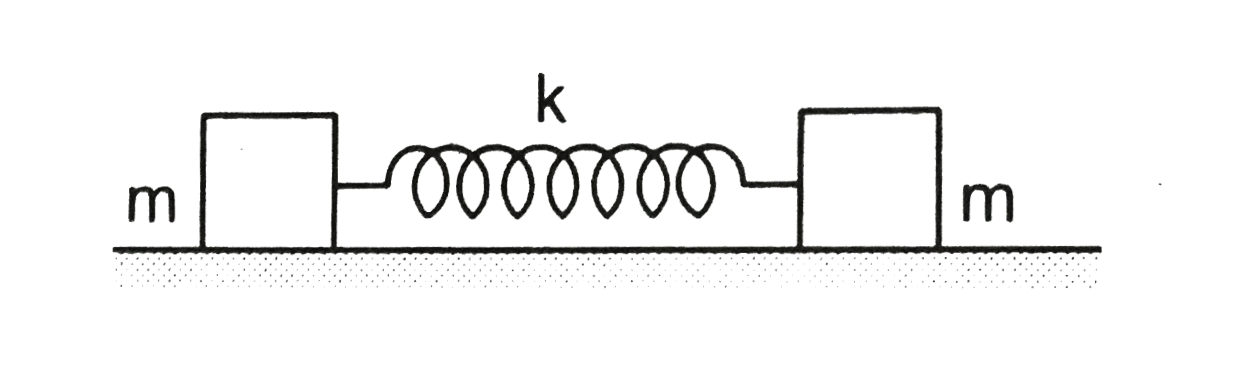
View SolutionConsider the situation shown in figure. Show that if the blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.

View Solution
Knowledge Check
A particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
ATB2TC4TDT2
Imagine a narrow tunnel between the two diametrically opposite points of the earth. A particle of mass m is released in this tunnel . The time period of oscillation is
View SolutionA cubical wood piece of mass 13.5 gm and volume 0.0027m3 float in water. It is depressed and released, then it executes simple harmonic motion. Calculate the period of oscillation ?
View SolutionAssume that a tunnel is dug through earth from North pole to south pole and that the earth is a non-rotating, uniform sphere of density ρ. The gravitational force on a particle of mass m dropped into the tunnel when it reaches a distance r from the centre of earth is
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Time period of the particle is not equal to
View SolutionIf the earth was a homogeneous sphere and a straight hole was bored through its centre, show that a body dropped into this hole will execute shm. Calculate the time period if the radius of the earth is 6400 km and g = 9.8ms−2
View SolutionSuppose a vertical tunnel is dug along the diameter of earth , which is assumed to be a sphere of uniform mass density ρ. If a body of mass m is thrown in this tunnel, its acceleration at a distance y from the centre is given by

View SolutionSuppose a verticle tunnel is dug along the diametal of earth , which is assumed to be a sphere of unifrom mass density ρ. If a body of mass m is throws in this tunal, its acceleration at a distance y from the centre is given by

View Solution
