Assume that if the shear stress in steel exceeds about 4.00×108N/m2 the steel ruptures. Determine the shearing force necessary to (a) shear a steel bolt 1.00cm in diameter and (b) punch a 1.00cm diameter hole in a steel plate 0.500cm thick.
To solve the problem of determining the shearing force necessary to shear a steel bolt and punch a hole in a steel plate, we will follow these steps:
Given Data:
- Shear stress limit for steel, σ=4.00×108N/m2
- Diameter of the bolt and hole, d=1.00cm=1.00×10−2m
- Thickness of the plate, t=0.500cm=0.500×10−2m
(a) Shearing Force to Shear a Steel Bolt
1. Calculate the Area of the Bolt:
The cross-sectional area A of the bolt can be calculated using the formula for the area of a circle:
A=π4d2
Substituting the diameter:
A=π4(1.00×10−2)2=π4×1.00×10−4m2
2. Calculate the Shearing Force:
The shearing force F can be calculated using the formula:
F=σ×A
Substituting the values:
F=4.00×108N/m2×π4×1.00×10−4m2
Simplifying this gives:
F=4.00×108×3.144×1.00×10−4
F=3.14×104N
(b) Shearing Force to Punch a Hole in a Steel Plate
1. Calculate the Circumference of the Hole:
The circumference C of the hole is given by:
C=πd
Substituting the diameter:
C=π×(1.00×10−2)m
2. Calculate the Area of Shear:
The area A on which the shear force acts is the product of the circumference and the thickness of the plate:
A=C×t=πd×t
Substituting the values:
A=π×(1.00×10−2)×(0.500×10−2)m2
3. Calculate the Shearing Force:
Again, using the formula F=σ×A:
F=4.00×108N/m2×π×(1.00×10−2)×(0.500×10−2)
Simplifying this gives:
F=4.00×108×π×5.00×10−5
F=6.28×104N
Final Answers:
- (a) Shearing force necessary to shear the steel bolt: F=3.14×104N
- (b) Shearing force necessary to punch a hole in the steel plate: F=6.28×104N
- Shear stress limit for steel, σ=4.00×108N/m2
- Diameter of the bolt and hole, d=1.00cm=1.00×10−2m
- Thickness of the plate, t=0.500cm=0.500×10−2m
The cross-sectional area A of the bolt can be calculated using the formula for the area of a circle:
A=π4d2
Substituting the diameter:
A=π4(1.00×10−2)2=π4×1.00×10−4m2
The shearing force F can be calculated using the formula:
F=σ×A
Substituting the values:
F=4.00×108N/m2×π4×1.00×10−4m2
Simplifying this gives:
F=4.00×108×3.144×1.00×10−4
F=3.14×104N
The circumference C of the hole is given by:
C=πd
Substituting the diameter:
C=π×(1.00×10−2)m
The area A on which the shear force acts is the product of the circumference and the thickness of the plate:
A=C×t=πd×t
Substituting the values:
A=π×(1.00×10−2)×(0.500×10−2)m2
Again, using the formula F=σ×A:
F=4.00×108N/m2×π×(1.00×10−2)×(0.500×10−2)
Simplifying this gives:
F=4.00×108×π×5.00×10−5
F=6.28×104N
- (a) Shearing force necessary to shear the steel bolt: F=3.14×104N
- (b) Shearing force necessary to punch a hole in the steel plate: F=6.28×104N
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Solved Examples
Explore 11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Exercise 5.1
Explore 12 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
The breaking stress of steel is 7.85×108N/m2 and density of steel is 7.7×103kg/m3. The maximum frequency to which a string 1m long can be tuned is
View SolutionThe area of cross section of a steel wire (Y=2.0×1011N/m2) is 0.1cm2. The force required to double is length will be
View SolutionYoung 's modulus of steel is 2.0×1011Nm/(2). Express it is dynecm2.
View SolutionA steel wire of diameter 2 mm has a breaking strength of 4×105N. What is the breaking strength of similar steel wire of diameter 1.5mm ?
View SolutionA steel wire of diameter 2 mm has a breaking strength of 4×105N. What is the breaking strength of similar steel wire of diameter 1.5mm ?
View SolutionThe elastic limit of a steel cable is 3.0×108N/m2 and the cross-section area is 4cm2. Find the maximum upward acceleration that can be given to a 900kg elevator supported by the cable if the stress is not to exceed one - third of the elastic limit.
View SolutionFind the number of coins, 1.5 cm in diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
View SolutionFind the number of coins, 1.5 cm in diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
View Solutiona. Estimate the force with which a karate master strikes a board, assuming that hand's speed at the moment of impact is 10.0ms−1, decreasing to 1.00ms−1 during a 0.002s time interval of contact between the hand and the board. The mass of his hand and arm is 1.00kg .
b Estimate the shear, assuming this force it exerted on a 1.00cm thick pine board that is 10.0cm wide.
c. If we maximum shear stress a pine board can support before breaking is 3.60×106N/m2, will the board break?
View SolutionSuppose the object in figure shown is the brass plate of an outdoor sculpture. It experiences shear forces as a result of an erthquake. The frame is 0.80 m and 0.50 cm thick. Calculate the shear strain produced in this object if the displacement x is 0.16 mm. (Shear modulus =3.5×1010Pa)
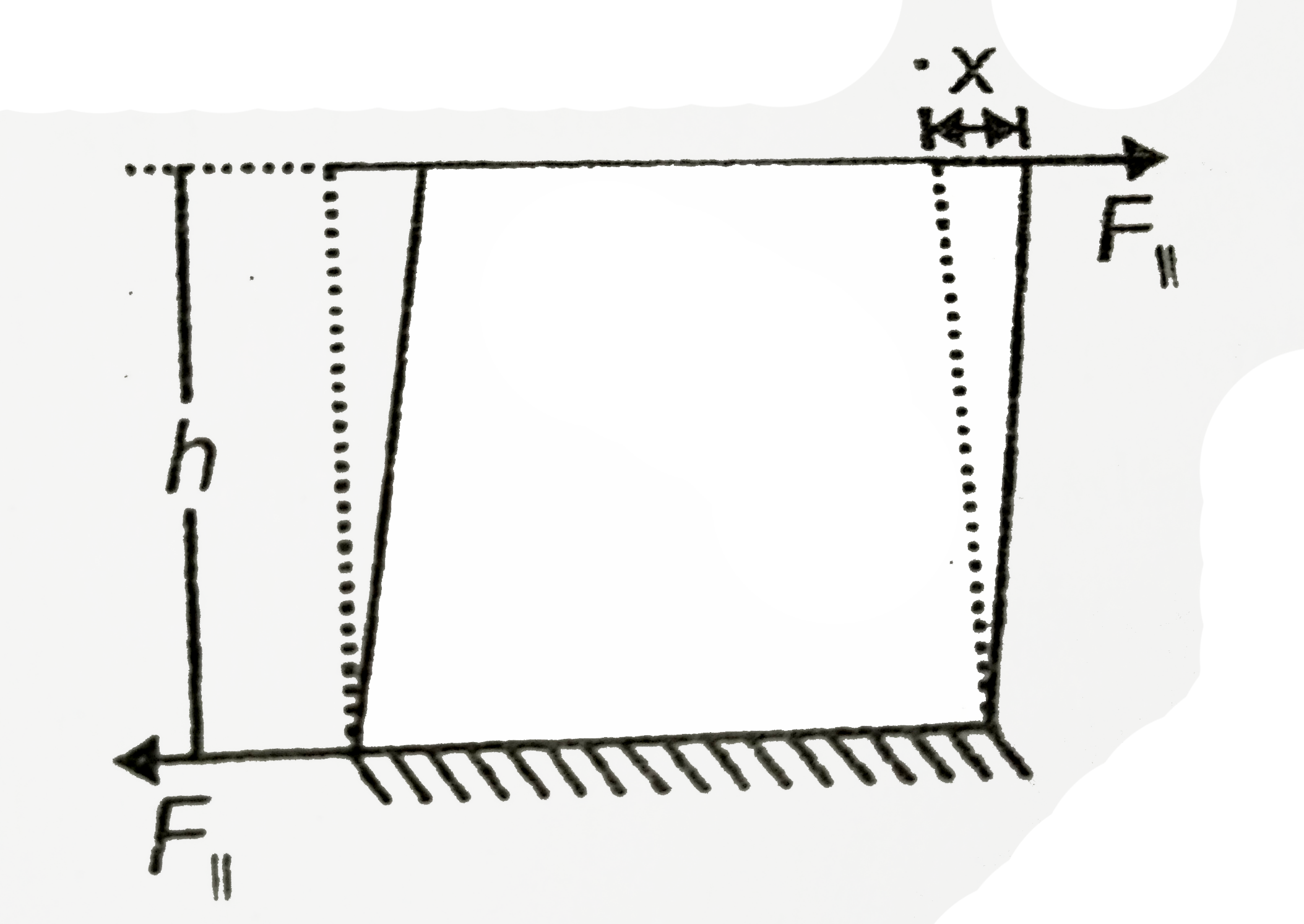
View Solution
