Assume that there is a tunnel in the shape of a circular arc through the earth. Wall of the tunnel is smooth. A ball of mass m is projected into the tunnel at A with speed v. The all comes out of the tunnel at B and escapes out of the gravity of the earth. Mass and radius of the earth are M and R respectively and radius of the circle shaped tunnel is also . Find minimum possible value of v (call it v0) If the ball is projected into the tunnel with speed v0, calculate the normal force applied by the tunnel wall on the ball when it is closest to the centre of the earth. It is given that the closest distance between the ball and the centre of the earth is R2

The correct Answer is:(a)v0=√2GMR
(b) 274GMmR2
Step by step video, text & image solution for Assume that there is a tunnel in the shape of a circular arc through the earth. Wall of the tunnel is smooth. A ball of mass m is projected into the tunnel at A with speed v. The all comes out of the tunnel at B and escapes out of the gravity of the earth. Mass and radius of the earth are M and R respectively and radius of the circle shaped tunnel is also . Find minimum possible value of v (call it v_(0)) If the ball is projected into the tunnel with speed v_(0), calculate the normal force applied by the tunnel wall on the ball when it is closest to the centre of the earth. It is given that the closest distance between the ball and the centre of the earth is (R)/(2) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
We know that the atmospheric pressure on the surface of the earth is because of weight, of the air. The radius of the earth is 6400 km and atmospheric pressure on the sruface of earth is 1×105N/m2. Estimate the mass of the earth's atmosphere assuming that acceleration due to gravity remains constant at 10m/s2 over the entrie height of the atmospehre.
View SolutionFour metal rods each of length L and cross sectional area A are joined at point M. Thermal conductivities of MA, MB and MD are equal and that of MC is thrice that of MA. The end points A, B, C and D are kept in large reservoirs. Heat folws into the junction from B at a rate of P(Js−1) and C from at a rate of 3P. Heat flows out of D at a rate of 5P.
(a) Find the relation between temperatures of points A, B and C.
(b) Find temperature of D if temperature of A and M and TA and TM respectively.
View SolutionAssume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of √(gR) (b) it is relased from a height R above the tunnel (c ) it is thrown vertically upward along the length of tunnel with a speed of √gR.
View SolutionMotion Of A Ball In A Tunnel Through The Earth
View SolutionA smooth tunnel is dug along the radius of earth that ends at centre. A ball is relrased from the surface of earth along tunnel. Caefficient of restitution for collision between soil at centre and ball is 0.5 . Caculate the distance travelled by ball just second collision at center. Given mass of the earth is M and radius of the earth is R .
View SolutionA tunnel is dug inside the earth across one of its diameters. Radius of earth is R and its mass is M. A particle is projected inside the tunnel with velocity sqrt((2GM)/(R)) from one of its ends then maximum velocit attained by the particle in the subsequent motion is sqrt((nGM)/(R)) (assuming tunnel to be frictionless). Find n
View SolutionA tunnel is dug across the diameter of earth. A ball is released from the surface of Earth into the tunnel. The velocity of ball when it is at a distance R2 from centre of earth is (where R = radius of Earth and M = mass of Earth)
View SolutionA ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
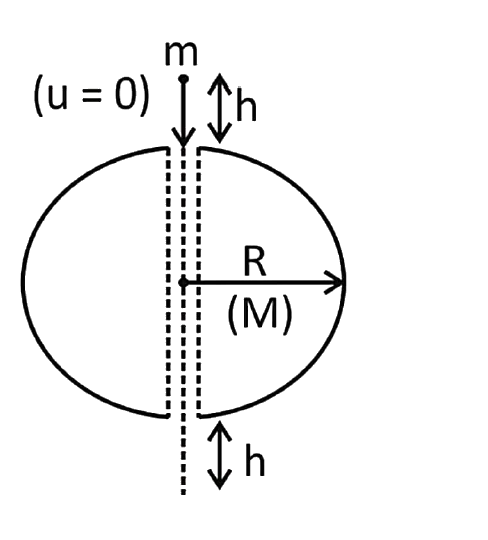
View SolutionAfter drilling a tunnel from surface of earth to the centre, a body of mass m is dropped into the tunnel. Calculate the speed with which the body strikes the bottom of tunnel. Here, M is the mass of earth and R is radius of earth.
View SolutionConsider the motion of a ball in a tunnel through the earth (radius of the earth is R and mass of the earth is M), the tunnel is along a chord and the ball is released from the surface. The time period of the ball is √x (approx), find x.
View SolutionAssume that a tunnel is dug along a cord of earth at a perpendicular distance R/2 from earth's centre where R is the radius of earth. The wall of tunnel is frictionless. Find the time period of particle excuting SHM in tunnel
View SolutionA tunnel is dug along a diameter of earth. IF M is mass of the earth, then force on a particle of mass m placed in that tunnel at a distance x from the centre is
View SolutionA smooth tunnel is dug along the radius of earth that ends at centre. A ball is relrased from the surface of earth along tunnel. Caefficient of restitution for collision between soil at centre and ball is 0.5. Caculate the distance travelled by ball just second collision at center. Given mass of the earth is M and radius of the earth is R.
View Solutionत्रिज्या R व द्रव्यमान M की पृथ्वी के व्यास के अनुदिश एक सुरंग बनाई जाती है। सुरंग के केन्द्र पर 'm' दव्यमान का एक कण है। वह न्यूनतम वेग जिसको देने से कण पृथ्वी की सतह पर पहुँचें, होगा
View SolutionAssume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of √(gR) (b) it is relased from a height R above the tunnel (c ) it is thrown vertically upward along the length of tunnel with a speed of √gR.
View Solution
