At , the value of the density of a fixed mass of an ideal gas divided by its pressure is x. at , this ratio is
x
The correct Answer is:D
To solve the problem, we need to find the ratio of the density of a fixed mass of an ideal gas to its pressure at two different temperatures. Let's break it down step by step.
Step 1: Understand the Ideal Gas Law
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = Pressure
- V = Volume
- n = Number of moles
- R = Universal gas constant
- T = Temperature in Kelvin
Step 2: Relate Density to Pressure and Temperature
Density (ρ) can be expressed as:
ρ=mV
Where m is the mass of the gas. From the ideal gas law, we can express density in terms of pressure and temperature:
ρ=P⋅MR⋅T
Where M is the molar mass of the gas.
Step 3: Find the Ratio of Density to Pressure
From the above equation, we can derive the ratio of density to pressure:
ρP=MR⋅T
This means that the ratio of density to pressure is directly proportional to the molar mass and inversely proportional to the temperature.
Step 4: Calculate the Ratio at Two Different Temperatures
Let x be the ratio at 10∘C:
x=MR⋅T1
Where T1=10+273=283K.
Now, at 110∘C, let the new ratio be x′:
x′=MR⋅T2
Where T2=110+273=383K.
Step 5: Express the New Ratio in Terms of x
We can relate x′ to x:
x′x=T1T2
Substituting the values of T1 and T2:
x′x=283383
Thus, we can express x′ as:
x′=x⋅283383
Conclusion
The ratio of the density of the gas to its pressure at 110∘C is:
x′=283383⋅x
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = Pressure
- V = Volume
- n = Number of moles
- R = Universal gas constant
- T = Temperature in Kelvin
Density (ρ) can be expressed as:
ρ=mV
Where m is the mass of the gas. From the ideal gas law, we can express density in terms of pressure and temperature:
ρ=P⋅MR⋅T
Where M is the molar mass of the gas.
From the above equation, we can derive the ratio of density to pressure:
ρP=MR⋅T
This means that the ratio of density to pressure is directly proportional to the molar mass and inversely proportional to the temperature.
Let x be the ratio at 10∘C:
x=MR⋅T1
Where T1=10+273=283K.
x′=MR⋅T2
Where T2=110+273=383K.
We can relate x′ to x:
x′x=T1T2
Substituting the values of T1 and T2:
x′x=283383
Thus, we can express x′ as:
x′=x⋅283383
The ratio of the density of the gas to its pressure at 110∘C is:
x′=283383⋅x
Topper's Solved these Questions
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Multiple choice questions-II
8 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Multiple choice questions-III
12 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Problems for practice
47 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
Similar Questions
Knowledge Check
At 10∘C, the density of a fixed mass of an ideal gas divided by its pressure is X. At 110∘C, this ratio would be
A10x110B283x383CxD383283 XA 0∘C the density of a fixed mass of a gas divided by pressure is x. At 100∘C, the ratio will be
AxB273373xC373273xD100273xFor a fixed mass of an ideal gas the correct representation is:
A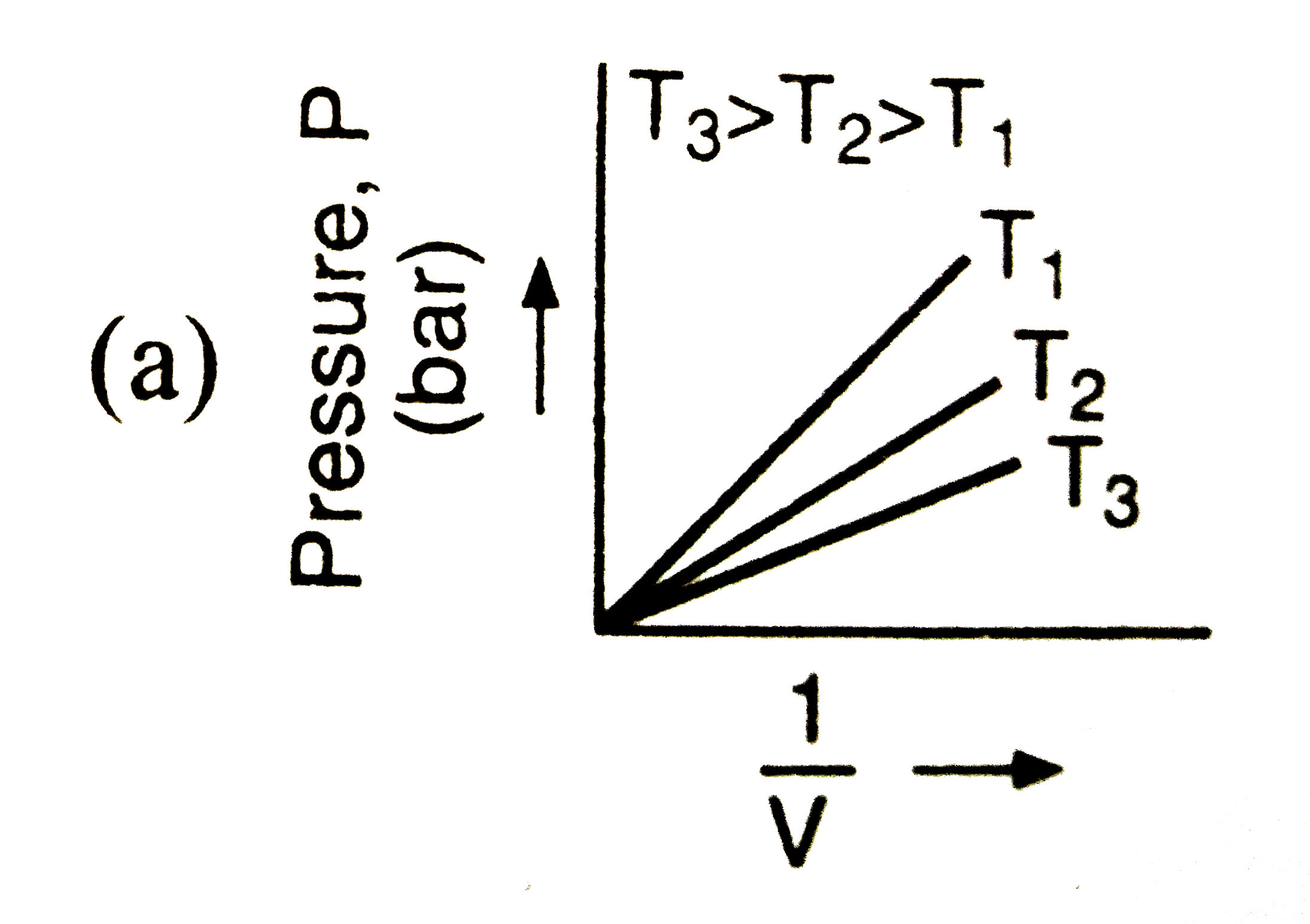 B
B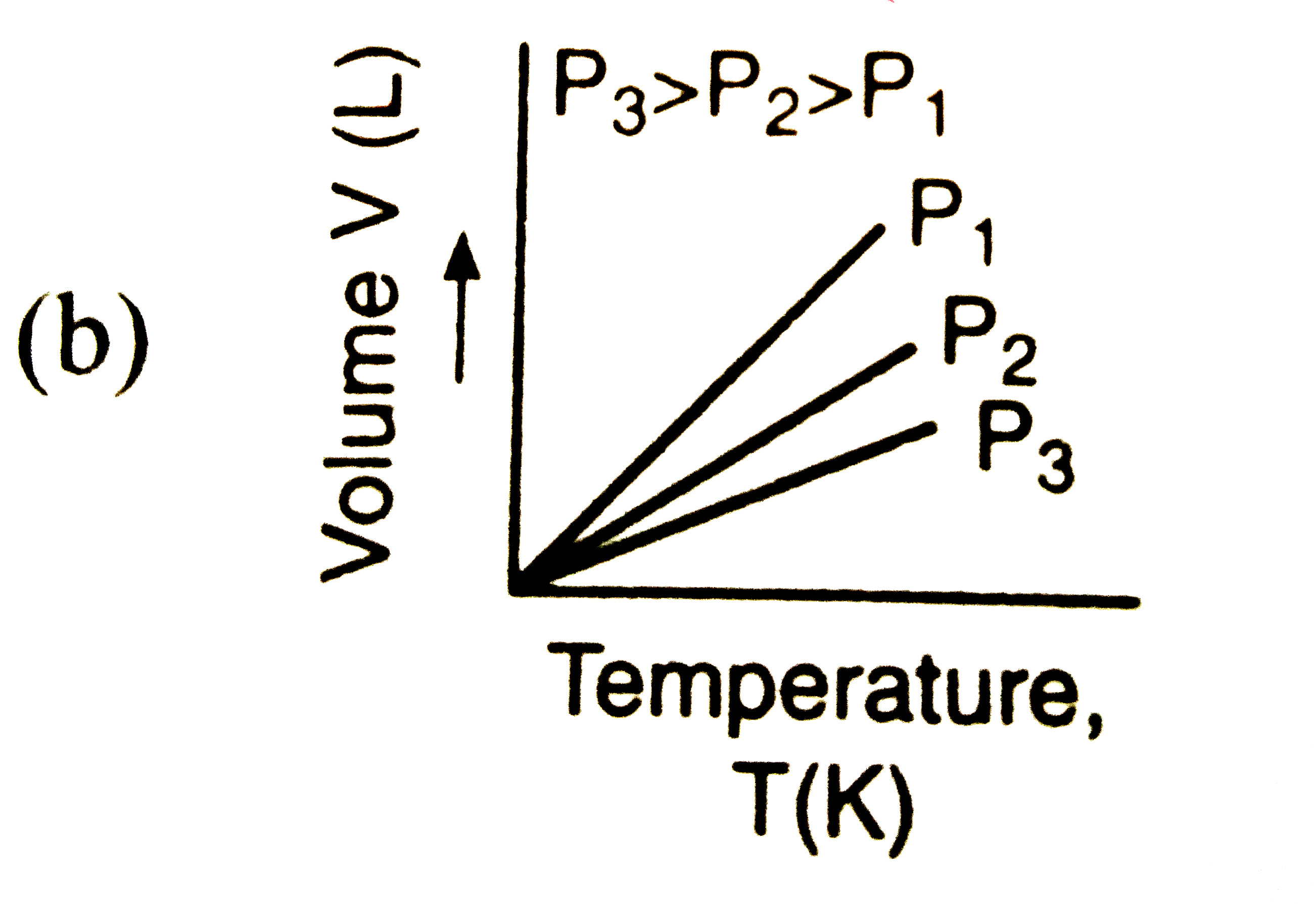 C
C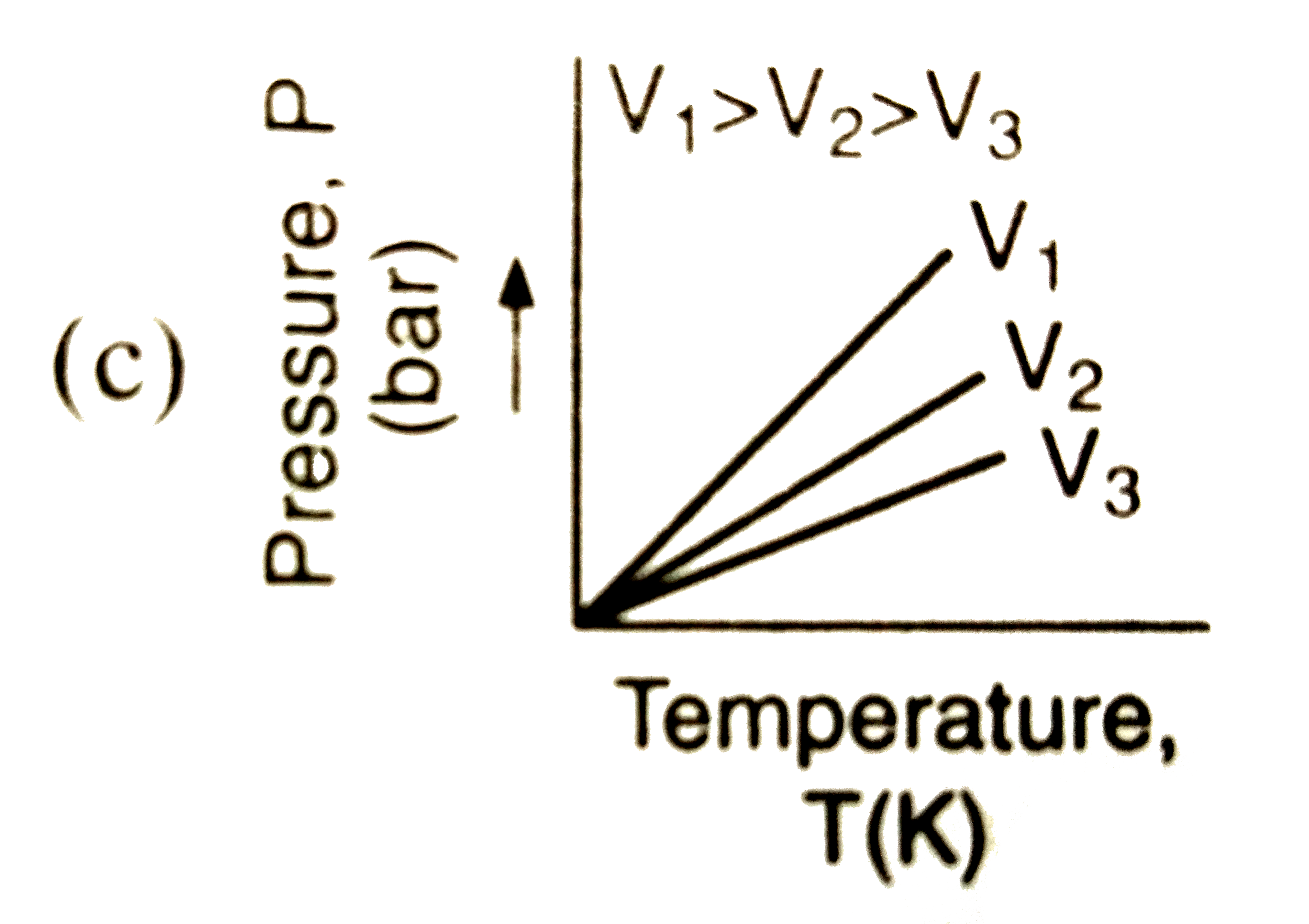 D
D
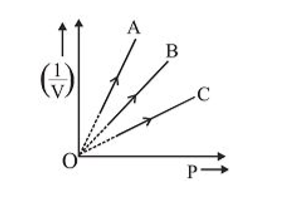
Figure shows the isotherms of fixed mass of an ideal gas at three temperatures TA.TB and TC then:-
View SolutionThe energy density uV of an ideal gas is related to its pressure P as
View SolutionThe ratio of the density and pressure of a fixed mass of an ideal gas is "5" at 10°C. Then this ratio at 110°C is
View SolutionAt constant pressure , the volume of fixed mass of an ideal gas is directly proportional to
View SolutionIf E is the energy density in an ideal gas, then the pressure of the ideal gas is
View Solution