At t=0, the displacement x(0) of the block in a linear oscillator like that of Fig . 15.5 is −8.50cm. (Read x(0) as ''x at time zero'') The block's velocity v(0) then is −0.920m/s, and its acceleration a(0) is +47.0m/s2.
What are the phase constant ϕ and amplitude xm?
Calculations: We know ω and want ϕandxm. If we divide Eq.15.18 by Eq.15.17, we eliminate one of those unknowns and reduce the other to a single trignometric function:
v(0)x(0)=−ωxmsinϕxmcosϕ=−ωtanϕ
Solving for tanϕ, we find
tanϕ=−v(0)ωx(0)=−−0.920m/s(23.5rad/s)(−0.0850m)
=−0.461
This equation has two solutions:
ϕ=−25∘andϕ=−180∘+(−25∘)=155∘.
Normally only the first solution here is displayed by a calculator, but it may not be the physically possible solution. To choose the proper solution, we test them both by using them to compute values for the amplitude xm. From Eq. 15.17, we find if ϕ=−25∘, then
xm=x(0)cosϕ=−0.0850mcos(−25∘)=−0.094m
We find similarly that if ϕ=−155∘,then xm=0.094m. Because the amplitude of SHM must be positive constant, the correct phase constant and amplitude here are
ϕ=−155∘andxm=0.094m=9.4cm
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint8videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems39videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)4videos
PHOTONS AND MATTER WAVES
Similar Questions
At t=0, the displacement x(0) of the block in a linear oscillator like that of Fig. 15.5 is −8.50cm. (Read x(0) as ''x at time zero''). The block's velocity v(0) then is −0.920m/s, and its acceleration a(0) is +47.0m/s2.
What is the phase constant ϕ and amplitude xm ?View SolutionAt t=0, the displacement x(0) of the block in a linear oscillator like that of Fig . 15.5 is −8.50cm. (Read x(0) as ''x at time zero'') The block's velocity v(0) then is −0.920m/s, and its acceleration a(0) is +47.0m/s2.
What is the angular frequency ω of this system?View Solution
Knowledge Check
- Question 1 - Select One
The maximum velocity for particle in SHM is 0.16 m/s and maximum acceleration is 0.64m/s2. The amplitude is
A4×10−2mB4×10−1mC4×10mD4×100m
At t=0, the displacement x(0) of the block in a linear oscillator like that of Fig. 15.5 is −8.50cm. (Read x(0) as ''x at time zero''). The block's velocity v(0) then is −0.920m/s, and its acceleration a(0) is +47.0m/s2.
What is the angular frequency ω of this system?View SolutionIf the position of the block in a block-spring oscillator is given by
x(t)=(3.00×10−3m)cos[(4.00rad/s)t+0.120rad], what is the block's position, velocity and acceleration at time t= 2.30s?View SolutionA body oscillates with a simple harmonic motion having amplitude 0.05 m. At a certain instant of time, its displacement is 0.01 m and acceleration is 1.0m/s2. The period of oscillation is
View SolutionThe velocity of an object at t =0 is →v0=−4ˆj m/s . It moves in plane with constant acceleration →a=(3ˆi+8ˆj)m/s2. What is its velocity after 1 s?
View SolutionThe velocity of an object at t =0 is →v0=−4ˆj m/s . It moves in plane with constant acceleration →a=(3ˆi+8ˆj)m/s2. What is its velocity after 1 s?
View SolutionFor a particular transverse standing wave on a long string, one of the antinodes is at r=0 and an adjacent node is at x=0.10 m. The displacement y(t) of the string particle at x =0 is shown in Fig. 16-40, where the scale of the y axis is set by ys=4.0cm. When t = 0.50 s, what is the displacement of the string particle at (a) x= 0.20 m and (b) x= 0.30 m? What is the transverse velocity of the string particle at x =0.20 m at (c) t=0.50s and (d) t=1.0s? (e) Sketch the standing wave at t=0.50s for the range x=0 to x=0.40m.
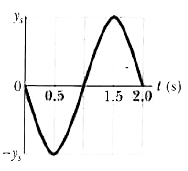View SolutionA particle confined to motion along an x axis moves with constant acceleration from x=2.0m to x=8.0 m during a 2.5 s time interval. The velocity of the particle at x=8.0m is 2.8 m/s. What is the constant acceleration during this time interval ?
View Solution