At t=0, the displacement x(0) of the block in a linear oscillator like that of Fig. 15.5 is −8.50cm. (Read x(0) as ''x at time zero''). The block's velocity v(0) then is −0.920m/s, and its acceleration a(0) is +47.0m/s2.
What is the phase constant ϕ and amplitude xm ?
Calculations: We know ω and want ϕandxm. If we divide Eq. 15.26 by Eq. 15.25, we find
v(0)x(0)=−ωxmsinϕxmcosϕ
Solving for tanϕ, we find
tanϕ=−v(0)ωx(0)=−−0.920m/s(23.5rad/s)(−0.0850m)
This equation has two solutions:
ϕ=−25∘andϕ=180∘+(−25∘)=155∘
(Normally, only the first solution here is displayed by a calculator), To choose the proper solution, we test them both by using them to compute values for the amplitude xm, From Eq. 15.25, we find that if ϕ=−25∘, then
xm=x(0)cosϕ=−0.0850mcos(−25∘)=−0.094m
We find similarly that if ϕ=155∘, then xm=0.094m. Because the amplitude of SHM must be a positive constant, the correct phase constant and amplitude here are
ϕ=155∘andxm=0.094m=9.4cm
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint8videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems39videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)4videos
PHOTONS AND MATTER WAVES
Similar Questions
At t=0, the displacement x(0) of the block in a linear oscillator like that of Fig . 15.5 is −8.50cm. (Read x(0) as ''x at time zero'') The block's velocity v(0) then is −0.920m/s, and its acceleration a(0) is +47.0m/s2.
What are the phase constant ϕ and amplitude xm?View SolutionAt t=0, the displacement x(0) of the block in a linear oscillator like that of Fig. 15.5 is −8.50cm. (Read x(0) as ''x at time zero''). The block's velocity v(0) then is −0.920m/s, and its acceleration a(0) is +47.0m/s2.
What is the angular frequency ω of this system?View Solution
Knowledge Check
- Question 1 - Select One
The maximum velocity for particle in SHM is 0.16 m/s and maximum acceleration is 0.64m/s2. The amplitude is
A4×10−2mB4×10−1mC4×10mD4×100m
At t=0, the displacement x(0) of the block in a linear oscillator like that of Fig . 15.5 is −8.50cm. (Read x(0) as ''x at time zero'') The block's velocity v(0) then is −0.920m/s, and its acceleration a(0) is +47.0m/s2.
What is the angular frequency ω of this system?View SolutionIf the position of the block in a block-spring oscillator is given by
x(t)=(3.00×10−3m)cos[(4.00rad/s)t+0.120rad], what is the block's position, velocity and acceleration at time t= 2.30s?View SolutionA body oscillates with a simple harmonic motion having amplitude 0.05 m. At a certain instant of time, its displacement is 0.01 m and acceleration is 1.0m/s2. The period of oscillation is
View SolutionThe velocity of an object at t =0 is →v0=−4ˆj m/s . It moves in plane with constant acceleration →a=(3ˆi+8ˆj)m/s2. What is its velocity after 1 s?
View SolutionThe velocity of an object at t =0 is →v0=−4ˆj m/s . It moves in plane with constant acceleration →a=(3ˆi+8ˆj)m/s2. What is its velocity after 1 s?
View SolutionFor a particular transverse standing wave on a long string, one of the antinodes is at r=0 and an adjacent node is at x=0.10 m. The displacement y(t) of the string particle at x =0 is shown in Fig. 16-40, where the scale of the y axis is set by ys=4.0cm. When t = 0.50 s, what is the displacement of the string particle at (a) x= 0.20 m and (b) x= 0.30 m? What is the transverse velocity of the string particle at x =0.20 m at (c) t=0.50s and (d) t=1.0s? (e) Sketch the standing wave at t=0.50s for the range x=0 to x=0.40m.
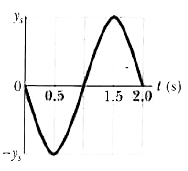 View Solution
View SolutionA particle confined to motion along an x axis moves with constant acceleration from x=2.0m to x=8.0 m during a 2.5 s time interval. The velocity of the particle at x=8.0m is 2.8 m/s. What is the constant acceleration during this time interval ?
View Solution

