At the surface of earth, potential energy of a particle is U and potential is V.Change in potential energy and potential at height h=R are suppose ΔU and ΔV.Then
ΔU=−U/2
ΔU=U/2
ΔV=V/2
ΔV=−V/2
The correct Answer is:A, D
To solve the problem, we need to find the change in potential energy (ΔU) and the change in potential (ΔV) of a particle when it is moved from the surface of the Earth to a height equal to the radius of the Earth (h = R).
1. Identify the Given Variables:
- At the surface of the Earth:
- Potential energy (U) = −GMmR
- Potential (V) = −GMR
- At height h=R:
- The distance from the center of the Earth to the particle is R+R=2R.
2. Calculate Potential Energy at Height h=R:
- The potential energy at height h (U1) is given by:
U1=−GMm2R
3. Calculate the Change in Potential Energy (ΔU):
- The change in potential energy is given by:
ΔU=U1−U
- Substituting the values:
ΔU=(−GMm2R)−(−GMmR)
- Simplifying:
ΔU=−GMm2R+GMmR=GMmR−GMm2R=GMm2R
- Thus:
ΔU=−U2
4. Calculate Potential at Height h=R:
- The potential at height h (V1) is given by:
V1=−GM2R
5. Calculate the Change in Potential (ΔV):
- The change in potential is given by:
ΔV=V1−V
- Substituting the values:
ΔV=(−GM2R)−(−GMR)
- Simplifying:
ΔV=−GM2R+GMR=GMR−GM2R=GM2R
- Thus:
ΔV=−V2
Final Results:
- Change in potential energy: ΔU=−U2
- Change in potential: ΔV=−V2
- At the surface of the Earth:
- Potential energy (U) = −GMmR
- Potential (V) = −GMR
- At height h=R:
- The distance from the center of the Earth to the particle is R+R=2R.
- The potential energy at height h (U1) is given by:
U1=−GMm2R
- The change in potential energy is given by:
ΔU=U1−U
- Substituting the values:
ΔU=(−GMm2R)−(−GMmR)
- Simplifying:
ΔU=−GMm2R+GMmR=GMmR−GMm2R=GMm2R
- Thus:
ΔU=−U2
- The potential at height h (V1) is given by:
V1=−GM2R
- The change in potential is given by:
ΔV=V1−V
- Substituting the values:
ΔV=(−GM2R)−(−GMR)
- Simplifying:
ΔV=−GM2R+GMR=GMR−GM2R=GM2R
- Thus:
ΔV=−V2
- Change in potential energy: ΔU=−U2
- Change in potential: ΔV=−V2
Topper's Solved these Questions
Similar Questions
At a height H from the surface of earth, the total energy of a satellite is equal to the potential energy of a body of equal mass at a height 3R from the surface of the earth (R = radius of the earth). The value of H is
View SolutionAt what height from the surface of the earth, the total energy of satellite is equal to its potential energy at a height 2R from the surface of the earth (R=radius of earth)
View Solution
Knowledge Check
in the previous question, the change in potential energy.
AGMEm2REBGMEm4RECGMEm8REDGMEm16RE
If the potential energy of a spring is V on stretching it by 2cm, then its potential energy when it is stretched by 10cm will be
View SolutionDefine gravitational potential and gravitational potential energy.
View SolutionIf the potential at A is 2000V the potential at B is
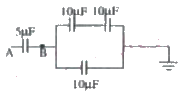
View SolutionA particle is executing SHM with amplitude A. At displacement x=(−A4), force acting on the particle is F, potential energy of the particle is U, velocity of particle is v and kinetic energy is K. Assuming potential energyh to be zero at mean position. At displacement x=A/2
View SolutionDefine potential energy. Derive an expression for the potential energy of a body of mass m, at a height h above the surface of the Earth.
View SolutionKinetic energy of a particle on the surface of earth is E0 and the potential energy is −2E0.
(a) Will the particle escape to infinity ?
(ii) What is the value of potential energy where speed of the particle becomes zero?
View SolutionIn S.H.M., potential energy (U) V/s, time (t) . Graph is
View Solution
