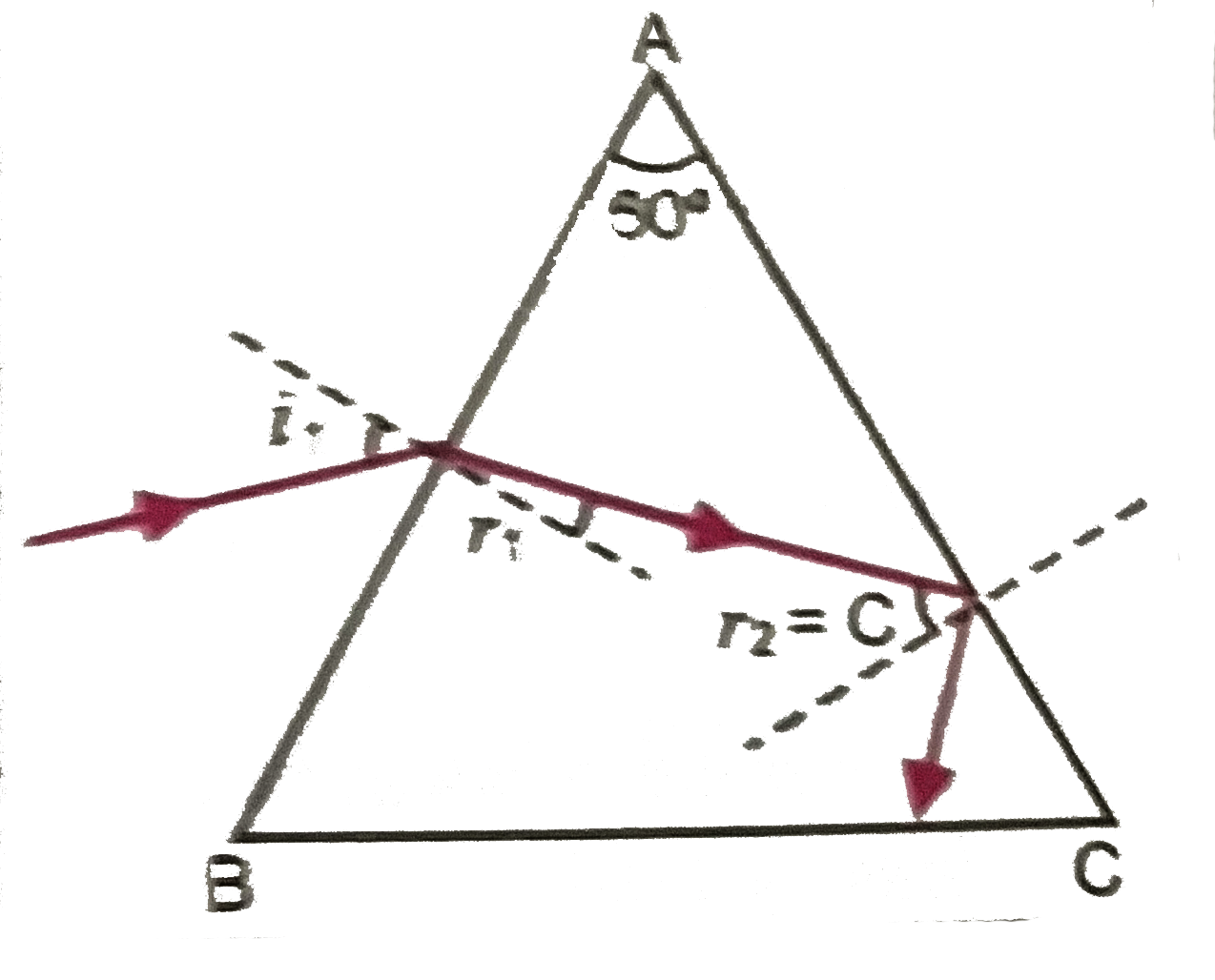
At what angle should a ray of light be incident on the face of a prism of refracting angle , so that it just suffers total internal reflection at the other face ? The refractive index of the prism is .
As and from Fig.
(for total internal reflection at face )
As
As
.
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Higher Thinking Order
Explore 5 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Sample Problem(a)
Explore 5 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:(NCERT)Long Answer
Explore 5 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face ? The refractive index of the material of the prism is 1.524.
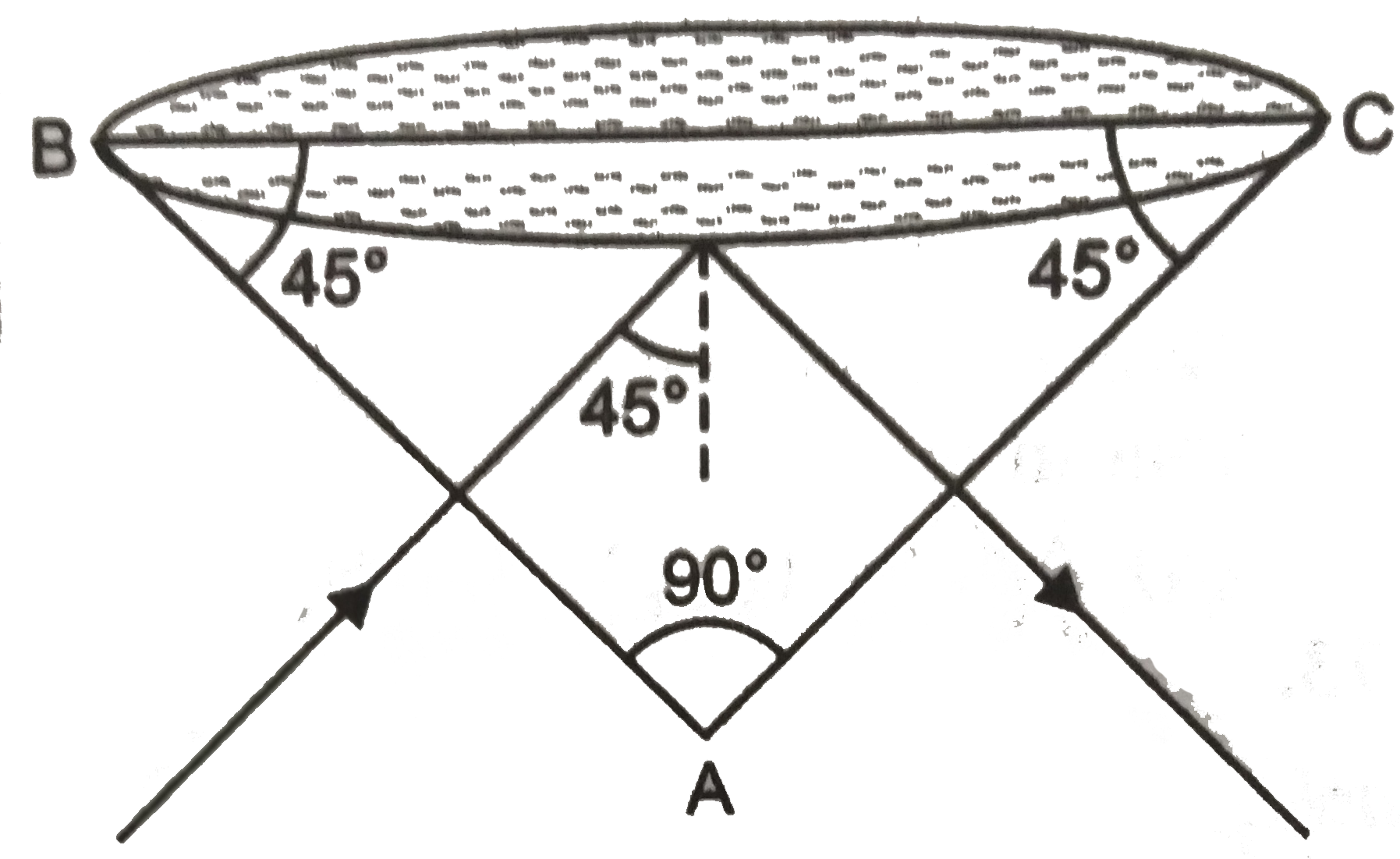
View SolutionA drop of liquid is spread over the hypotenuse of a right angled isosceles prism as shown in Fig. and a ray of light is incident normally on face AB of the prism. If refractive index of liquid is √2, then for total internal reflection to occur, refractive index of material prism should be :
View Solution
Knowledge Check
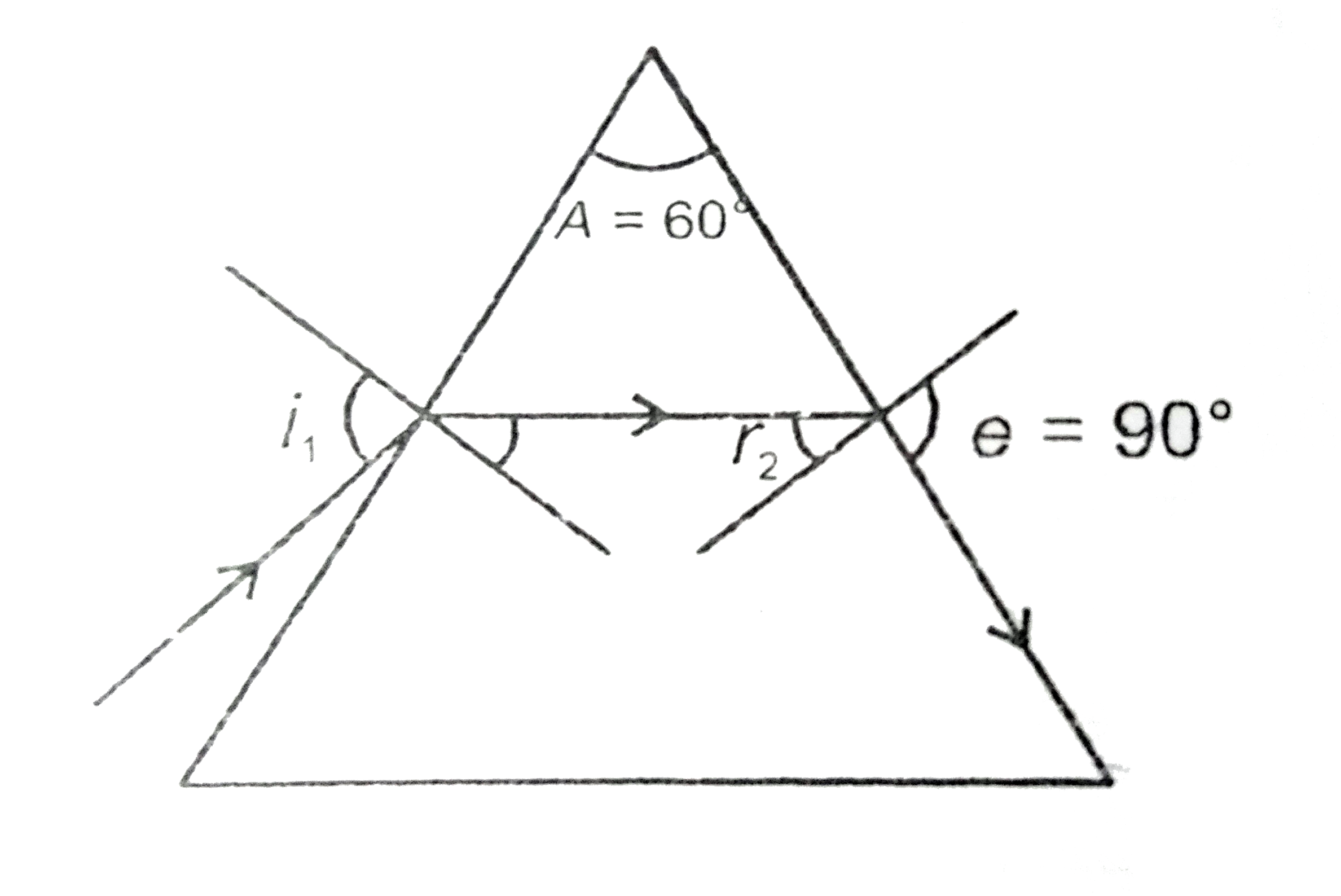
A ray of light is incident at an angle of 60∘ on one face of a prism of angle 30∘. They ray emerges normally from the other face of the prism. The refractive index of the prism material is
A√2B√3C2D3A ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
A1.732B1.414C1.5D1.33A ray of light is incident at 65∘ on one face of a prism of angle of 30∘ and the emergent ray makes 35∘ with the incident ray. The refractive index of the prism is:
A1.812B1.414C1.5D1.33
A ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionCalculate the angle of incidence on the face of a prism of refracting angle 60∘ and of refractive index 1.5, for which the emergent ray just grazes the other face.
View SolutionA ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.
View SolutionA ray of monochromatic light is incident on the refracting face of a prism (angle 75∘0 . It passes through the prism and is incident on the other face at the critical angle. If the refractive index of the prism is √2 , then the angle of incidence on the first of the prism is
View SolutionA ray of monochromatic light is incident on one refracting face of a prism of refracting angle75∘ . It passes through the prism and is incident on the other face at the critical angle If the refracive index of the material of prism is √2, the angle of incidence on the first face o the prism is
View Solution