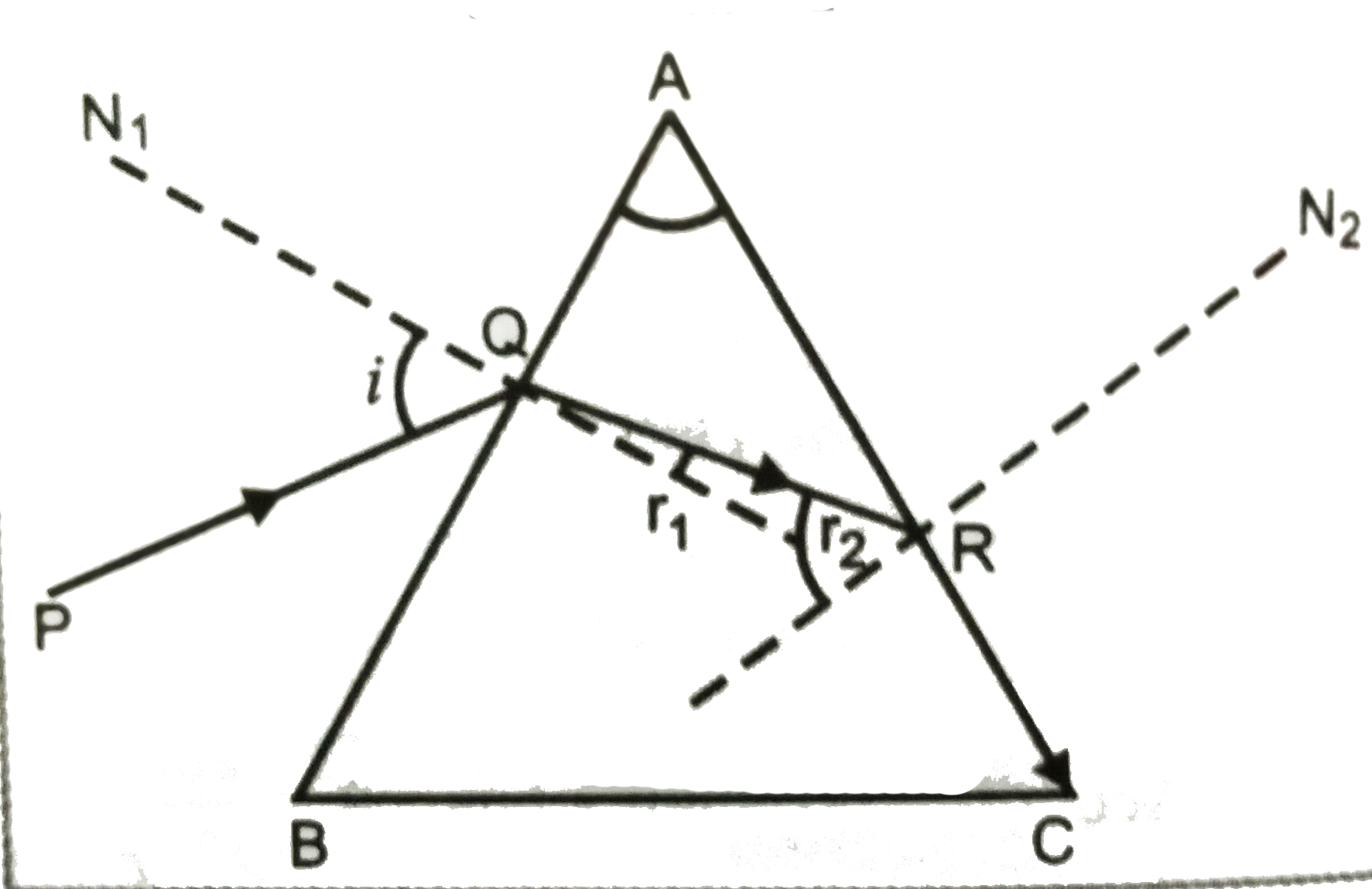
A ray of light is incident on a glass prism of refractive index $μ$ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem of finding the relationship between the angle of incidence (I), the angle of the prism (A), and the critical angle (Ic) when a ray of light is incident on a glass prism and suffers total internal reflection, we can follow these steps:
1. Understand the Geometry of the Prism:
- Let the angle of the prism be $A$ .
- A ray of light is incident on the first face of the prism at an angle of incidence $I$ .
- The ray refracts into the prism and makes an angle $R_{1}$ with the normal at the first surface.
2. Apply Snell's Law at the First Surface:
- According to Snell's law:
$sin I = μ sin R_{1}$
- Here, $μ$ is the refractive index of the prism.
3. Determine the Angles Inside the Prism:
- The angle of refraction $R_{2}$ at the second surface of the prism will be equal to the critical angle $I c$ when total internal reflection occurs.
- The relationship between the angles in the prism can be expressed as:
$R_{1} + R_{2} = A$
- Substituting $R_{2} = I c$ :
$R_{1} + I c = A ⟹ R_{1} = A - I c$
4. Substitute $R_{1}$ in Snell's Law:
- Substitute $R_{1} = A - I c$ into the Snell's law equation:
$sin I = μ sin (A - I c)$
5. Apply Snell's Law at the Second Surface:
- For the second surface, where total internal reflection occurs:
$μ sin I c = sin 90^{\circ}$
- Since $sin 90^{\circ} = 1$ :
$μ = \frac{1}{sin I c}$
6. Substitute $μ$ into the Equation:
- Now substituting $μ$ back into the equation:
$sin I = \frac{1}{sin I c} sin (A - I c)$
7. Final Expression:
- Rearranging gives us:
$sin I = \frac{sin (A - I c)}{sin I c}$
- This can be expressed in terms of the inverse sine function:
$I = {sin}^{- 1} (\frac{sin (A - I c)}{sin I c})$
Final Result:
The relationship between the angle of incidence $I$ , the angle of the prism $A$ , and the critical angle $I c$ is given by:
$I = {sin}^{- 1} (\frac{sin (A - I c)}{sin I c})$

Updated on:7/8/2024