Average acceleration is in the direction of .
Initial velocity
Finial velocity
Change in velocity
Final velocity if initial velocity is zero.
The correct Answer is:C, D
To solve the question regarding the direction of average acceleration, we can follow these steps:
1. Understand the Concept of Average Acceleration:
Average acceleration is defined as the change in velocity over a time interval. Mathematically, it can be expressed as:
Average Acceleration(aavg)=ΔvΔt
where Δv is the change in velocity and Δt is the time interval.
2. Identify the Change in Velocity:
The change in velocity (Δv) is calculated as:
Δv=vf−vi
where vf is the final velocity and vi is the initial velocity.
3. Determine the Direction of Average Acceleration:
Since average acceleration is derived from the change in velocity, its direction is the same as the direction of the change in velocity. Therefore, the average acceleration points in the direction of Δv.
4. Evaluate the Options:
Given the options:
- A) Initial velocity
- B) Final velocity
- C) Change in velocity
- D) Velocity
We can conclude:
- The direction of average acceleration is the same as the direction of the change in velocity (Δv).
- Thus, option C (Change in velocity) is correct.
- Additionally, since average acceleration is also related to final velocity when initial velocity is zero, option B (Final velocity) can also be considered correct in this specific case.
5. Final Conclusion:
Therefore, the average acceleration is in the direction of the change in velocity (option C) and, under the condition of initial velocity being zero, also in the direction of final velocity (option B).
Average acceleration is defined as the change in velocity over a time interval. Mathematically, it can be expressed as:
Average Acceleration(aavg)=ΔvΔt
where Δv is the change in velocity and Δt is the time interval.
The change in velocity (Δv) is calculated as:
Δv=vf−vi
where vf is the final velocity and vi is the initial velocity.
Since average acceleration is derived from the change in velocity, its direction is the same as the direction of the change in velocity. Therefore, the average acceleration points in the direction of Δv.
Given the options:
- A) Initial velocity
- B) Final velocity
- C) Change in velocity
- D) Velocity
- The direction of average acceleration is the same as the direction of the change in velocity (Δv).
- Thus, option C (Change in velocity) is correct.
- Additionally, since average acceleration is also related to final velocity when initial velocity is zero, option B (Final velocity) can also be considered correct in this specific case.
Therefore, the average acceleration is in the direction of the change in velocity (option C) and, under the condition of initial velocity being zero, also in the direction of final velocity (option B).
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Assertion-reasoning
5 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Linked Comprehension
30 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical cancept
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
Which of the quantity, velocity or acceleration determines the direction of motion ?
View SolutionFor any particle moving with some velocity (→v) & acceleration (→a), tangential acceleration & normal acceleration are defined as follows.
Tangential acceleration - The component of acceleration in the direction of velocity.
Normal acceleration - The component of acceleration in the direction perpendicular to velocity.
If at a given instant, velocity & acceleration of a particle are given by .
→c=4ˆi+3ˆj
→a=10ˆi+15ˆj+20ˆk
Find the tangential acceleration of the particle at the given instant :-
View SolutionFor any particle moving with some velocity (→v) & acceleration (→a), tangential acceleration & normal acceleration are defined as follows.
Tangential acceleration - The component of acceleration in the direction of velocity.
Normal acceleration - The component of acceleration in the direction perpendicular to velocity.
If at a given instant, velocity & acceleration of a particle are given by .
→c=4ˆi+3ˆj
→a=10ˆi+15ˆj+20ˆk
Find the normal acceleration of the particles at the given instant :-
View SolutionThe v-t graph for a particle moving along x-axis is shown in the figure, find
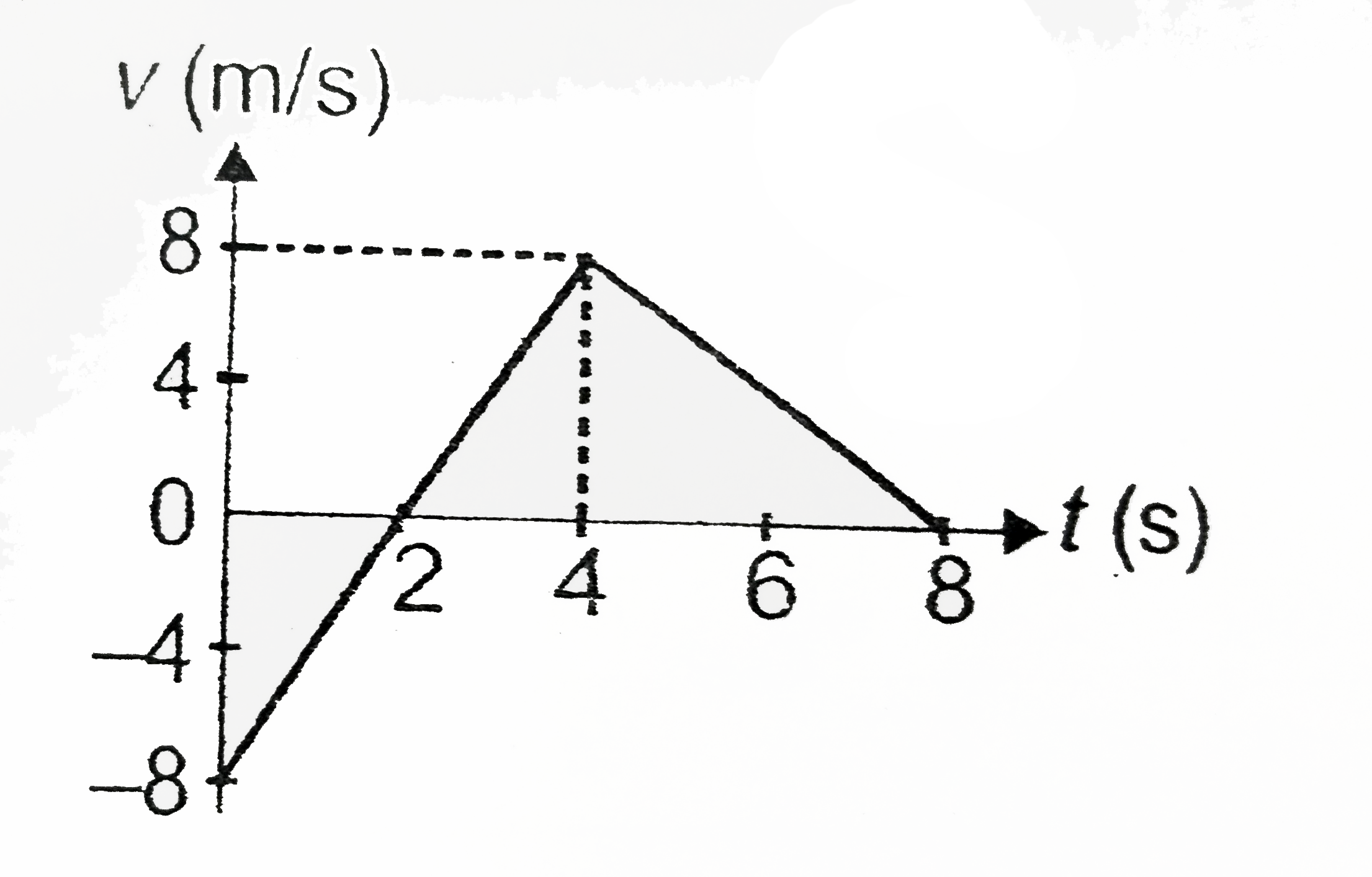
(a) Average velocity in the interval 0 to 8 s.
(b) Average speed in the interval 0 to 8 s.
(c) Average acceleration in the interval 0 to 4 s.
(d) Instantaneous acceleration at t = 2.5 s.
View SolutionA uniform circular motion is an accelerated motion. Explain it. State whether the acceleration is uniform or variable? Name the force responsible to cause this acceleration. What is the direction of force at any instant? Draw a diagram in support of your answer.
View SolutionA particle is moving along a circle of radius R with a uniform speed v. At t=0 , the particle is moving along the east. Find the average acceleration (magnitude and direction) in 1/4th revolution.
View SolutionThe average acceleration in one time period in a simple harmonic motion is
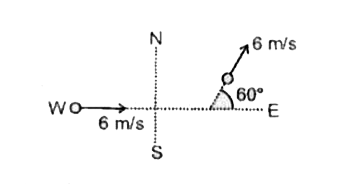
View SolutionA particle is moving eastwards with a speed of 6 m/s. After 6 s, the particle is found to be moving with same speed in a direction 60∘ north of east. The magnitude of average acceleration in this interval of time is
View SolutionFive persons A, B, C, D & E are pulling a cart of mass 100kg on a smooth surface and cart is moving with acceleration 3m/s2 in east direction. When person A' stops pulling, it moves with acceleration 1m/s2in the west direction. When person 'B' stops pulling, it moves with accele-ration 24m/s2 in the north direction. The magnitude of acceleration of the cart when only A & B pull the cart keeping their directions same as the old direction is
View SolutionThe velocity-time graph of an object is given below. Calculate the average acceleration of the object in the time interval of 4 s to 6 s.

View Solution
