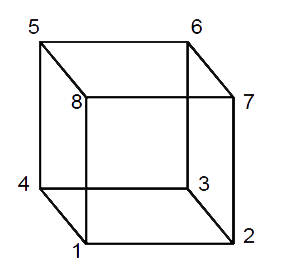
Battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω (Fig. 3.23). Determine the equivalent resistance of the network and the current along each edge of the cube.
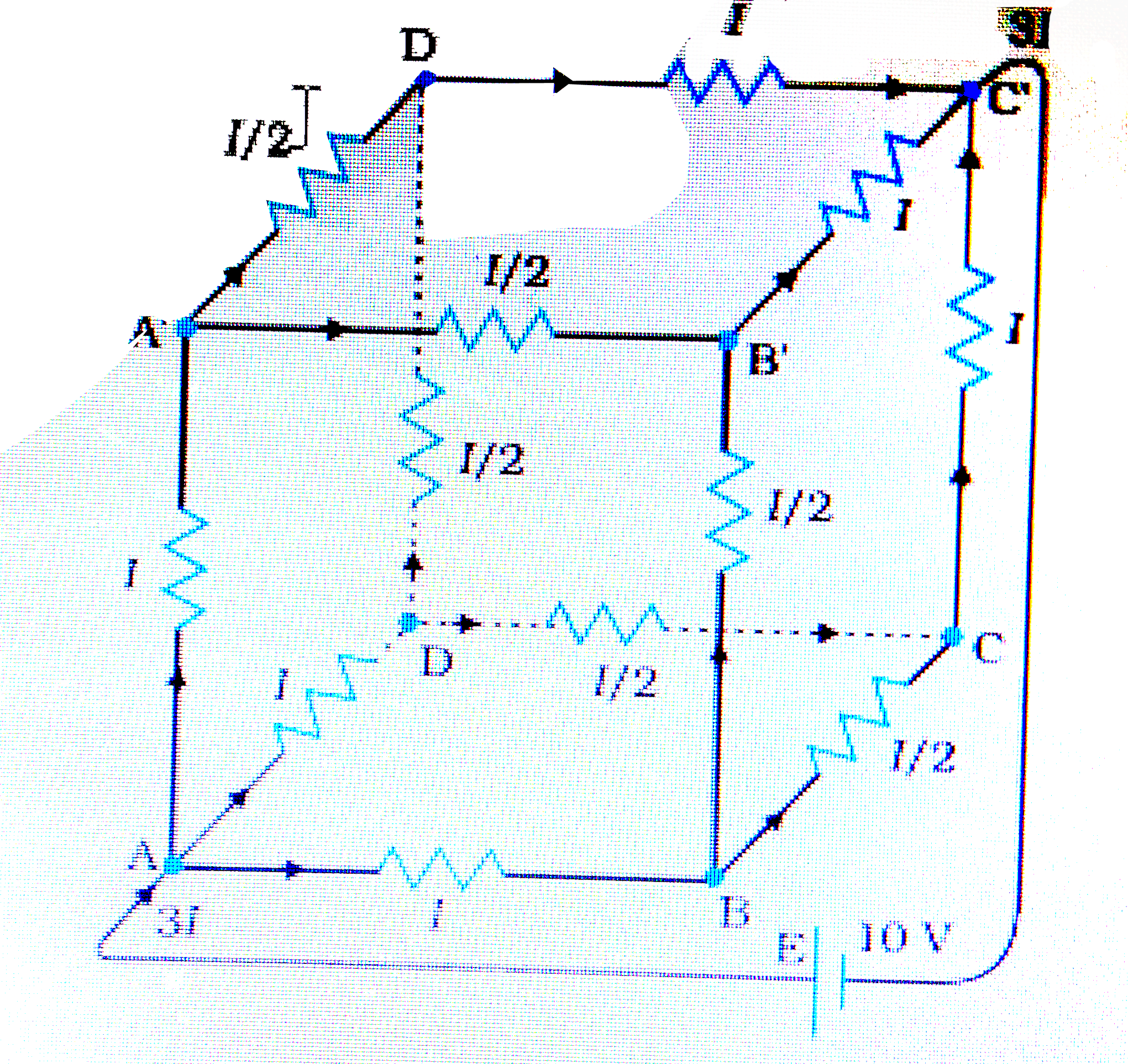

Let 6I be the current through the cell. At junction A, this current will get divided into three equal parts (due to symmetry). Current through AD will again get divided into two equal parts at junction D. So DC and DE will have current I. Similarly, BC, BG, HE and HG will also have current I flowing through them. The current through DC and BC will meet and add at junction C and thus, current 2I will flow through the path CF. Similarly, current 2I will flow through EF and GF. These three currents will reunite at F again and will add to 6I again. Applying Kirchhoff.s loop rule to AHGFA, we get −2IR−IR−2IR+ε=0
⇒2IR+IR+2IR−ε=0
∴5IR=ε
The equivalent resistance of the network is
⇒R.=Total emfTotal current=ε6I=5IR6I=56R
Given, R=1Ω
∴R.=56Ω
∴ Total current in the network is
6I=εR.=105=12A
⇒I=126=2Λ
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE PROBLEMS
71 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
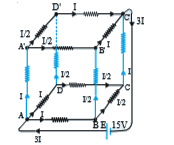
View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.

View Solution
Knowledge Check
Three resistors each of 4Ω are connected together to form a network. The equivalent resistance of the network cannot be
A1.33ΩB3.0ΩC6.0ΩD12.0ΩTwelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
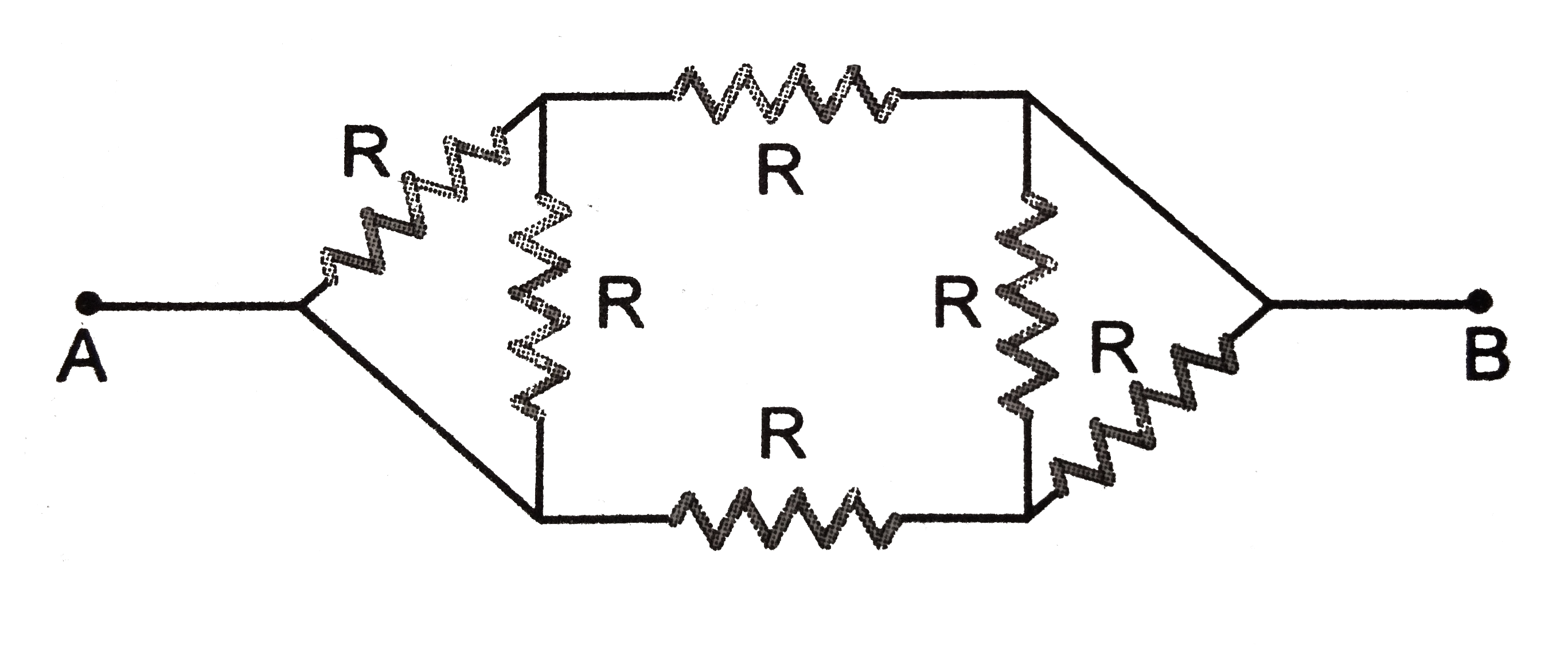
A56Ω and 12AB65Ω and 12 AC56Ω 4AD65Ω and 4AThe figure shows a network of resistor each having value 12Ω. Find the equivalent resistance between points A and B.
 A9ΩB125ΩC8ΩD113Ω
A9ΩB125ΩC8ΩD113Ω
The terminals of a battery of emf 3 V and internal resistance 2.5Ω are joined to the diagonally opposite corners of a cubical skeleton frame of 12 wires, each of resistance 3Ω. Find the current in the battery.
View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

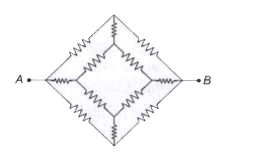
View SolutionWhat is the equivalent resistance between A and B of network .Each resistance is of RΩ
View SolutionA battery of e.m.f 10V and internal resistance 3Omega is connected to a resistor.If the current in the circuit is 0.5A,then the resistance of the resistor is
View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
When current enters at 1 and leaves at 3
View Solution
