Block B of mass rests on block A, with mass which in turn is on a horizontal tabletop (as shown in figure) .The coefficient of kinetic friction between block A and the tabletop is and the coefficient of static friction between block A and blockB is A light string attached block A passes over a frictionless, massless pulley and block C is suspeneded from the other end of the string. What is the largest mass (in kg) that block C can have so that block A and B still slide together when the system is relaced from rest?

The correct Answer is:
Since the seurface beneth the block B is smooth , therefore the block B will move to right
Since A remain stationary relative to B therefore acceleration of A and B are identical, let it be a, hence acceleration of block C will also be equal to a but vertically downward
Since A has the tendency to slip to the right over the surface of B hence friction on A will act leftward and on block B rightward
Maximum possible value of mass of block C will correspond to limiting friction between block B and C hence FBD will be as shown in figure

For vertical equilibrium of A
or
For horizontal forces on A
For horizontal forces on B
For force on or if mass of blocks C equal to or will slip over the surface at B it mean acceleration of A will be greater than that of B let acceleration of block A be a then acceleration of c will also be equal to a but vertically downward and lot acceleration of block B be b (rightward)
Now FBD will be as shown in figure
For block A
...(i)
For block B
for block C ...(ii)
from Eqs (i) and (ii)
Block A will separate from B other B after through over it .hence considering rightward motion of A retative to B inital velocity
Acceleration
or
Using
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.3
27 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A block of mass m slides in right angled incliine through as shown in the figure . If the coefficient of kinetic friction between the block and the through is μk , find the acceleration of the block .

View SolutionA block B of mass 5kg is placed on a slab A of mass 20kg which lies on a frictionless surface as shown in the figure. The coefficient of static friction between the block and the slab is 0.4 and that of kinetic friction is 0.2. If a force F = 25N acts on B, the acceleration of the slab will be:

View Solution
Knowledge Check
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
A10NB5NC2.5ND20N
Block B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block is
View SolutionUsing the diagram from the previous example, assurme that m=2 kg, M= 10 kg, and the coefficient of kinetic friction between the small block and the tabletop is 0.5. What is the acceleration of the blocks ?
View SolutionA block A of mass 2kg rests on another block B of mass 8kg which rests on a horizontal floor. The coefficient of friction between A and B is 0.2 while that between B and floor is 0.5.When a horizontal floor F of 25N is applied on the block B the force of friction between A and B is
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
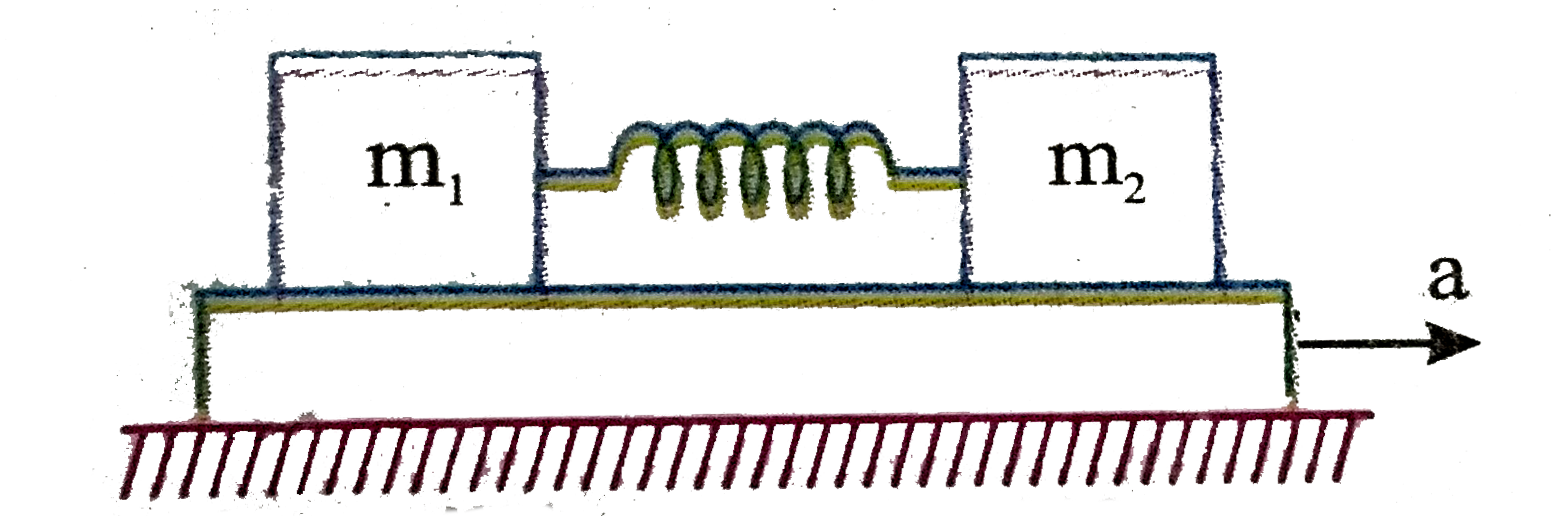
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When

View Solution
