Calculate the change in magnetic field induction at the centre of a current carrying loop of radius R, if the radius of coil is reduced to half and current through it changes from I to 2I .
The correct Answer is:3μ0I2R
To solve the problem, we need to calculate the change in magnetic field induction at the center of a current-carrying loop when the radius is reduced to half and the current is doubled.
1. Understand the Formula for Magnetic Field:
The magnetic field B at the center of a circular loop carrying current I and having radius R is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space.
2. Calculate Initial Magnetic Field B1:
For the initial loop with radius R and current I:
B1=μ0I2R
3. Calculate New Magnetic Field B2:
For the new loop with radius R2 and current 2I:
B2=μ0(2I)2(R2)=μ0(2I)R=2μ0IR
4. Calculate the Change in Magnetic Field ΔB:
The change in magnetic field is given by:
ΔB=B2−B1
Substituting the values we calculated:
ΔB=2μ0IR−μ0I2R
To combine these fractions, we need a common denominator:
ΔB=2μ0IR−μ0I2R=4μ0I2R−μ0I2R=3μ0I2R
5. Final Result:
The change in magnetic field induction at the center of the loop is:
ΔB=3μ0I2R
The magnetic field B at the center of a circular loop carrying current I and having radius R is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space.
For the initial loop with radius R and current I:
B1=μ0I2R
For the new loop with radius R2 and current 2I:
B2=μ0(2I)2(R2)=μ0(2I)R=2μ0IR
The change in magnetic field is given by:
ΔB=B2−B1
Substituting the values we calculated:
ΔB=2μ0IR−μ0I2R
To combine these fractions, we need a common denominator:
ΔB=2μ0IR−μ0I2R=4μ0I2R−μ0I2R=3μ0I2R
The change in magnetic field induction at the center of the loop is:
ΔB=3μ0I2R
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Conceptual Questions
29 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Tough & Tricky (PROBLEMS )
15 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - CHAPTER PRACTICE TEST
13 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
Knowledge Check
The magnetic induction at the centre of a current carrying circular of coil radius r, is
ADirectly proportional to rBInversely proportional rCDirectly proportional to rDInversely proportional to rWhat will be magnetic field at centre of current carrying circular loop of radius R?
Aμ0I4πRBμ0I2πRCμ0I2RDzeroRatio of magnetic field at the centre of a current carrying coil of radius R and at a distance of 3R on its axis is
A10√10B20√10C2√10D√10
Magnetic field induction at the centre O of a square loop of side a carrying current I as shown in figure.
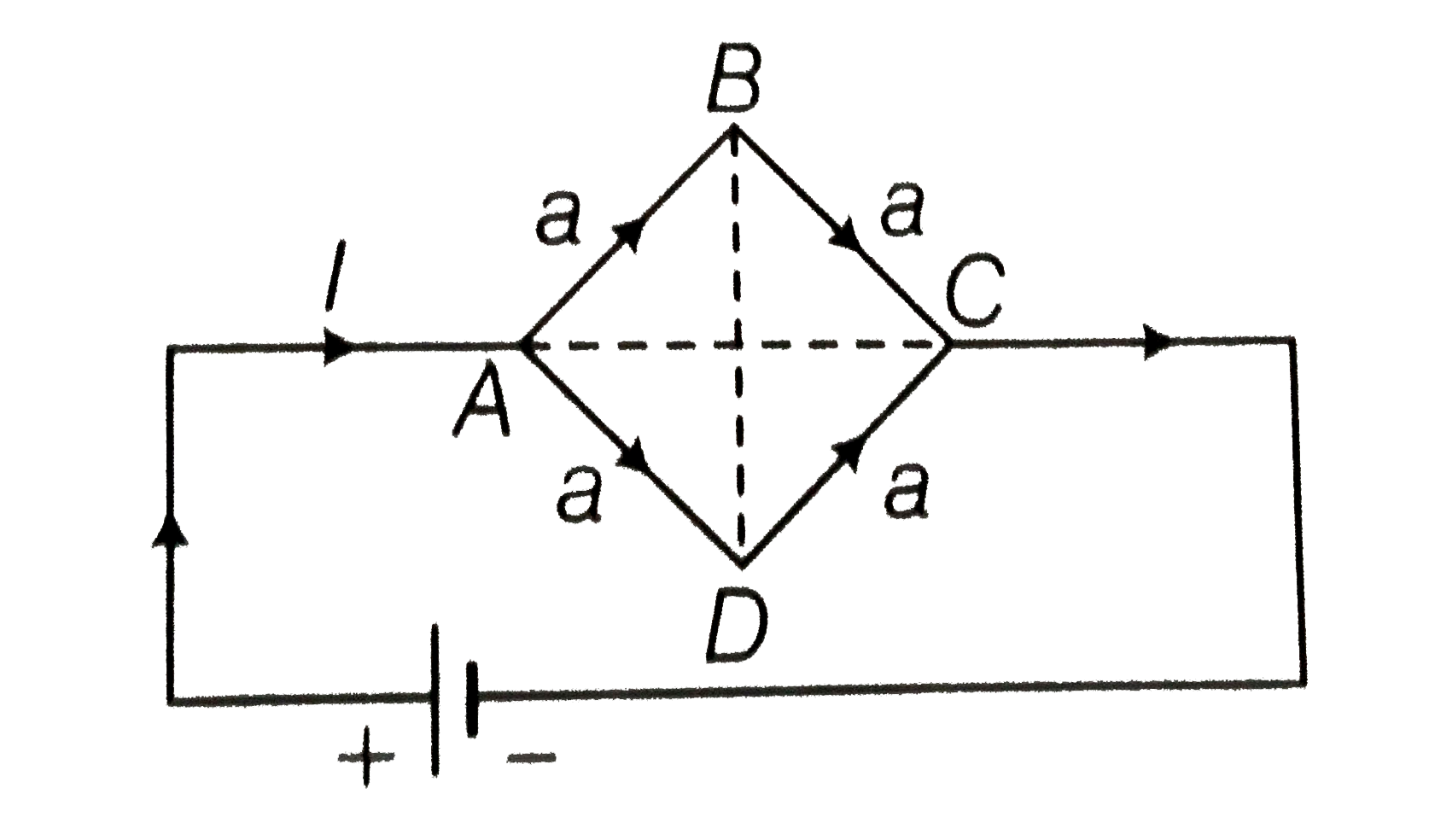
View SolutionWhat happens to the magnetic field at the centre of a circular current carrying coil if we double the radius of the coil keeping the current unchanged?
View SolutionMagnetic field intensity H at the centre of a circular loop of radius r carrying current I e.m.u. is
View SolutionMagnetic field induction at the centre of a square loop of side 'a' carrying current I as shown in figure is
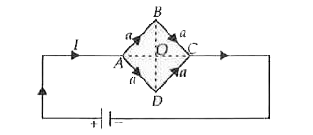
View SolutionThe magnetic field at the centre of current carrying coil is B0. If its radius is reduced to half keeping current the same, then magnetic field at its centre become
View Solution

