Magnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
√3μ0iπl
6μ0iπl
2μ0iπl
3μ0iπl
To find the magnetic field at the center of a regular hexagon current-carrying loop of side length L and current I, we can follow these steps:
Step 1: Understand the Geometry of the Hexagon
A regular hexagon has 6 equal sides and is symmetric. Each interior angle of a regular hexagon is 120∘. The center of the hexagon is equidistant from all vertices.
Step 2: Calculate the Magnetic Field Due to One Side
The magnetic field B at a distance D from a straight current-carrying wire is given by the formula:
B=μ0I4πD
where μ0 is the permeability of free space, I is the current, and D is the perpendicular distance from the wire to the point where the magnetic field is being calculated.
Step 3: Determine the Perpendicular Distance
For a regular hexagon, the distance D from the center to the midpoint of any side can be calculated using trigonometry. The distance from the center to a vertex is L√3 (height of the triangle formed by the hexagon). The angle subtended at the center by each side is 60∘, so:
D=L2√3
Step 4: Calculate the Magnetic Field Contribution from One Side
Using the distance D in the magnetic field formula:
Bone side=μ0I4π(L2√3)=μ0I⋅2√34πL=μ0I√32πL
Step 5: Total Magnetic Field from All Sides
Since there are 6 sides in the hexagon and the contribution of the magnetic field from each side adds up (due to symmetry and the same direction of current), the total magnetic field B at the center is:
B=6⋅Bone side=6⋅μ0I√32πL=3μ0I√3πL
Step 6: Final Expression for Magnetic Field
Thus, the magnetic field at the center of the regular hexagon current-carrying loop is:
B=√3μ0IπL
A regular hexagon has 6 equal sides and is symmetric. Each interior angle of a regular hexagon is 120∘. The center of the hexagon is equidistant from all vertices.
The magnetic field B at a distance D from a straight current-carrying wire is given by the formula:
B=μ0I4πD
where μ0 is the permeability of free space, I is the current, and D is the perpendicular distance from the wire to the point where the magnetic field is being calculated.
For a regular hexagon, the distance D from the center to the midpoint of any side can be calculated using trigonometry. The distance from the center to a vertex is L√3 (height of the triangle formed by the hexagon). The angle subtended at the center by each side is 60∘, so:
D=L2√3
Using the distance D in the magnetic field formula:
Bone side=μ0I4π(L2√3)=μ0I⋅2√34πL=μ0I√32πL
Since there are 6 sides in the hexagon and the contribution of the magnetic field from each side adds up (due to symmetry and the same direction of current), the total magnetic field B at the center is:
B=6⋅Bone side=6⋅μ0I√32πL=3μ0I√3πL
Thus, the magnetic field at the center of the regular hexagon current-carrying loop is:
B=√3μ0IπL
Topper's Solved these Questions
Similar Questions
Knowledge Check
The magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
A9μ0i4πLB3√3μ0i4πLC2√3μ0iπLD3μ0i4πLThe magnetic field at the centre of current carrying coil is
Aμ0ni2rBμ02πnirCμ0ni4rDμ0niThe ratio of magnetic field and magnetic moment at the centre of a current carrying circular loop is x. When both the current and radius is doubled the ratio will be
Ax8Bx4Cx2D2x
Find the experssion for the magnetic field at the centre O of a coil bent in the form of a square of side 2a, carrying current I, figure.
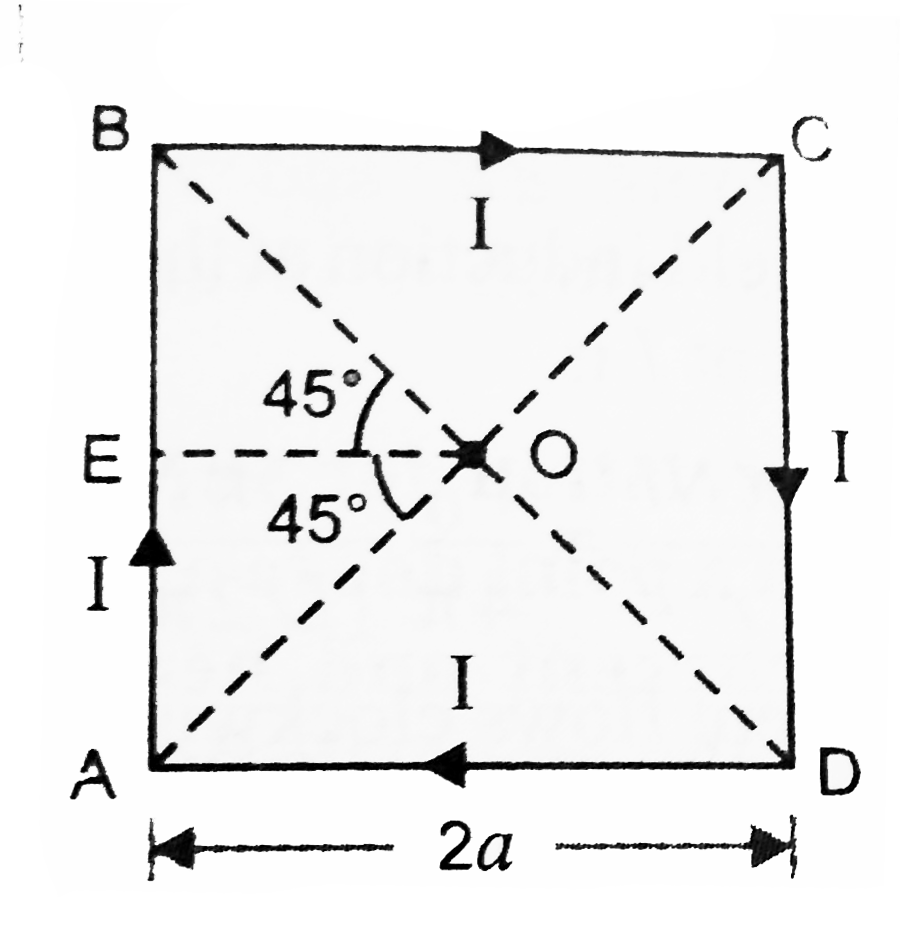
View SolutionMagnetic field induction at the centre O of a square loop of side a carrying current I as shown in figure.
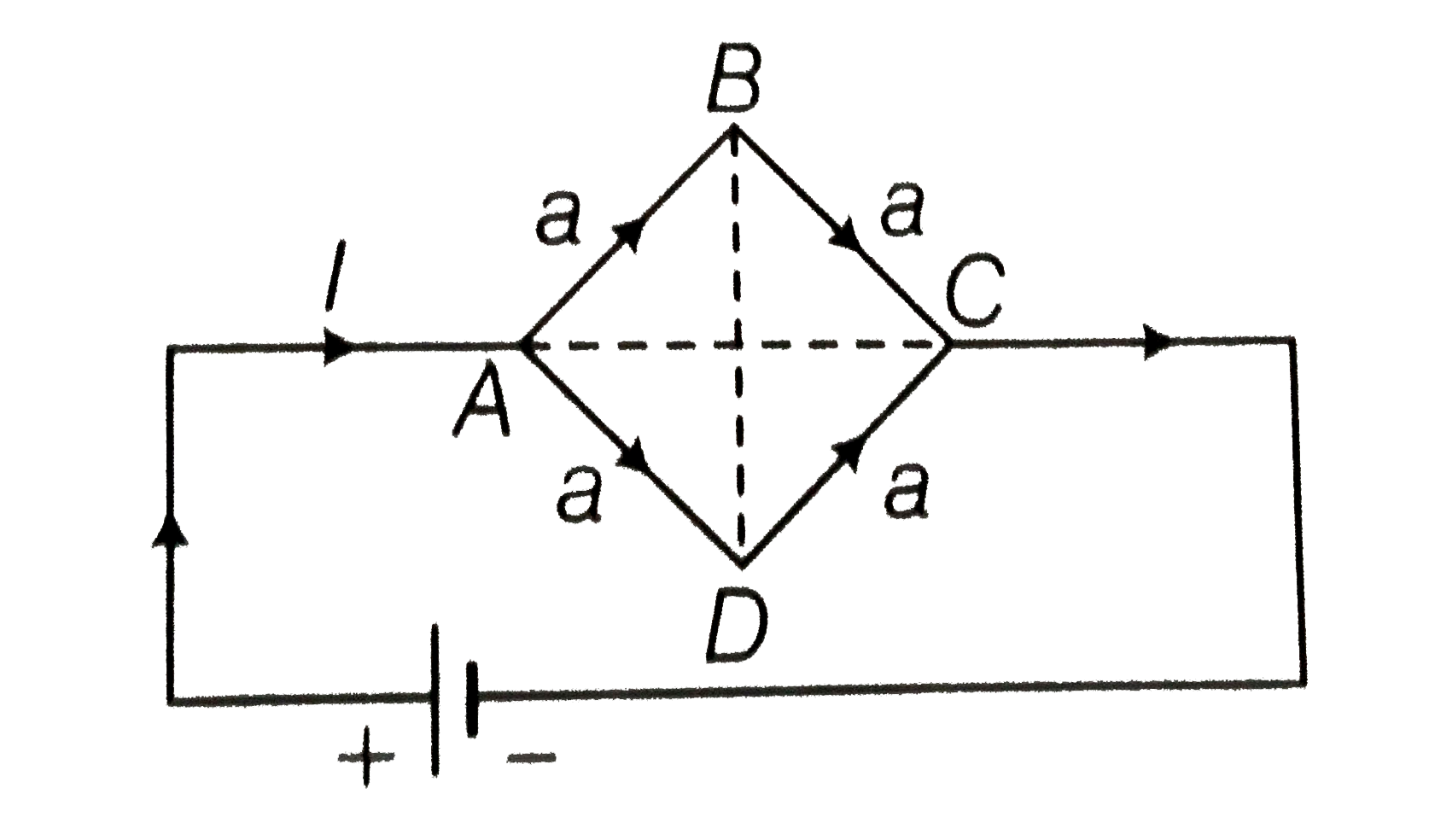
View SolutionThe magnetic field at the centre of a current carrying circular loop is B. If the radius of the loop is doubled, keeping the current same, the magnetic field at the centre of the loop would be :
View SolutionThe magnetic field at the centre of a current carrying circular loop is B. If the radius of the loop is doubled, keeping the current same, the magnetic field at the centre of the loop would be :
View SolutionMagnetic field induction at the centre of a square loop of side 'a' carrying current I as shown in figure is
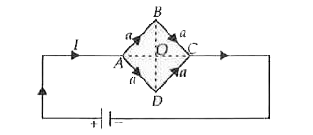
View Solution
