Calculate, the gravitational field at point O due to three massesm1,m2andm3 whose positions are given by the following figure. If the masses m1andm2 are equal what is the change in gravitational field at the point O?Solution in Tamil
Gravitational field due to m1 at a point .O . is →E1=Gm1a2ˆi
Gravitational field due to .m1 at a point .O. is →E2=−Gm2a2ˆi
(Negative sign indicates field acting along negative x direction )
Gravitational field due to m3 at a point . O . is →E3=Gm3a2ˆj
→E=→E1+→E2+→E3=Gm1a2ˆi−Gm2a2ˆi+Gm3a2ˆj
→E=Ga2[(m1−m2)ˆi+m3ˆj]
If the masses m1=m2, then
→E=Gm3a2ˆj

Topper's Solved these Questions
- GRAVITATIONBOOK - FULL MARKSCHAPTER - GRAVITATIONEXERCISE - ADDITIONAL QUESTIONS SOLVED (I. Choose the correct answer from the following)
43 Videos
- GRAVITATIONBOOK - FULL MARKSCHAPTER - GRAVITATIONEXERCISE - ADDITIONAL QUESTIONS SOLVED (2 Marks Questions)
8 Videos
- GRAVITATIONBOOK - FULL MARKSCHAPTER - GRAVITATIONEXERCISE - TEXTUAL EVALUATION SOLVED (IV. Conceptual Questions)
6 Videos
- EXAMINATION QUESTION PAPER MARCH 2019BOOK - FULL MARKSCHAPTER - EXAMINATION QUESTION PAPER MARCH 2019EXERCISE - PART-IV
10 Videos
- HEAT AND THERMODYNAMICSBOOK - FULL MARKSCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - ADDITIONAL QUESTIONS SOLVED (Numerical Problems)
16 Videos
Similar Questions
According to Kepler's planet move in
View SolutionDistinguish between the terms gravitation and gravity.
View SolutionThe work done by Sun on Earth in one year will be:
View SolutionThe force F acting on a body moving in a circular path depends on mass of the body (m) velocity(v) and radius (r) of the circular path. Obtain the expression for the force by dimensional analysis method (k=1)
View SolutionThe length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. The natural length of the wire is:
View SolutionTwo bodies of masses M_(1) and M_(2) , are placed at a distance R apart. Then at the position where the gravitational field due to them is zero, the gravitational potential is
View SolutionTwo bodies of masses m1 and m2 are placed at a distance r apart. Show that the position where the gravitational field due to them is zero, the potential is given by
−G(m1+m2+2√m1+m2)/r
View SolutionTwo bodies of masses M1 and M2 are kept separeated by a distance d. The potential at the point where the gravitational field produced by them is zero, is :-
View SolutionThe gravitational force between two point masses m1 and m2 at separation r is given by F=km1m2r2
The constant k doesn't
View SolutionThe gravitional force between two point masses m_(1) and m_(2) at separation r is given by F=k (m_(1)m_(2))/r^(2) The constant k
View SolutionTwo bodies of masses m1andm2 ar placed at a distance r apart. Shows that the position where the gravitational field due to them is zer, the potential is given by
V=−Gr[m1+m2+2√m1m2]
View SolutionConsider three concentric shells of masses M1,M2andM3 having radii a,b and c respectively are situated as shown in

Gravitational field at a point located at Q and P is
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
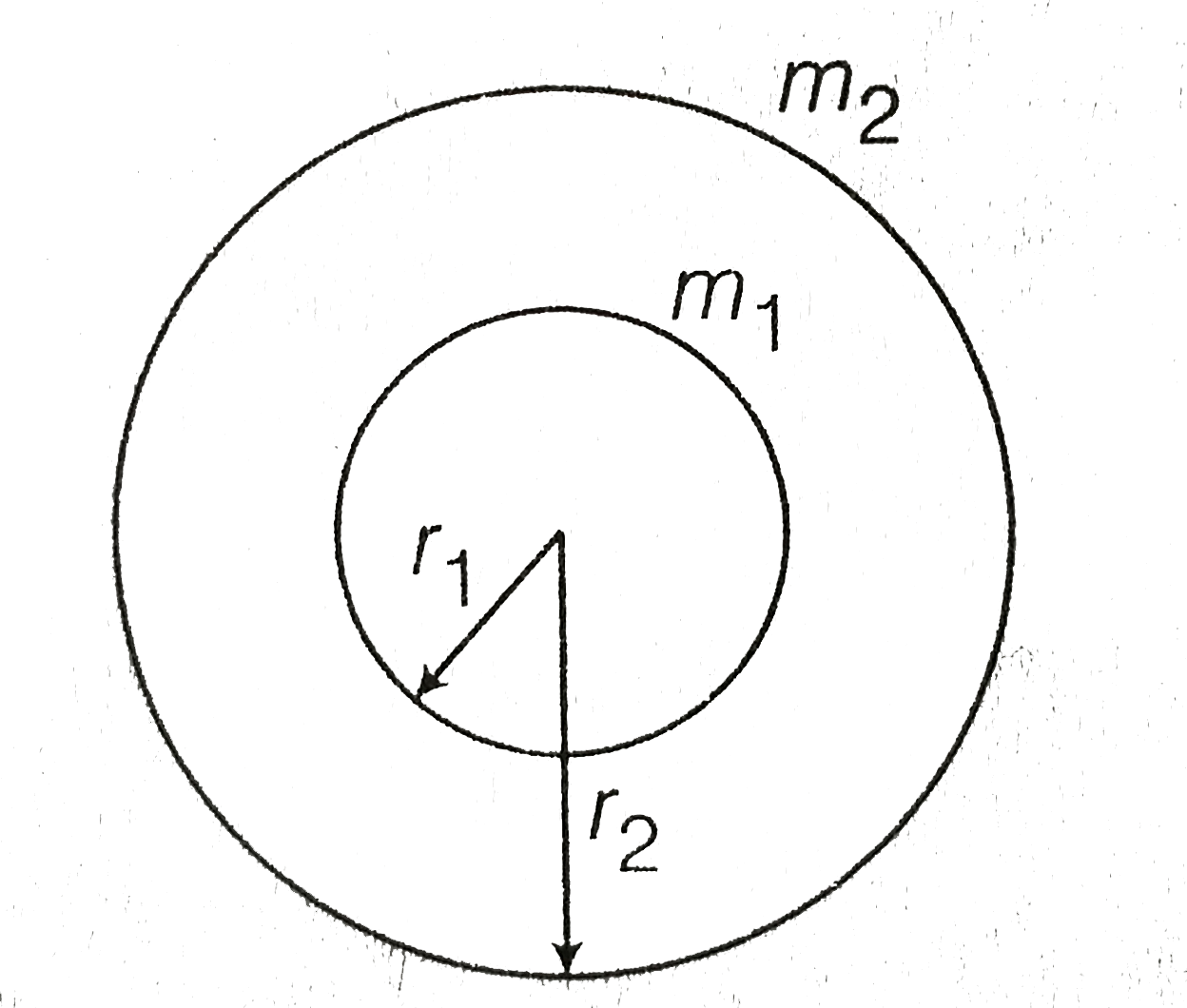
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View SolutionF is the gravitational force between two point masses m1 and m2 , separated by a distance d. A point mass 2m1 is then brought near m1. What is the total force on m2 ?
View SolutionM1 और M2 द्रव्यमान के दो पिंड d दूरी पर स्थित हैं । सिद्ध कीजिए कि उस स्थिति में , जहाँ पर उनके कारण गुरुत्वीय क्षेत्र शून्य है , विभव निम्न समीकरण द्वारा दिया जाता है -
V=−Gd(M1+M2+2√M1M2).
View Solution
