Consider three concentric shells of masses M1,M2andM3 having radii a,b and c respectively are situated as shown in

Gravitational field at a point located at Q and P is
G(M1+M2)y2,G(M1+M2)y2
G(M1+M2+M3)Y2,G(M1+M2)x2
G(M1+M2+M3)a2,GM1a2
G(M1+M2+M3)C2,GM2b2
The correct Answer is:B
Gravitational field at an external point due to spherical shell of mass M is (GMr2) while at an internal point is zero
(i) Point Q is external to shell, M1,M2andM3 So, field at Q will be
EQ=GM1y2+GM2y2+GM3y2=Gy2(M1+M2+M3)
(ii) Field at P will be
Fp=GM1x2+GM2x2+0=Gx2(M1+M2).
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.410videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.520videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.220videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE11videos
KINEMATICS
Similar Questions
Two concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is
 View Solution
View SolutionTwo concentric shells of masses M1 and M2 are concentric as shown. Calculate the gravitational force on m due to M1 at points P,Q and R.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two concentric shells of masses M1 and M2 are having radii r1 and r2. Which of the following is the correct expression for the gravitational field on a mass m?
 AF=G(M1+M2)r2, for r<r1BF=G(M1+M2)(r2), for r<r2CF=GM2r2, for r1<r<r2DF=GM1r2, for r1<r<r2
AF=G(M1+M2)r2, for r<r1BF=G(M1+M2)(r2), for r<r2CF=GM2r2, for r1<r<r2DF=GM1r2, for r1<r<r2 - Question 2 - Select One
Two concentric shells have masses M and m and their radii are R and r, respectively, where R>r. What is the gravitational potential at their common centre?
A−GMRB−GMrC−G[MR−mr]D−G[MR+mr] - Question 3 - Select One
The figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is
 AG(M1+M2)a2BGM1a2+GM2R22CGM1a2Dzero
AG(M1+M2)a2BGM1a2+GM2R22CGM1a2Dzero
Find the potential V at P in the gravitational field of fixed point mass M.
View SolutionTwo concentric spherical shells A and B of radii R and 2R and mases 4M, and M, respectively are placed in space as shown in Fig. The gravitational potential at P at a distance r(R<r<2R)from the centre of shells is
 View Solution
View SolutionThree concentric spherical shells A, B and C having uniformly distributed total charges +Q, -2Q and +Q respectively are placed as shown. The potential at the centre will be -
 View Solution
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
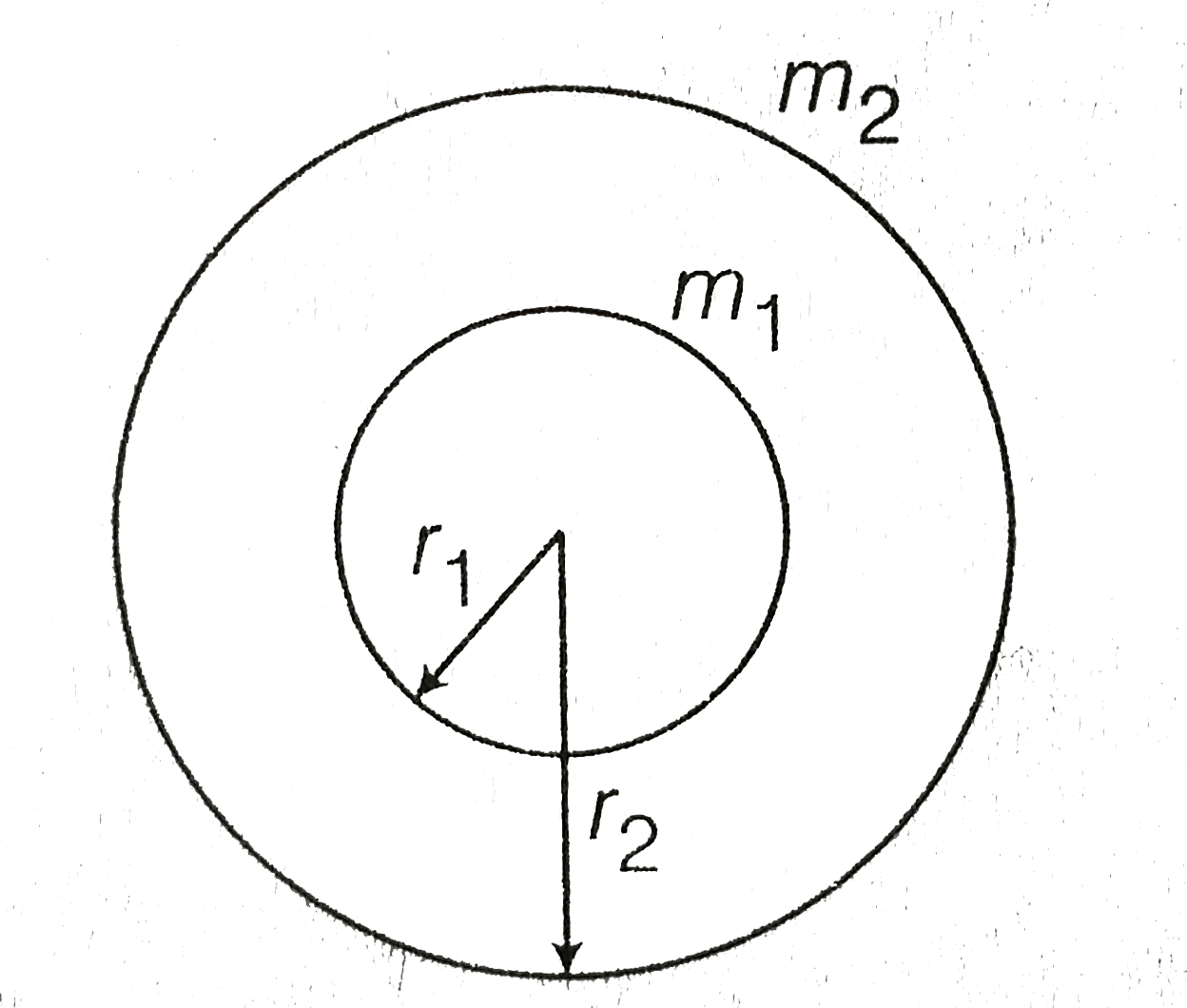
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).View SolutionTwo bodies of masses M1 and M2 are kept separeated by a distance d. The potential at the point where the gravitational field produced by them is zero, is :-
View Solution

