Calculate the maximum possible value of mass m0 of block C upto which blockA will remain stationary relative to B .If the length of block B is equal to l=50cm and mass of block C is m3=2m0 then calculate the time l when block A will topple from block B .If the system is released from rest

The correct Answer is:1kg0.6s
Since the seurface beneth the block B is smooth , therefore the block B will move to right
Since A remain stationary relative to B therefore acceleration of A and B are identical, let it be a, hence acceleration of block C will also be equal to a but vertically downward
Since A has the tendency to slip to the right over the surface of B hence friction on A will act leftward and on block B rightward
Maximum possible value of mass mA of block C will correspond to limiting friction between block B and C hence FBD will be as shown in figure

For vertical equilibrium of AN1=m1g
or N1=10N
For horizontal forces on A
T−μN=m1a⇒T=(a+203)
For horizontal forces on B μN1=m2a
a=52ms−2⇒T=a+203=253
For force on C,m0g−T=m0.a or m0=1kg if mass of blocks C equal to m3=2m2g or 2kg,A will slip over the surface at B it mean acceleration of A will be greater than that of B let acceleration of block A be a then acceleration of c will also be equal to a but vertically downward and lot acceleration of block B be b (rightward)
Now FBD will be as shown in figure
For block A
N1=m2gorN1=10N
T=μN1=m1a⇒f=(a+203)...(i)
For block B μN1=m2borb=5/3ms−2
for block C m3g−T=m3g...(ii)
from Eqs (i) and (ii)
T=1009Nanda=409ms−2
Block A will separate from B other B after through l=510cm over it .hence considering rightward motion of A retative to B inital velocity a=0
Acceleration =a−259ms−2
s=50cm or 0.50mt=?
Using v=a+12at2⇒r=0.6s
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.3
27 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Given the setup shown in Fig Block A,B and C have masses mA=M and mB=mC=m. The strings are assumed maseless and unstreichable, and the pulleys frictionless .There is no friction between block B and the support table, but there is friction between blocks B and C, denoted by a given coefficient μ

a . In terms the given find (i) the acceleration of block A and B
b. Suppose the system is released from rest with block C near the right end of block B as shown in the above figure. If the the length L of block B is given, what is the speed of block C as it reached the left end of block B ? Tear the size of C as small
c. If the mass of block A is less then some critical value, the blocks will not accelerate when released from rest. Write down as expression for that critical mass.
View SolutionThe system shown in figure starts from rest, and each block moves with a constant acceleration. If the relative acceleration of block C with respect to block B is 6m/s2 upward and the relative acceleration of block D with respect to block C after 3s from starts.
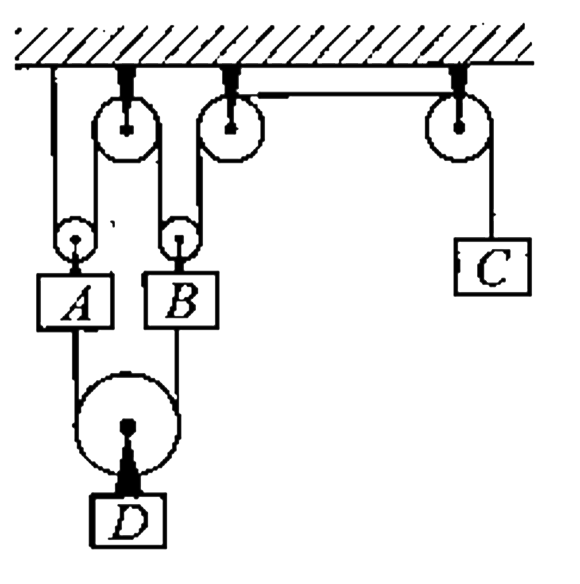
View Solution
Knowledge Check
In the system shown all the surfaces are frictionless while pulley and string are massless. The mass of block A is 2m and that of block B is m. The acceleration of block B immediately after system is released from rest is
 Ag/2BgCg/3DNone of these
Ag/2BgCg/3DNone of these
In the arrangement shown in the figure mAmB=23 and the ratio of density of block B and the liquid is 2:1 The system is released from rest. ThenAblock B will oscillate but not simple harmonicallyBblock B will oscillate simple harmonicallyCthe system will remain in equilibariumDNone of the aboveIn the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
 .AThe maximum extension of the spring is 4mgk.BThe speed of A when extension in spring is 2mgk is 2g√2m3k.CThe acceleration of block B when the extension in the spring is maximum, is 23gDTension in the thread for extension of 2mgk in spring is mg
.AThe maximum extension of the spring is 4mgk.BThe speed of A when extension in spring is 2mgk is 2g√2m3k.CThe acceleration of block B when the extension in the spring is maximum, is 23gDTension in the thread for extension of 2mgk in spring is mg
A block with mass m1 is placed on an inclined plane with slope angle α and is connected to a second hunging block with mass m2 by a cord passing over a small . Friction less pulley as shown in fig 7.247 . The coefficient of static friction is μ2 and the coefficient of kinetic friction is μs

a. Find the mass m2 for which block m1 moves up plane at constant speed once it is set in motion
b. Find the mass m2 for which block m1 moves down the plane at constant speed once it is set in motion
c.For what range of m2 will the blocks remain at rest if they are released from rest?
View SolutionThree blocks A, B, & C are arranged as shown. Pulley and strings are ideal. All surfaces are frictionless. If block C is observed moving down along the incline at 1m/s2. Find mass of block B, tension in string and accelerations of A. B as the system is released from rest.
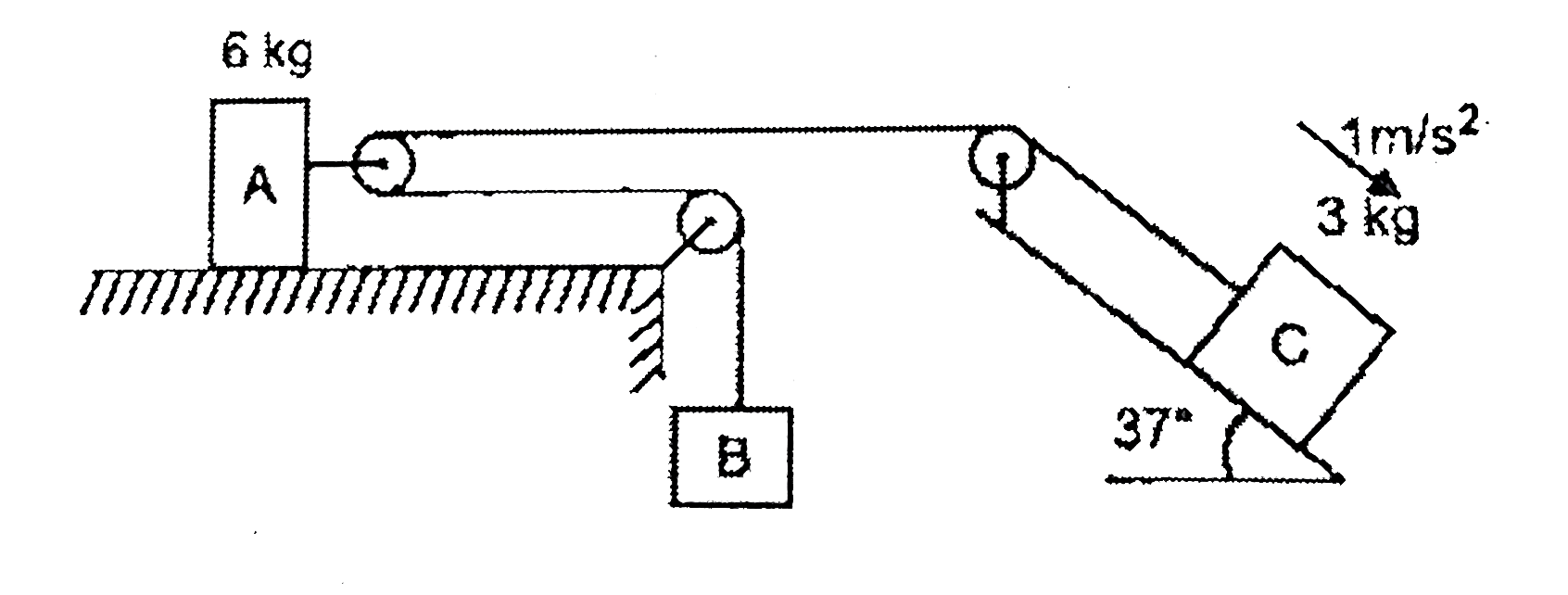
View SolutionA horizontal force F acts on the block of mass m and the block remains stationary, thr value of friction force is.

View SolutionThe coefficient of friction between the block A of mass m & block B of mass 2m is μ. There is no friction between block B & the inclined plane. If the system of blocks A & B is released from rest & there is no slipping between A & B then :
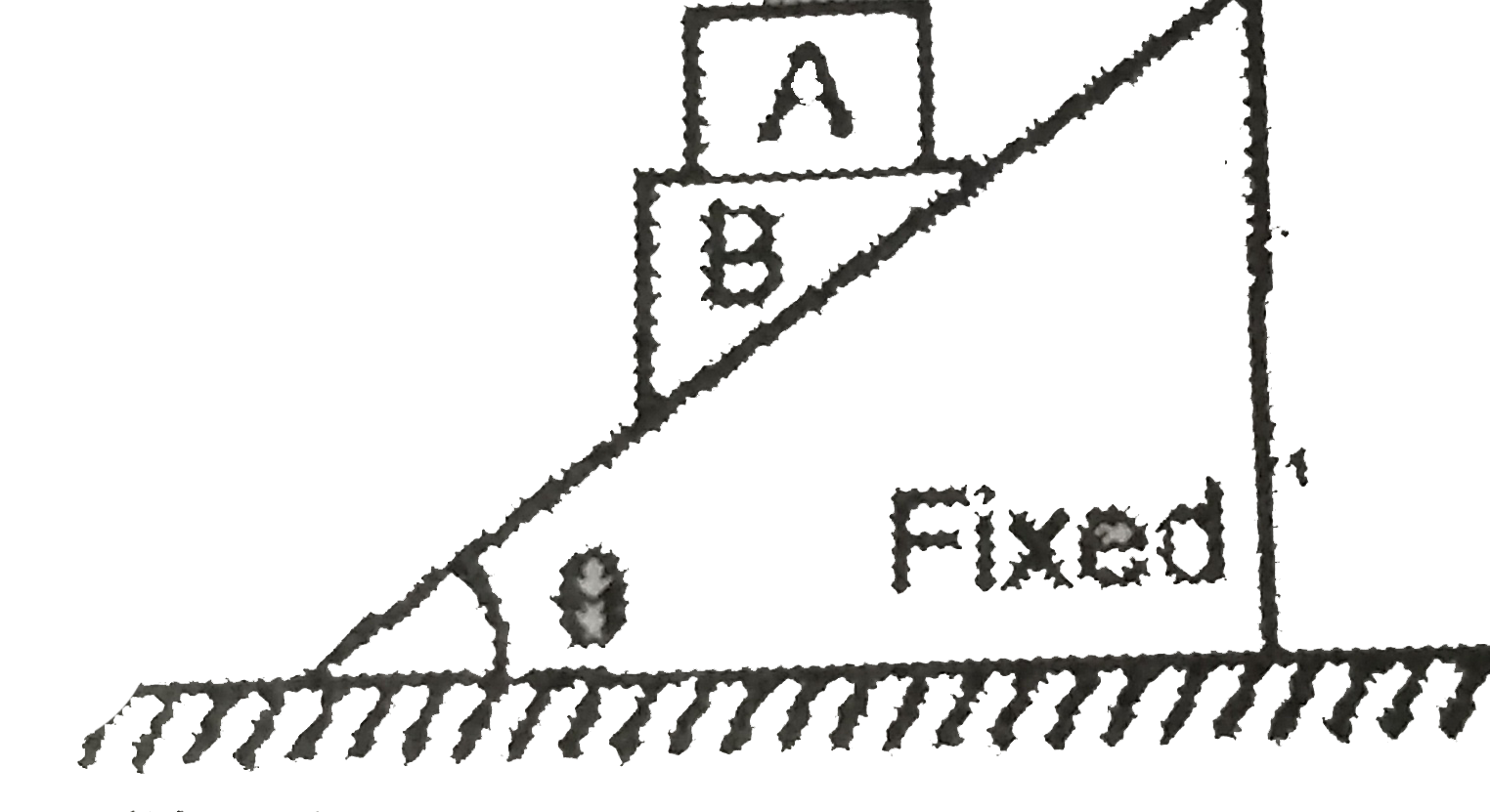
View SolutionThree blocks A,B, and C are suspended as shown in fig. Mass of each of blocks A and B is m. If the system is in equilibrium, and mass of C is M then

View Solution
