Calculate the mutual inductance of a long straight wire and a rectangular frame with sides a and b. The frame and the wire lie in the same plan, with the side b being closent to the wire, separated by a distance l from it and oriented parallel to it.
Here, B=μ0I2πr at a distance r from the wire. The flux through the frame is obtained as,
Φ12=∫a+llμ0I2πrbdr=μ0b2πI In (1+al)
Thus, L12=Φ12I=μ0b2πIn(1+al)

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field36videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics69videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Find the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.
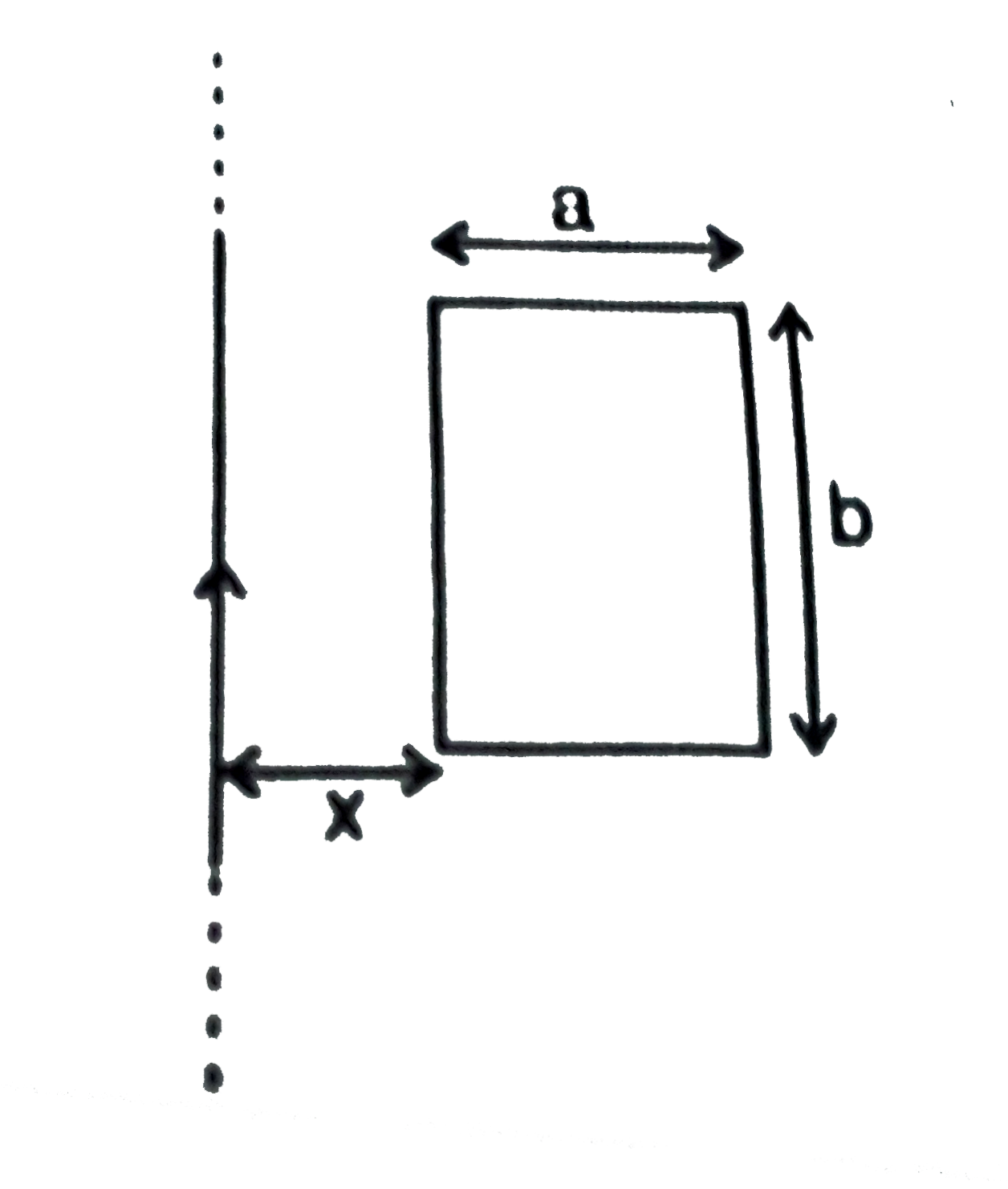 View Solution
View SolutionA square frame carrying a current I is located in the same plane as a long straight wire carrying a current I0 The frame side has a length a. The axis of the frame passing through the midpoints of the opposite sides is parallel to the wire and is separated from it by the distance which is η times greater than the side of the frame. Find
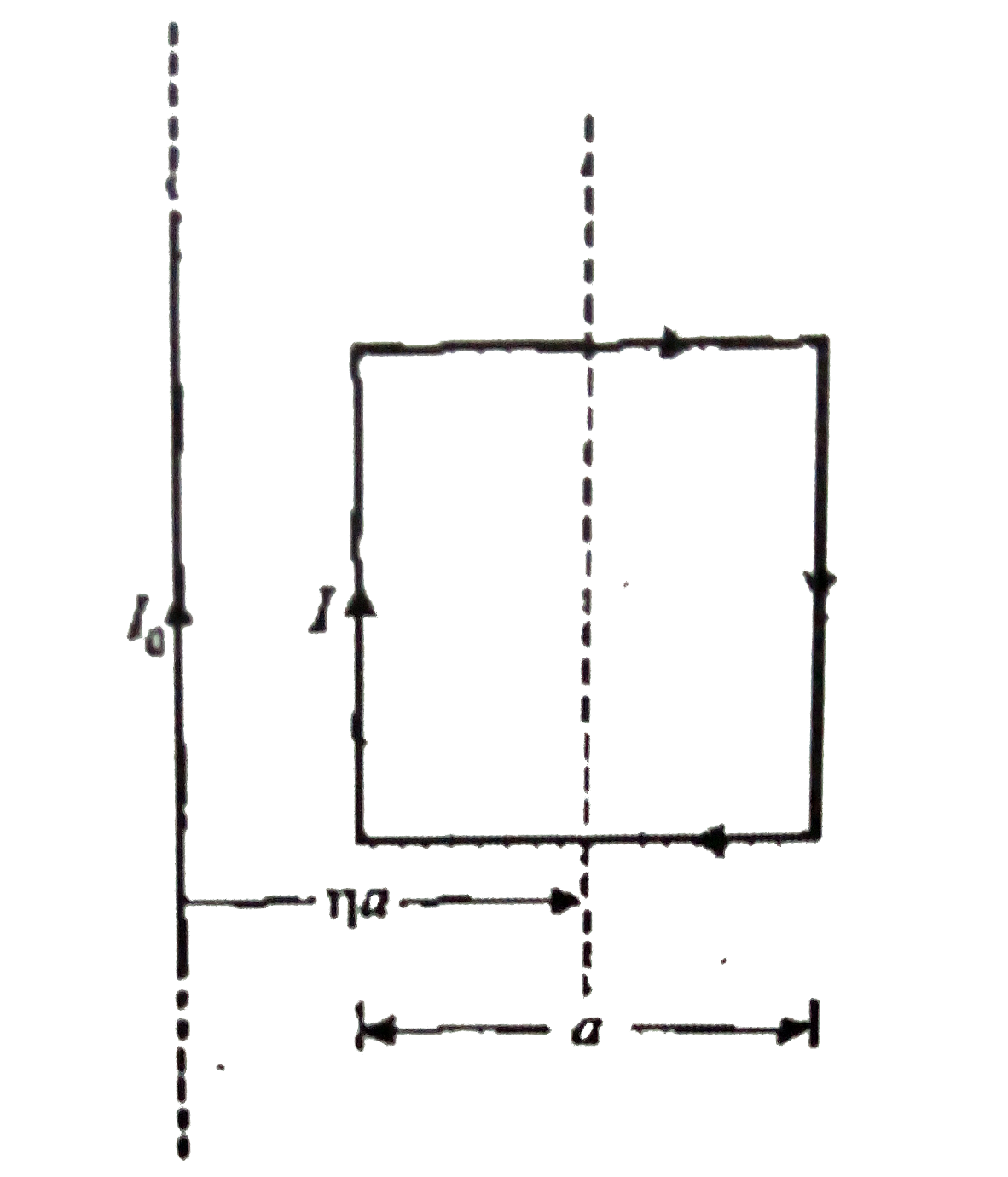
(a) Force acting on the frame
(b) The mechanical work to be performed in order to turn the frame through 180∘ about its axis, with the currents maintained constant.View Solution
Knowledge Check
- Question 1 - Select One
The mutual inductance between the rectangular loop and the long straight wire as shown in figure is M.
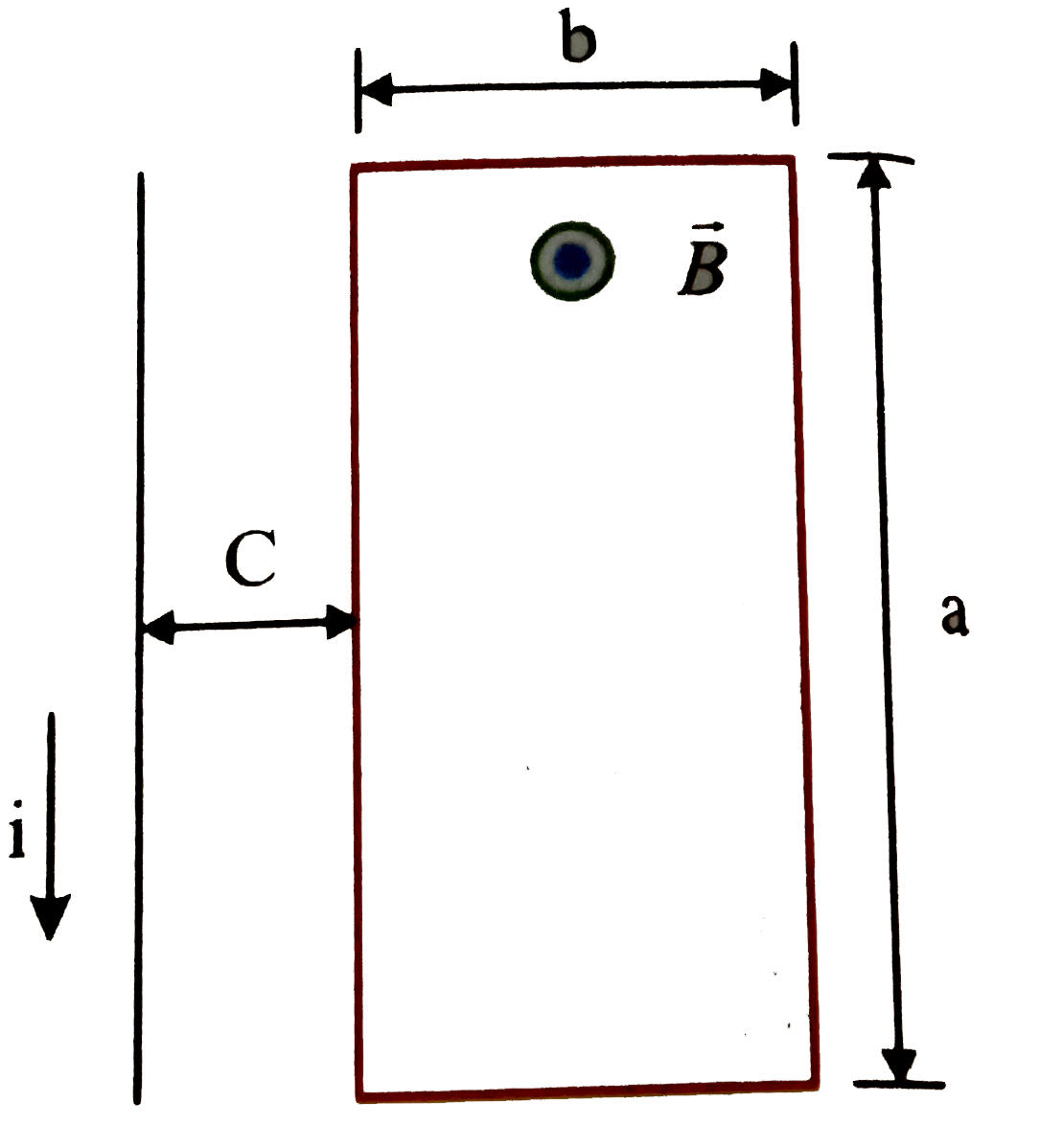 AM= zeroBM=μ0a2πln(1+cb)CM=μ0a2πln(a+bb)DM=μ0a2πln(1+bb)
AM= zeroBM=μ0a2πln(1+cb)CM=μ0a2πln(a+bb)DM=μ0a2πln(1+bb) - Question 2 - Select One
The mutual inductance between the rectangular loop and the long straight wire as shown in figure is M.
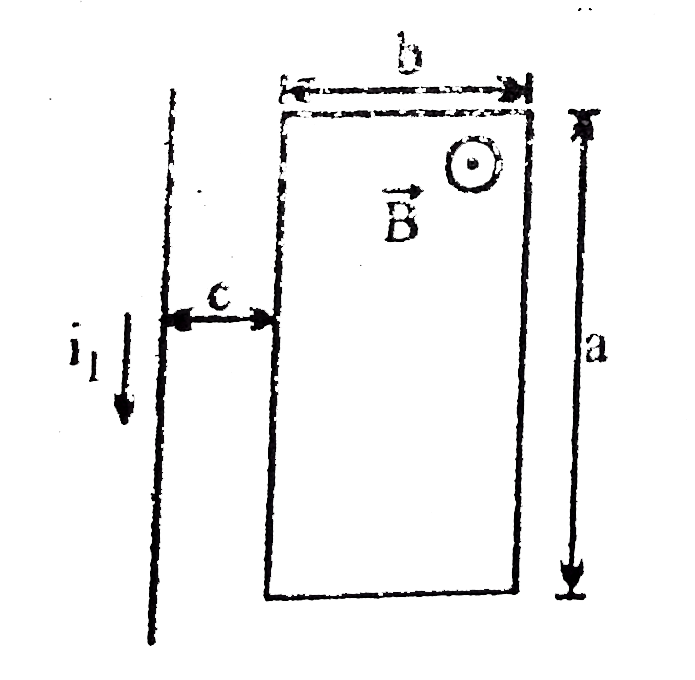 AM=ZeroBM=μ0a2πIn(1+cb)CM=μ0b2πIn(a+cb)DM=μ0a2πIn(1+bc)
AM=ZeroBM=μ0a2πIn(1+cb)CM=μ0b2πIn(a+cb)DM=μ0a2πIn(1+bc) - Question 3 - Select One
If same current I passing through two parallel wires separated by a distance b, then force per unit length will he
Aμ04π2I2bBμ0I4πbCμ0I24πb2Dμ0I24πb
A square frame carrying a current I=0.90A is located in the same plane as a long straight wire carrying a current I0=5A, The frame side has a length a=8cm. The axis of the frame passing through the mid-point of the opposite sides is parrallel to the wire and is separated form it by a distance h=15 times greater tahn the side of the frame.
Find:
(a) ampere force acting on the frame.
(b) The machanical work to be performed in order to turn the frmae through 180∘ about its axis, with the current maintained constant.
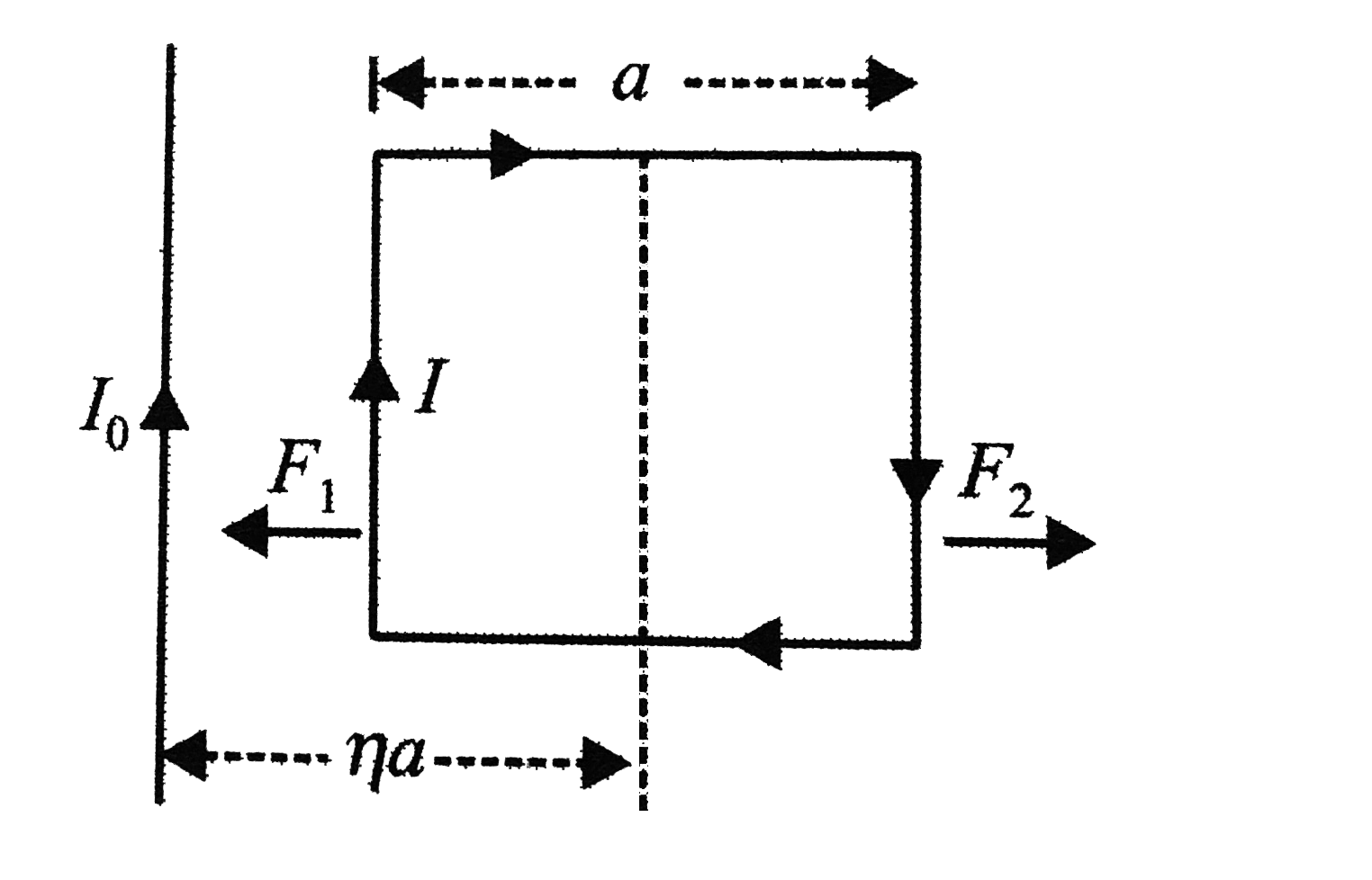 View Solution
View SolutionA square frame carrying a current I=0.9A is located in the same plane as a long straght wire carrying a current, I0=5.0A. The frame side has a length a=8.0cm. The axis of the frame passing thorugh the midpoints of opposite sides is parallel to the wire and is separated from it by the distance which is η=1.5 times greater than the side of the frame. FInd:
(a) Ampere force acting on the frame,
(b) the mechnical work to be performed in order to turn the frame throguh 180∘ about its axis, with the currents maintained constant.View SolutionA square frame carrying a current I=0.9A is located in the same plane as a long straght wire carrying a current, I0=5.0A. The frame side has a length a=8.0cm. The axis of the frame passing thorugh the midpoints of opposite sides is parallel to the wire and is separated from it by the distance which is η=1.5 times greater than the side of the frame. FInd:
(a) Ampere force acting on the frame,
(b) the mechnical work to be performed in order to turn the frame throguh 180∘ about its axis, with the currents maintained constant.View SolutionThe magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
View Solution

