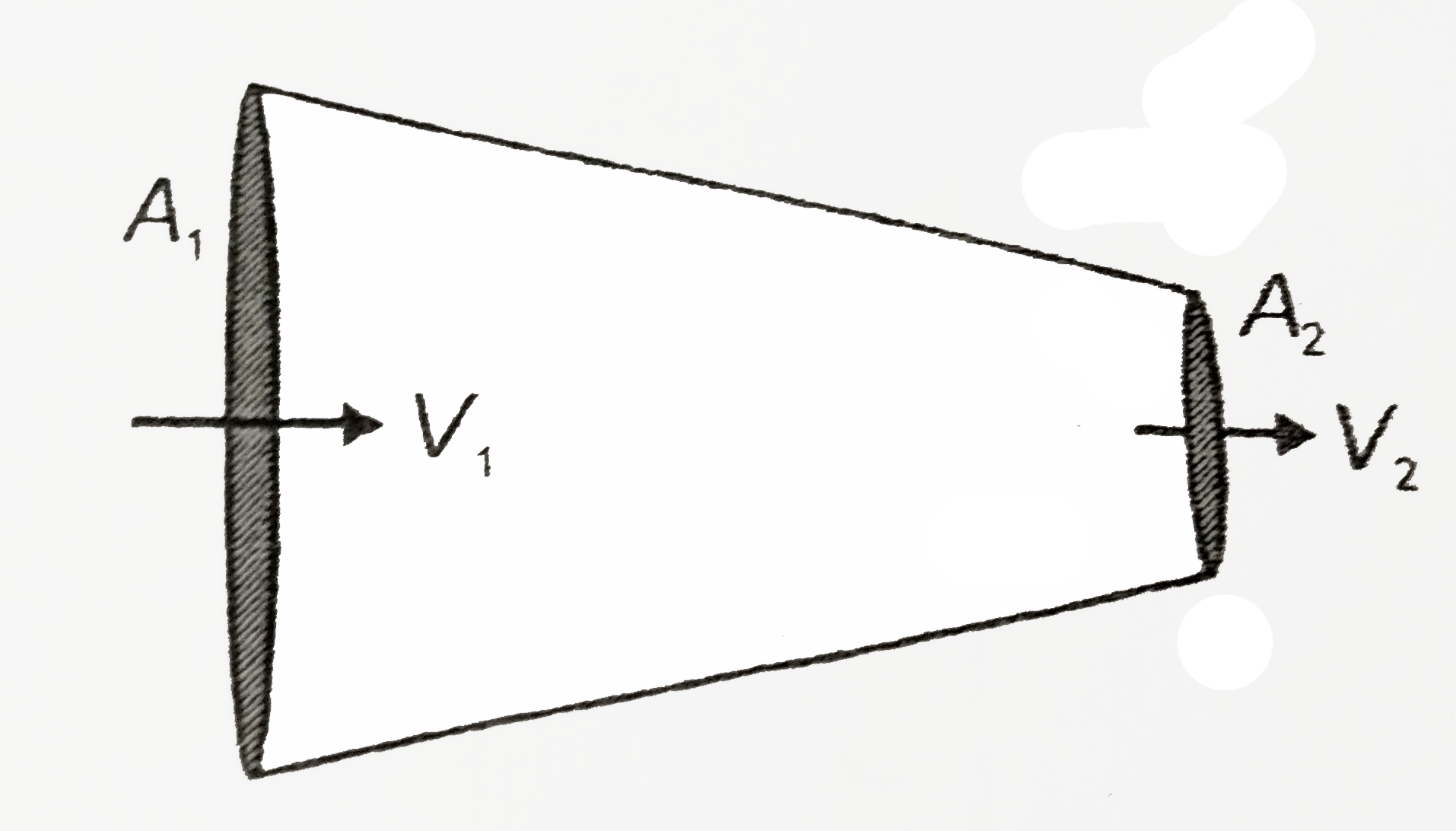
Calculate the rate of flow of glycerine of density. 1.25×103kg/m3 through the conical section of a pipe. If the radii of its ends are 1.0m and 0.04m and the pressure drop across its length is 10N/m2.
To solve the problem of calculating the rate of flow of glycerine through a conical section of a pipe, we will follow these steps:
Step 1: Identify Given Values
- Density of glycerine, ρ=1.25×103kg/m3
- Radius at the larger end, r1=1.0m
- Radius at the smaller end, r2=0.04m
- Pressure drop across the length, ΔP=P1−P2=10N/m2
Step 2: Use the Continuity Equation
The continuity equation states that the flow rate must be constant throughout the pipe. Therefore, we have:
A1V1=A2V2
Where A1 and A2 are the cross-sectional areas at the larger and smaller ends, respectively, and V1 and V2 are the fluid velocities at those points.
The areas can be calculated as:
A1=πr21=π(1.0)2=πm2
A2=πr22=π(0.04)2=π(0.0016)=0.005024m2
From the continuity equation, we can express the velocities in terms of each other:
V1=A2A1V2=0.005024πV2
Step 3: Use Bernoulli's Equation
According to Bernoulli's principle:
P1+12ρV21=P2+12ρV22
Rearranging gives:
P1−P2=12ρ(V22−V21)
Substituting the pressure drop:
10=12ρ(V22−V21)
Substituting ρ=1.25×103:
10=12(1.25×103)(V22−V21)
20=(1.25×103)(V22−V21)
V22−V21=201.25×103=0.016m2/s2
Step 4: Substitute V1 in Terms of V2
From the continuity equation, we have:
V1=0.005024πV2
Substituting V1 into the equation derived from Bernoulli's equation:
V22−(0.005024πV2)2=0.016
Let k=0.005024π:
V22−k2V22=0.016
V22(1−k2)=0.016
V22=0.0161−k2
Step 5: Calculate V2 and V1
Calculate k2:
k2=(0.005024π)2=0.00002524π2≈0.00002524/9.87≈0.00000256
Then,
V22=0.0161−0.00000256≈0.016
Thus,
V2≈0.128m/s
Now calculate V1:
V1=kV2≈0.005024π×0.128≈0.0002m/s
Step 6: Calculate the Rate of Flow Q
The flow rate Q can be calculated using:
Q=A2V2=π(0.04)2×0.128
Q=0.005024×0.128≈6.43×10−4m3/s
Final Answer
The rate of flow of glycerine through the conical section of the pipe is approximately:
Q≈6.43×10−4m3/s
- Density of glycerine, ρ=1.25×103kg/m3
- Radius at the larger end, r1=1.0m
- Radius at the smaller end, r2=0.04m
- Pressure drop across the length, ΔP=P1−P2=10N/m2
The continuity equation states that the flow rate must be constant throughout the pipe. Therefore, we have:
A1V1=A2V2
Where A1 and A2 are the cross-sectional areas at the larger and smaller ends, respectively, and V1 and V2 are the fluid velocities at those points.
A1=πr21=π(1.0)2=πm2
A2=πr22=π(0.04)2=π(0.0016)=0.005024m2
V1=A2A1V2=0.005024πV2
According to Bernoulli's principle:
P1+12ρV21=P2+12ρV22
Rearranging gives:
P1−P2=12ρ(V22−V21)
Substituting the pressure drop:
10=12ρ(V22−V21)
Substituting ρ=1.25×103:
10=12(1.25×103)(V22−V21)
20=(1.25×103)(V22−V21)
V22−V21=201.25×103=0.016m2/s2
From the continuity equation, we have:
V1=0.005024πV2
Substituting V1 into the equation derived from Bernoulli's equation:
V22−(0.005024πV2)2=0.016
Let k=0.005024π:
V22−k2V22=0.016
V22(1−k2)=0.016
V22=0.0161−k2
Calculate k2:
k2=(0.005024π)2=0.00002524π2≈0.00002524/9.87≈0.00000256
Then,
V22=0.0161−0.00000256≈0.016
Thus,
V2≈0.128m/s
V1=kV2≈0.005024π×0.128≈0.0002m/s
The flow rate Q can be calculated using:
Q=A2V2=π(0.04)2×0.128
Q=0.005024×0.128≈6.43×10−4m3/s
The rate of flow of glycerine through the conical section of the pipe is approximately:
Q≈6.43×10−4m3/s
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
21 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples
10 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Calculate the rate of flow of glycerine of density 1.25×103kg/m3 through the conical section of a pipe if the radii of its ends are 0.1m and 0.04 m and the pressure drop across its lengths is 10N/m2.
View SolutionCalculate the rate of flow of glycerine of density 1.25×103kgm−3 through the conical section of a pipe, if the radii of its ends are0.1 m and 0.04 m and the pressure drop across its length is 10Nm−2.
View Solution
Knowledge Check
The radii of curvatures of a convex lens are 0.04 m and 0.04m. Its refractive index is 1.5. Its focal length is
A0.04 mB0.4 mC4mD40 mTwo metal spheres are falling through a liquid of density 2×103kg/m3 with the same uniform speed. The material density of sphere 1 and sphere 2 are 8×103kg/m3 and 11×103kg/m3 respectively. The ratio of their radii is :-
A118B√118C32D√32A stress of 106N/m2 is required for breaking a material. If the density of the material is 3×103Kg/m3, then what should be the minimum length of the wire made of the same material so that it breaks by its own weight (g=10m/s2)
A33.4mB3.4mC34cmD3.4cm
Calculate the rate of flow of glycerine of density 1.20 ×103kg/m3 through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 Nm2.
View SolutionCalculate the moment of inertia of a cylinder of length 1.5m, radius 0.05m and density 8×103kg/m3 about the axis of the cylinder.
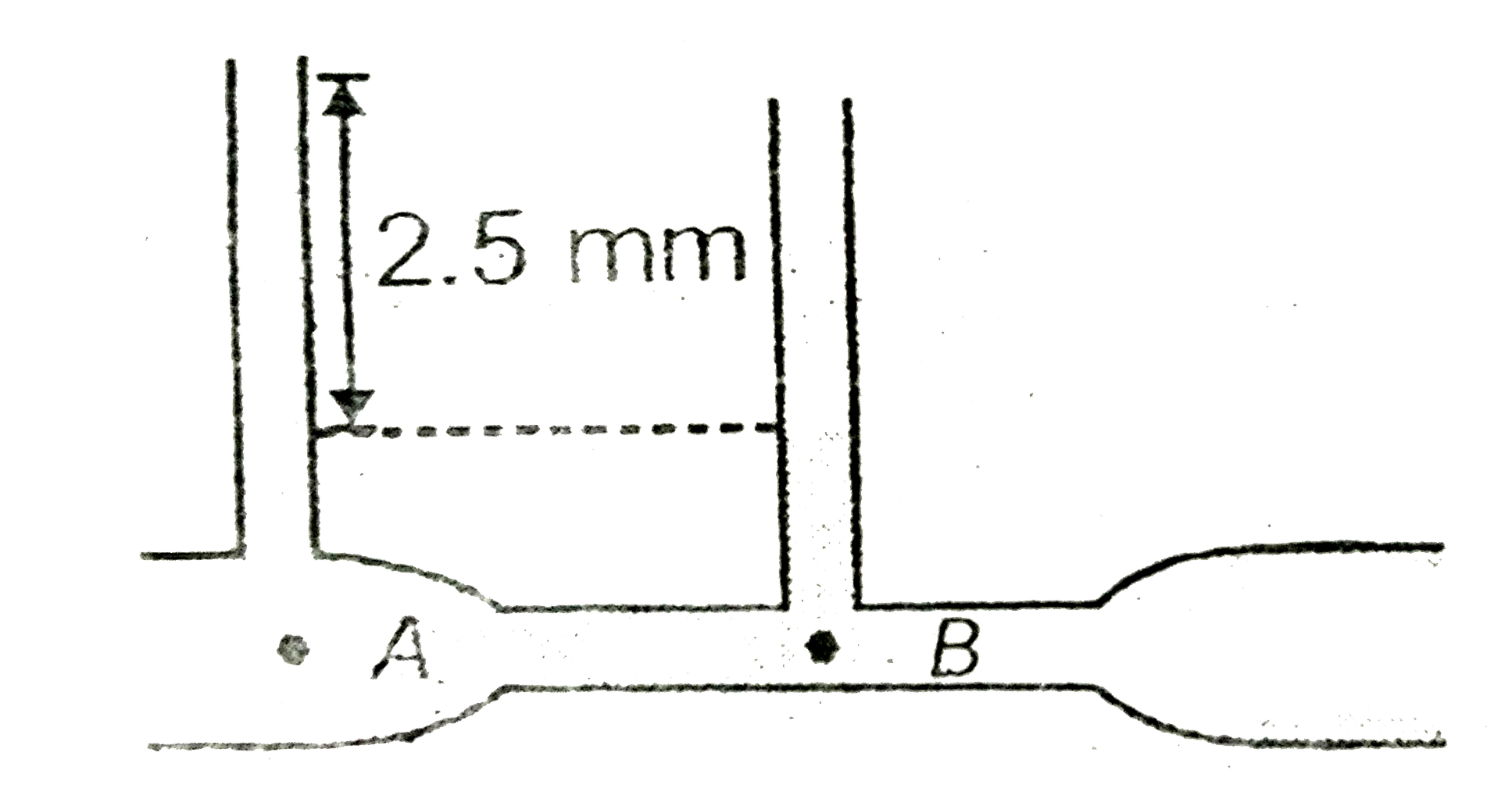
View SolutionIn the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
View SolutionCalculate the rate of flow (volume per second) of a liquid through a capillary tube of diameter 0.20×10−3m and length 1m,η=3.00×10−5Nm−2s and pressure gradient = 10 atm.
View SolutionA drop of radius 2×10−5 and density 1.2×103kg/m3 falls through air. The viscosity of air is 1.8×10−5Ns/m2. Neglecting buoyancy due to air, the terminal speed of the drop is
View Solution
