Can a process on an ideal gas be both adiabatic and isothermal. ?
To determine whether a process on an ideal gas can be both adiabatic and isothermal, we need to analyze the definitions and implications of both processes.
1. Define Adiabatic Process:
- An adiabatic process is one in which no heat is exchanged with the surroundings. This means that the heat transfer Q=0.
2. Define Isothermal Process:
- An isothermal process is one in which the temperature of the system remains constant throughout the process. This implies that the change in temperature ΔT=0.
3. Relate Temperature Change to Internal Energy:
- For an ideal gas, the internal energy U is a function of temperature. Therefore, if the temperature does not change (ΔT=0), the change in internal energy ΔU=0.
4. Apply the First Law of Thermodynamics:
- The first law of thermodynamics states:
Q=ΔU+W
where Q is the heat added to the system, ΔU is the change in internal energy, and W is the work done by the system.
5. Substitute Known Values:
- For an adiabatic process, Q=0. For an isothermal process, ΔU=0. Substituting these into the first law gives:
0=0+W
This implies that W=0, meaning no work is done by or on the gas.
6. Conclusion:
- If a process is both adiabatic and isothermal, it leads to the conclusion that there is no change in heat, no change in internal energy, and no work done. This situation is not physically realizable because a process implies some change. Therefore, it is not possible for a process on an ideal gas to be both adiabatic and isothermal simultaneously.
Summary:
In conclusion, a process on an ideal gas cannot be both adiabatic and isothermal because the conditions of both processes contradict each other. An adiabatic process requires no heat exchange, while an isothermal process requires a constant temperature, which necessitates heat exchange.
- An adiabatic process is one in which no heat is exchanged with the surroundings. This means that the heat transfer Q=0.
- An isothermal process is one in which the temperature of the system remains constant throughout the process. This implies that the change in temperature ΔT=0.
- For an ideal gas, the internal energy U is a function of temperature. Therefore, if the temperature does not change (ΔT=0), the change in internal energy ΔU=0.
- The first law of thermodynamics states:
Q=ΔU+W
where Q is the heat added to the system, ΔU is the change in internal energy, and W is the work done by the system.
- For an adiabatic process, Q=0. For an isothermal process, ΔU=0. Substituting these into the first law gives:
0=0+W
This implies that W=0, meaning no work is done by or on the gas.
- If a process is both adiabatic and isothermal, it leads to the conclusion that there is no change in heat, no change in internal energy, and no work done. This situation is not physically realizable because a process implies some change. Therefore, it is not possible for a process on an ideal gas to be both adiabatic and isothermal simultaneously.
In conclusion, a process on an ideal gas cannot be both adiabatic and isothermal because the conditions of both processes contradict each other. An adiabatic process requires no heat exchange, while an isothermal process requires a constant temperature, which necessitates heat exchange.
Topper's Solved these Questions
Similar Questions
The reversible expansion of an ideal gas under adiabatic and isothermal conditions is shown in the figure. Which of the following statement(s) is (are) correct?
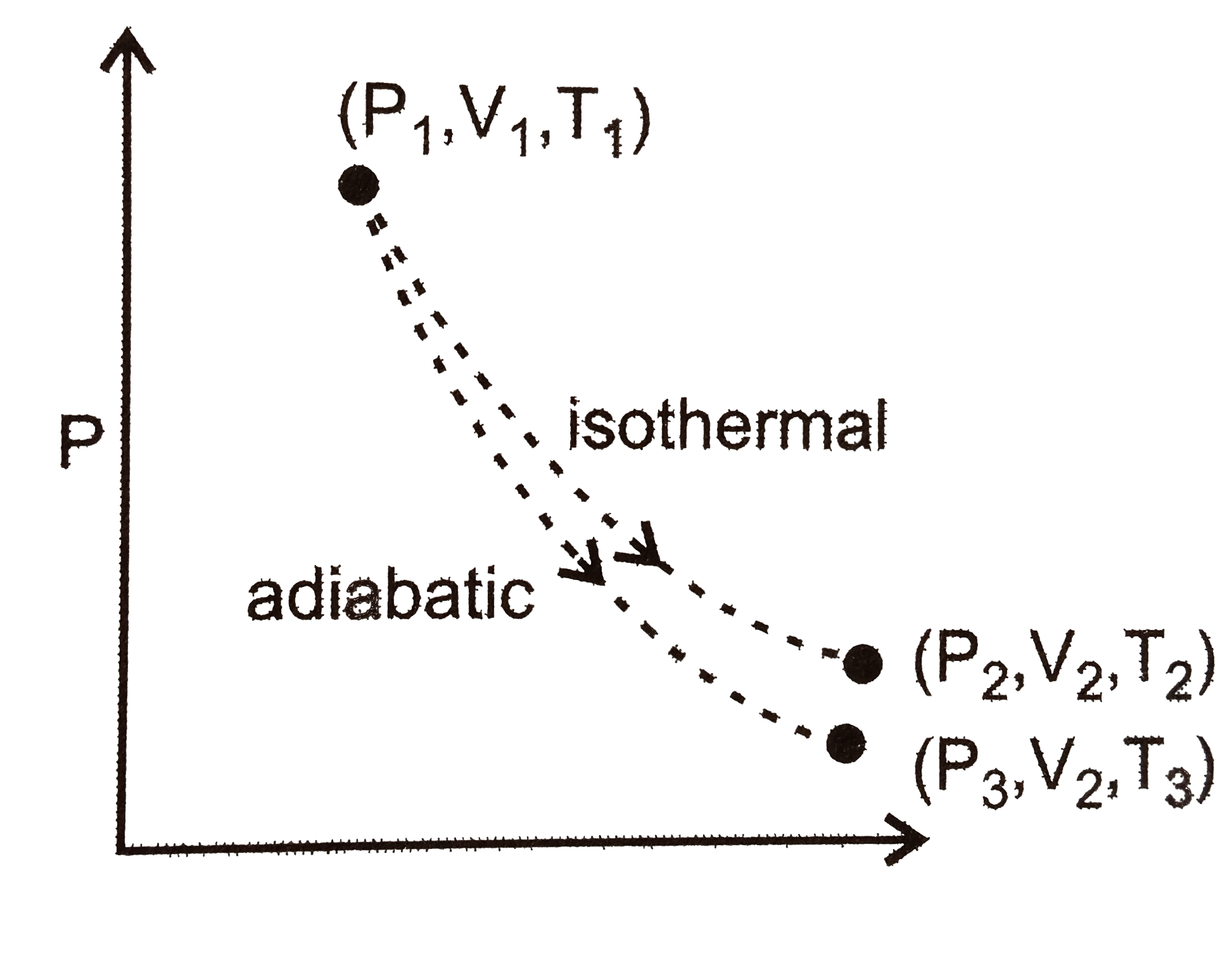
View SolutionCan two states of an ideal gas be connected by an isothermal process as well as an adiabatic process?
View SolutionAn ideal gas undergoes a process consisting of adiabatic and isothermal process only as shown in the figure. Then :
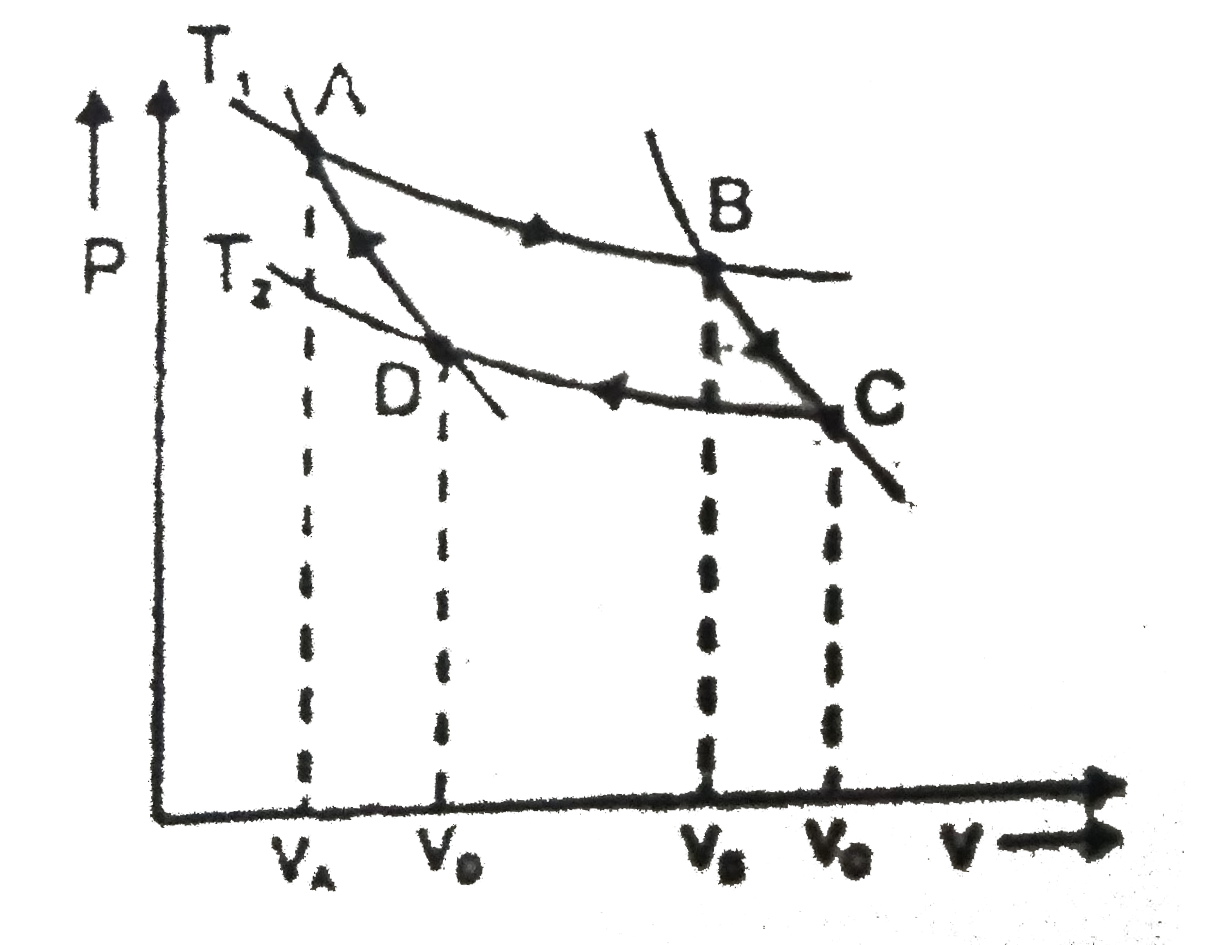
View SolutionIn an isothermal process for an ideal gas
View SolutionLet F1 be the magnitude of the gravitational force exerted on the Sun by Earth and F2 be the magnitude of the force exerted on Earth by the Sun. Then:
View SolutionAn ideal gas is expended adiabatically then
View SolutionLet Q and W denote the amount of heat given to an ideal gas the work done by it in an isothermal process.
View SolutionThe curves A and B in the figure shown P-V graphs for an isothermal and an adiabatic process for an idea gas. The isothermal process is represented by the curve A.
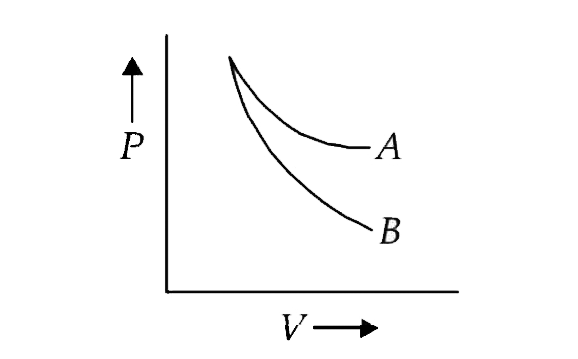
View SolutionThe curves A and B in the figure shown P-V graphs for an isothermal and an adiabatic process for an idea gas. The isothermal process is represented by the curve A.

View SolutionTotal internal energy of an ideal gas remains constant in isothermal process.
View Solution
