Charge q is uniformly distributed on a disc of radius r. If the disc is rotated with a frequency v, then magnetic field induction at the centre will be
μ0qvr
μ0qvr
μ0vqr
μ0qvr
The correct Answer is:B
Consider a small element of the disc of radius x with dx, figure. Face area of the small element of disc =2πxdx
Charge on the elementary part of disc,
dq=qπr2×2πxdx or dq=2qxdxr2

Magnetic field induction at O due to rotation of elementary ring with frequency v is
dB=μ04π2πdqvx(∵dI=dq×v)'<br>'=μ02x×2qxdxr2×v=μ0qvr2dx
∴ Total magnetic field conduction at O due to rotation of whole disc with frequency is
B=∫r0μ0qvr2dx=μ0qvr2(r−0)=μ0qvr
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (a)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (c)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Value Based Questions2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
A plastic disc of radius 'R' has a charge 'q' uniformly distributed over its surface. If the dis is rotated with a frequency 'f' about its axis, then the magnetic induction at the centre of the disc is given by
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View Solution
Knowledge Check
- Question 1 - Select One
Charges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
Aq2π2ε0R2Bq4π2ε0R2Cq4πε0R2Dq2πε0R2 - Question 2 - Select One
A charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
A B
B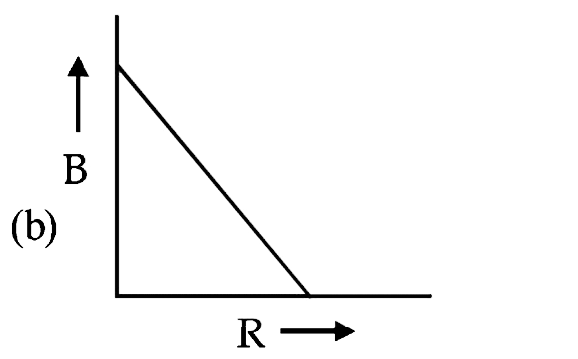 C
C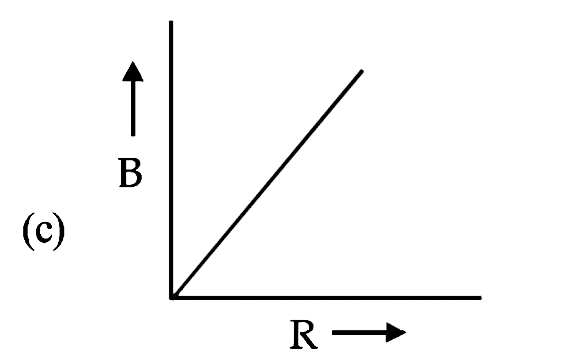 D
D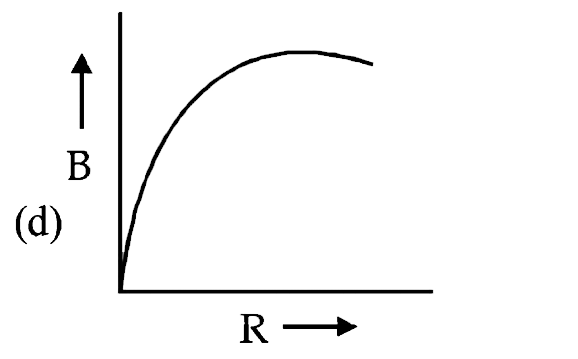
- Question 3 - Select One
Charge q is uniformly spreade on a thin ring of radius R. The ring rotates about its axis with a uniform frequency f Hz. The magnitude of magnetic induction at the centre of the ring is
Aμ0qf2πRBμ0qf2RCμ0q2fRDμ0q2πfR
There is a hemispherical shell having charge Q uniformly distributed on its surface. Radius of the shell is R. Find electric potential and field at the centre (of the sphere).
View SolutionCharge q is uniformly spread on a thin ring of radius R. The ring rotates about its axis with a uniform frequency f Hz. The magnitude of magnetic induction at the center of the ring is:
View SolutionA rod of length l having uniformly distributed charge Q is rotated about one end with constant frequency f Its magnetic moment
View SolutionA flat circular fixed disc has charge +Q uniformly distributed on the disc. A charge +q is thrown with kinetic energy K, towards the disc along its axis. The charge q :
View SolutionA charge Q is uniformly distributed in a dielectric sphere of radius R (having dielectric constant unity). This dielectric sphere is enclosed by a concentric spherical shell of radius 2R and having uniformly distributed charge 2Q. Which of the following graph correctly represents variation of electric field with distance r from the common centre?
 View Solution
View Solution

