Choose the correct statement(s)
A dimensionally correct equation may be correct
A dimensionally correct equation may be incorrect
A dimensionally incorrect equation may be correct
A dimensionally incorrect equation may be incorrect.
The correct Answer is:A, B, D
To solve the question of choosing the correct statements regarding dimensional analysis, we will analyze each option step by step.
1. Understanding Dimensional Analysis:
- Dimensional analysis is a method used to check the consistency of physical equations by comparing the dimensions of the quantities involved.
2. Evaluating Option 1:
- Statement: "A dimensionally correct equation may be correct."
- Example: Consider the equation for speed, v=dt, where d is distance and t is time.
- Dimensions:
- Speed (v)=LT−1
- Distance (d)=L
- Time (t)=T
- Since both sides have the same dimensions, this equation is dimensionally correct, and it is also a correct physical equation.
- Conclusion: This statement is correct.
3. Evaluating Option 2:
- Statement: "A dimensionally correct equation may be incorrect."
- Example: Consider momentum p=mv and impulse I=F⋅t.
- Dimensions:
- Momentum (p)=MLT−1
- Impulse (I)=MLT−1
- Both have the same dimensions, but p≠I. Therefore, a dimensionally correct equation can indeed be incorrect.
- Conclusion: This statement is correct.
4. Evaluating Option 3:
- Statement: "A dimensionally incorrect equation may be correct."
- Example: Consider the equation F=mv (force equals mass times velocity).
- Dimensions:
- Force (F)=MLT−2
- Right-hand side (mv)=MLT−1
- The dimensions do not match, indicating the equation is dimensionally incorrect. Thus, it cannot be a correct physical equation.
- Conclusion: This statement is incorrect.
5. Evaluating Option 4:
- Statement: "A dimensionally incorrect equation may be incorrect."
- As established, for an equation to be correct, its dimensions must also be correct. Therefore, if an equation is dimensionally incorrect, it is likely to be incorrect.
- Conclusion: This statement is correct.
Final Conclusion:
The correct options are:
- Option 1: A dimensionally correct equation may be correct.
- Option 2: A dimensionally correct equation may be incorrect.
- Option 4: A dimensionally incorrect equation may be incorrect.
Thus, the correct statements are Option 1, Option 2, and Option 4.
- Dimensional analysis is a method used to check the consistency of physical equations by comparing the dimensions of the quantities involved.
- Statement: "A dimensionally correct equation may be correct."
- Example: Consider the equation for speed, v=dt, where d is distance and t is time.
- Dimensions:
- Speed (v)=LT−1
- Distance (d)=L
- Time (t)=T
- Since both sides have the same dimensions, this equation is dimensionally correct, and it is also a correct physical equation.
- Conclusion: This statement is correct.
- Statement: "A dimensionally correct equation may be incorrect."
- Example: Consider momentum p=mv and impulse I=F⋅t.
- Dimensions:
- Momentum (p)=MLT−1
- Impulse (I)=MLT−1
- Both have the same dimensions, but p≠I. Therefore, a dimensionally correct equation can indeed be incorrect.
- Conclusion: This statement is correct.
- Statement: "A dimensionally incorrect equation may be correct."
- Example: Consider the equation F=mv (force equals mass times velocity).
- Dimensions:
- Force (F)=MLT−2
- Right-hand side (mv)=MLT−1
- The dimensions do not match, indicating the equation is dimensionally incorrect. Thus, it cannot be a correct physical equation.
- Conclusion: This statement is incorrect.
- Statement: "A dimensionally incorrect equation may be incorrect."
- As established, for an equation to be correct, its dimensions must also be correct. Therefore, if an equation is dimensionally incorrect, it is likely to be incorrect.
- Conclusion: This statement is correct.
The correct options are:
- Option 1: A dimensionally correct equation may be correct.
- Option 2: A dimensionally correct equation may be incorrect.
- Option 4: A dimensionally incorrect equation may be incorrect.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises19videos
INTRODUCTION TO PHYSICS
- BOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer4videos
INTRODUCTION TO PHYSICS
- BOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Objective 16videos
INTRODUCTION TO PHYSICS
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER11videos
HEAT TRANSFER
- BOOK - HC VERMA ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - All Questions106videos
KINETIC THEORY OF GASES
Similar Questions
A curved surface of radius R separates two medium of refractive indices μ1andμ2 as shown in figures A and B .
_E01_077_Q01.png)
Choose the correct statement(s) related to the real image formed by the object O placed at a distance x, as shown in figure A.View SolutionA curved surface of radius R separates two medium of refractive indices μ1andμ2 as shown in figures A and B .
_E01_078_Q01.png)
Choose the correct statement(s) related to the virtual image formed by object O placed at a distance x, as shown in figureView SolutionChoose the correct statements(s):
View SolutionConsider the following compounds:

Choose the correct statements(s) from the following:View Solution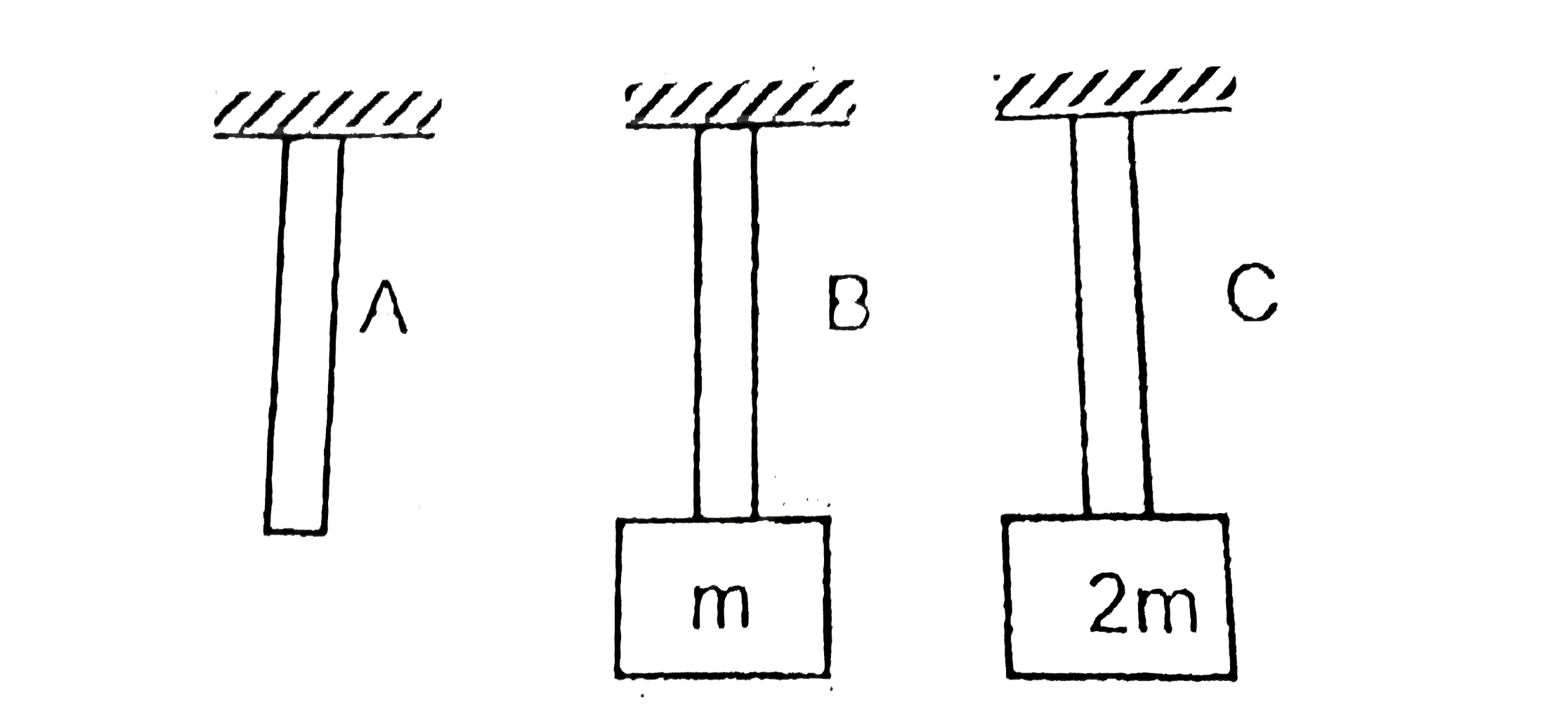
Consider the three ropes of same length and same linear density as (shown in figure) suspended from the ceiling.
A pulse is generated at the lowest point of the three ropes simultaneously. Choose the correct statements(s)View SolutionThe instantaneous charge on capacitor in two discharging RC circuils is plotted with respect to time in figure. Choose the correct statement (s) (where E1 and E2 are emfs of two DC sources in two different charging circuits and capacitors are fully charged ).
 View Solution
View Solution
In the adjacent figure blocks A and B of weight W each are lying at rest on a rough horizontal surface. They are pulled by applying forces F1 and F2 as shown in figure. When blocks are in limiting equilibrium F2=5F1 Choose the correct statement (s) (Assume same coefficient of friction for both the blocks)View SolutionChoose the correct statements.
View SolutionChoose the correct statements
View SolutionThe temperature coefficient of the cell is (∂E∂T)P. Choose the correct statements (s).
View Solution
