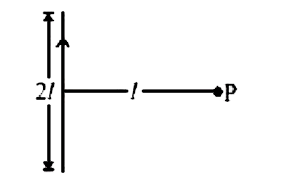
Consider a straight piece of length x of a wire carrying a current i. Let P be a point on the perpendicular bisector of the piece, situated at a distance d from its middle point. Show that for dgtgtx, the magnetic field at P varies as (1d2) whereas for dltltx, it varies as 1/d.
Since O is the mid point of MN=l.
So , B=μoi4π. 2l√l2+4d2.
If d>>x,thusB=μoi4πd. 2l2d.
i.e. B∝1d .

Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 27videos
MAGNETIC FIELD DUE TO CURRENT
- BOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises61videos
MAGNETIC FIELD
- BOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises9videos
MAGNETIC PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
A long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
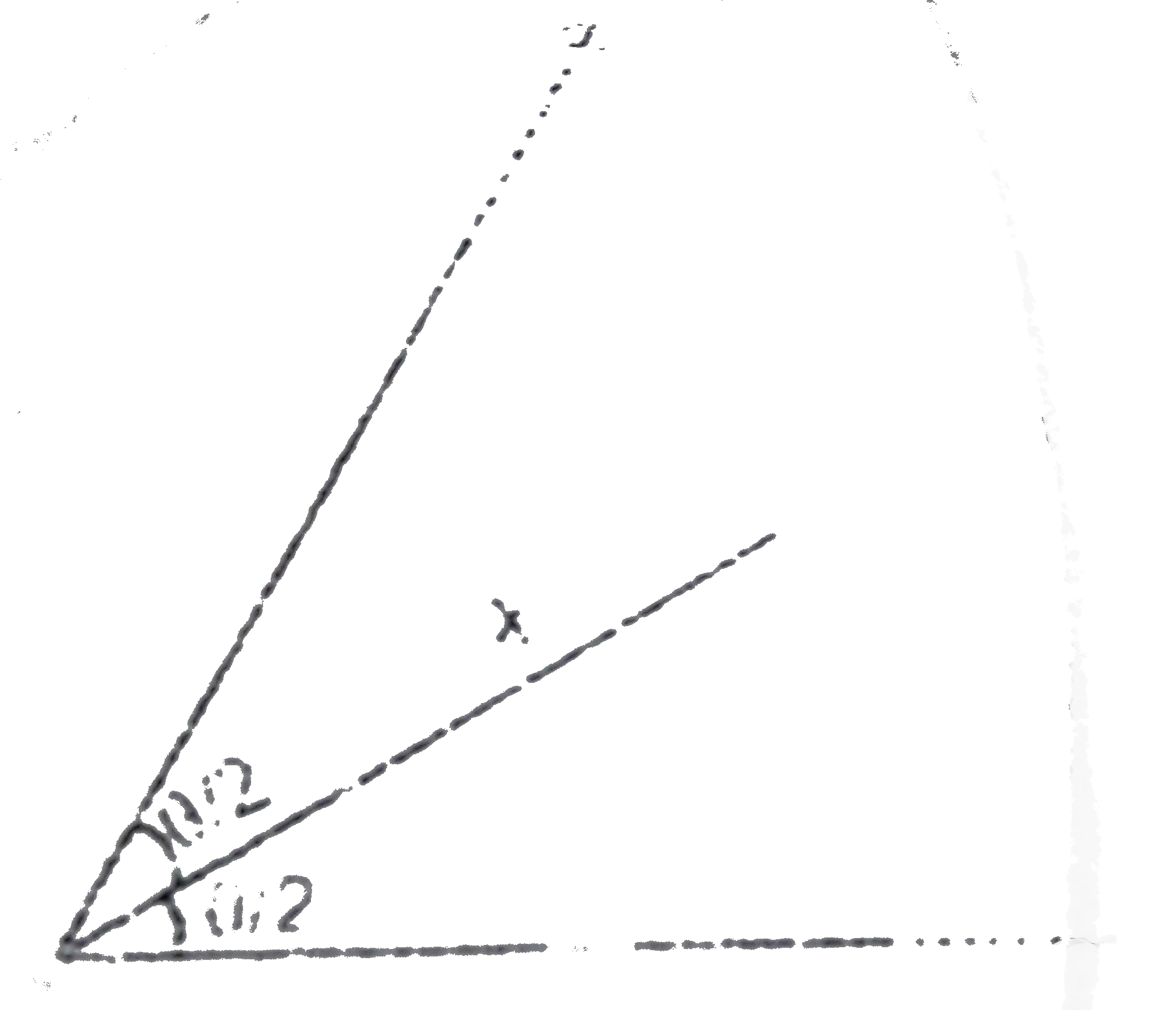 Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙
Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙ - Question 2 - Select One
Figure shows a straight wire of length l carrying a current i. Find the magnitude of magnetic field produced by the current at point P.
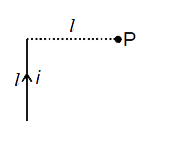 A√2μ0i3π1B√2μ0i8π1Cμ0i2π1D√2μ0iπl
A√2μ0i3π1B√2μ0i8π1Cμ0i2π1D√2μ0iπl - Question 3 - Select One
The magnetic field due to current in a straight wire segment of length L at a point on its perpendicular bisector at a distance r(r>>L)
Adecreases as 1rBdecreases as tr2Cdecreases as 1r3Dapproaches a finite limit as r→∞
Derive an expression fro the gravitational field due to a unifrom rod of length L and M at a point on its perpendicular bisector at a distance d from the centre.
View SolutionA straight metal wire of length L is carrying a current i.
Calculate the magnetic field intensity due to this wire at a point which is at the same distance from both ends of the rod and equal to length of road.View SolutionFind magnitude and direction of magnetic field at point P in the following cases.
(a)
(b)
P is the centre of square.
(c)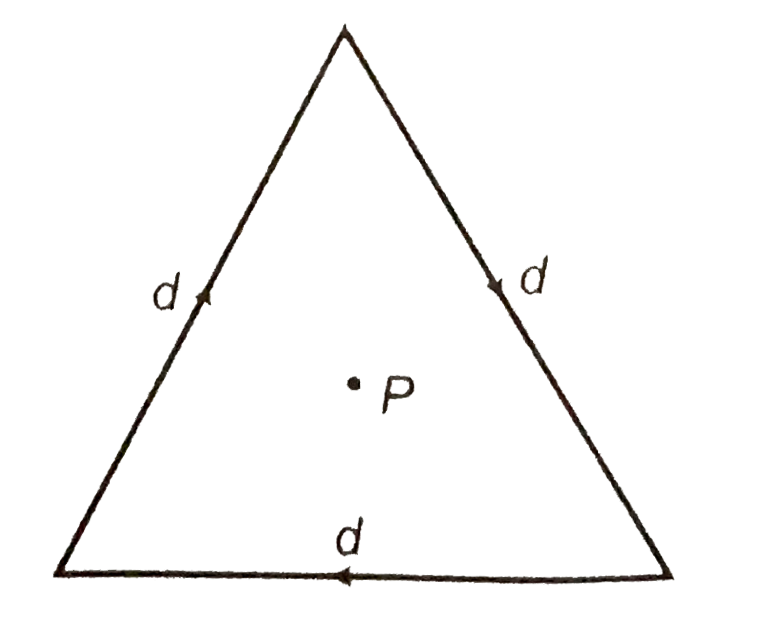
P is the centre of equilateral triangle.
(d)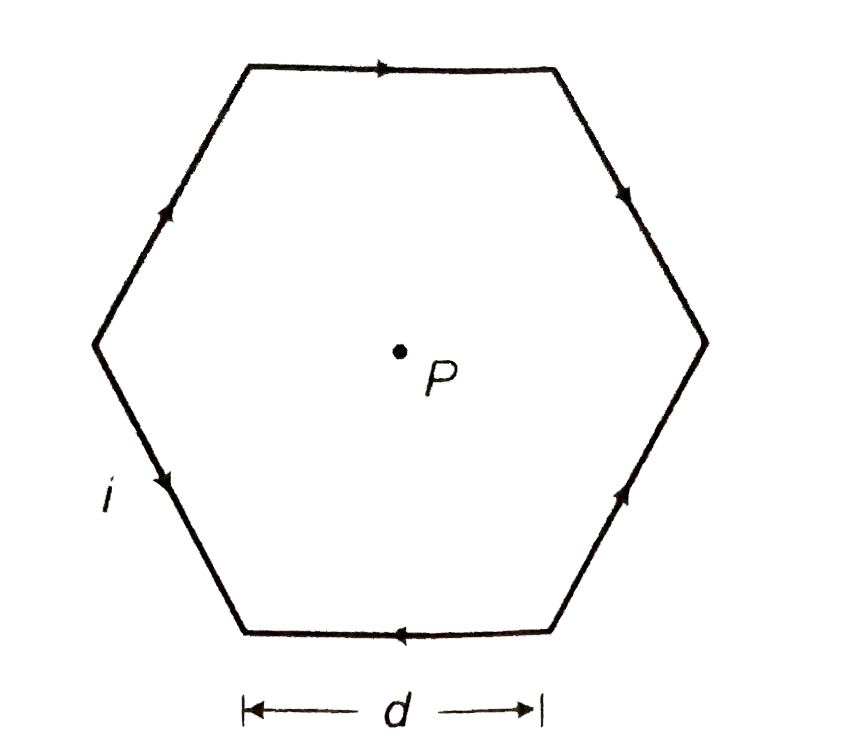
P is the centre of regular hexagon.
(e)
P is the centre of rectangular loop.
(f)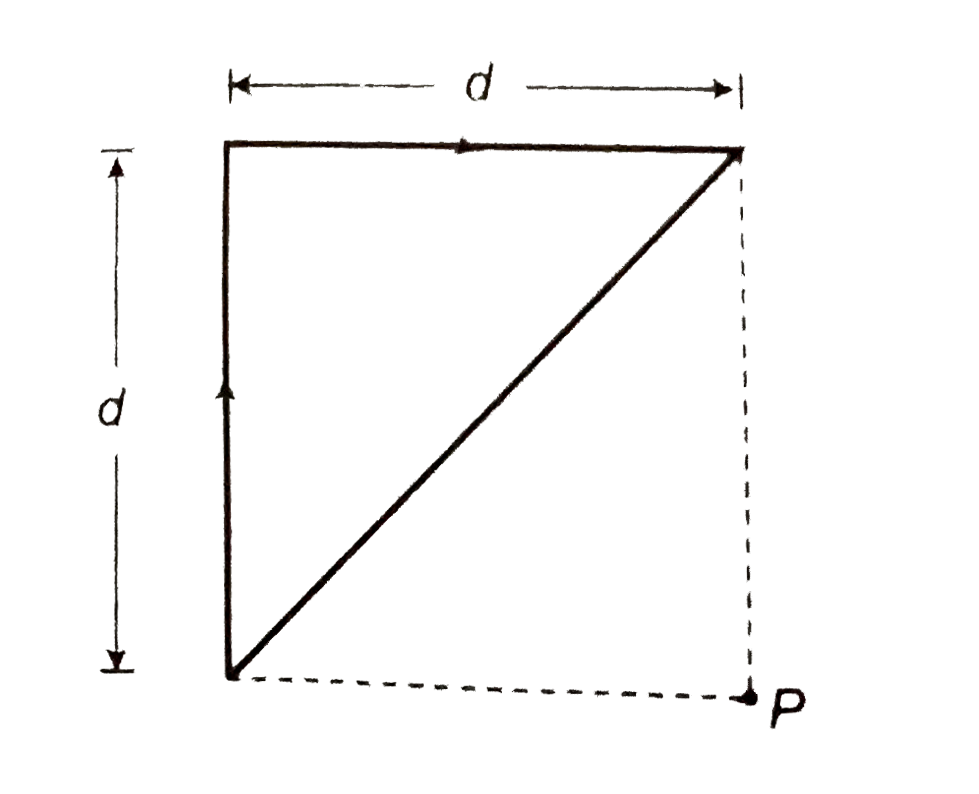
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.View SolutionA straight wire of finite length carrying current I subtends an angle of 60∘ at point P as shown. The magnetic field at P is
 View Solution
View SolutionA long straight wire, carrying current I, is bent at its midpoint to form an angle of 45∘. Find the induction of magnetic field at point P, distant R from the point of bending (as shown in)
 View Solution
View Solution