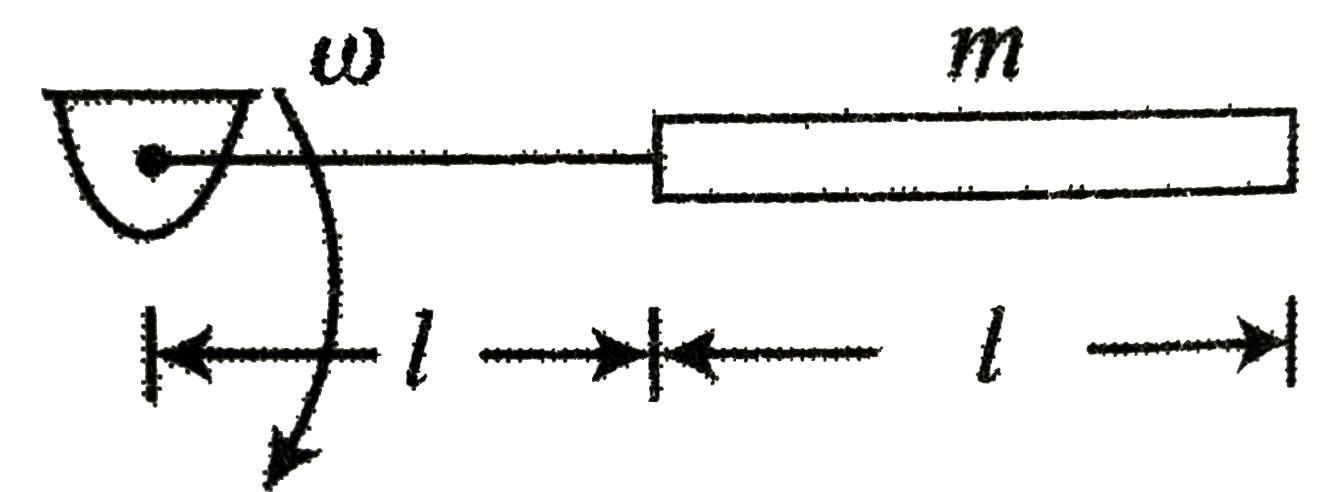
Consider a variation of the previous problem. Suppose the circular loo

Topper's Solved these Questions

BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9videos
ELECTROMAGNETIC INDUCTION
BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10videos
ELECTROMAGNETIC INDUCTION
BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75videos
ELECTRIC FIELD AND POTENTIAL
BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9videos
ELECTROMAGNETIC WAVES

Knowledge Check

Question 1 - Select One
Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed $(ω)$ as shown in the figure. Find the current in the rod when $- A O C = 90^{\circ}$
A $\frac{5}{3} \frac{B a^{2} ω}{R}$
B $\frac{8}{3} \frac{B a^{2} ω}{R}$
C $\frac{B a^{2} ω}{3 R}$
DNone of these
Question 2 - Select One
Figure shows a situation similar to the previous problem. All parameters are the same except that a battery of emf $ε$ and a variable resistance R are connected between O and C. The connecting wires have zero resistance. No external force is applied on the rod (except gravity, forces by the magnetic field and by the pivot).

In what way should the resistance R be changed so that the rod may rotate with uniform angular velocity in the clockwise direction? Express your answer in terms of the given quantities and the angle $(θ)$ made by the rod OA with the horizontal.
A $(B ω a^{2} - 2 ε) \frac{a B}{2 m g cos θ}$
B $(B ω a^{2} + 2 ε) \frac{a B}{m g cos θ}$
C $(B ω a^{2} + 2 ε) \frac{a B}{2 m g cos θ}$
DNone of these
Question 3 - Select One or More
A thin uniform rod of mass $m$ and length $L$ rotates with the constant angular velocity $ω$ about .the vertical axis passing through the rod's suspensjon point $O$ . It describes a carried surface, then:
Acentrifugal force acting on rod is $m \frac{L}{2} sin θ ω^{2}$ and will pass through centre of mass
Bcentrifugal force acting on rod is $m \frac{L}{2} sin θ ω^{2}$ and will not pass through centre of mass
C $θ = {cos}^{- 1} (\frac{3 g}{2 ω^{2} L})$
D $θ = {cos}^{- 1} (\frac{g}{ω^{2} L})$

We know that $< b r > F = \frac{B^{2} a^{2} ω}{2 R} = i B l$
$C o m p o \neq n t o f m g a l o n g F = m g sin θ$
$N e t f or c e = \frac{B^{2} a^{2} ω}{2 R} - m g sin θ .$

Topper's Solved these Questions

Similar Questions

Knowledge Check

A thin uniform rod of mass $m$ and length $L$ rotates with the constant angular velocity $ω$ about .the vertical axis passing through the rod's suspensjon point $O$ . It describes a carried surface, then:

HC VERMA-ELECTROMAGNETIC INDUCTION-Exercises

We know that <br>F=B2a2ω2R=iBl Compo≠ntofmgalongF=mgsinθ Netforce=B2a2ω2R−mgsinθ.

Topper's Solved these Questions

Similar Questions

Knowledge Check

A thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:

HC VERMA-ELECTROMAGNETIC INDUCTION-Exercises

We know that $< b r > F = \frac{B^{2} a^{2} ω}{2 R} = i B l$
$C o m p o \neq n t o f m g a l o n g F = m g sin θ$
$N e t f or c e = \frac{B^{2} a^{2} ω}{2 R} - m g sin θ .$

A thin uniform rod of mass $m$ and length $L$ rotates with the constant angular velocity $ω$ about .the vertical axis passing through the rod's suspensjon point $O$ . It describes a carried surface, then: