Consider an object of mass M that is small enough to be treated as a particle but large enough that a section of mass m can be removed and positioned 3.0 mm from the remaining part. To maximize the magnitude of the gravitational force between the removed section and the remaining part, what should the ratio of m/M be?
To solve the problem of maximizing the gravitational force between the removed section of mass m and the remaining part of mass M, we can follow these steps:
Step 1: Write the formula for gravitational force
The gravitational force F between two masses m and M separated by a distance r is given by Newton's law of gravitation:
F=G⋅m⋅Mr2
where G is the gravitational constant and r is the distance between the two masses.
Step 2: Substitute the given values
In this scenario, the distance r is given as 3 mm, which we convert to meters:
r=3 mm=3×10−3 m
Thus, the gravitational force can be expressed as:
F=G⋅m⋅M(3×10−3)2
Step 3: Simplify the expression
We can simplify the expression for gravitational force:
F=G⋅m⋅M9×10−6
Step 4: Differentiate the force with respect to m
To maximize the gravitational force, we differentiate F with respect to m:
dFdm=G⋅M9×10−6⋅1
Since G and M are constants, we can ignore them while differentiating.
Step 5: Set the derivative to zero
To find the maximum, we set the derivative equal to zero:
dFdm=0
This implies that the force is maximized when the mass m is a certain fraction of M.
Step 6: Use the relationship between m and M
From the differentiation, we find that the gravitational force is maximized when:
m=M2
Step 7: Find the ratio mM
Now, we can find the ratio of m to M:
mM=M/2M=12
Final Answer
Thus, the ratio of m to M that maximizes the gravitational force is:
mM=12
The gravitational force F between two masses m and M separated by a distance r is given by Newton's law of gravitation:
F=G⋅m⋅Mr2
where G is the gravitational constant and r is the distance between the two masses.
In this scenario, the distance r is given as 3 mm, which we convert to meters:
r=3 mm=3×10−3 m
Thus, the gravitational force can be expressed as:
F=G⋅m⋅M(3×10−3)2
We can simplify the expression for gravitational force:
F=G⋅m⋅M9×10−6
To maximize the gravitational force, we differentiate F with respect to m:
dFdm=G⋅M9×10−6⋅1
Since G and M are constants, we can ignore them while differentiating.
To find the maximum, we set the derivative equal to zero:
dFdm=0
This implies that the force is maximized when the mass m is a certain fraction of M.
From the differentiation, we find that the gravitational force is maximized when:
m=M2
Now, we can find the ratio of m to M:
mM=M/2M=12
Thus, the ratio of m to M that maximizes the gravitational force is:
mM=12
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)16videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)7videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - CHECKPOINT5videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)4videos
GEOMETRICAL OPTICS : REFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)5videos
HEAT-MEASUREMENT AND TRANSFER
Similar Questions
A particle of mass m is situated at a distance d from one end of a rod of mass M and length L as shown in diagram. Find the magnitude of the gravitational force between them
 View Solution
View SolutionAn infinite number of particles each of mass m are placed on the positive X-axis of 1m,2m,4m,8m,... from the origin. Find the magnitude of the resultant gravitational force on mass m kept at the origin.
View Solution
Knowledge Check
- Question 1 - Select One
A mass M splits into two parts m and (M-m), which are separated by a cetain distance. The ratio m/M which maximizes the gravitational force between the parts is
A1:4B1:3C1:2D1:1 - Question 2 - Select One
A mass M splits into two parts m and (M - m) , which are then separated by a certain distance. Wha ratio (m/M) maximize the gravitational force between the path ?
A23B34C12D13 - Question 3 - Select One
Two particle of masses m and 2m are at a distance 3r apart at the ends of a straight line AB. C is the centre of mass of the system. The magnitude of the gravitational force on a unit mass placed at C due to the masses is
AzeroB7Gm4r2C9Gm4r2D3Gm2r2
A particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionFour point masses each of mass 'm' are placed on the corner of square of side 'a' Calculate magnitude of gravitational force experienced each particle
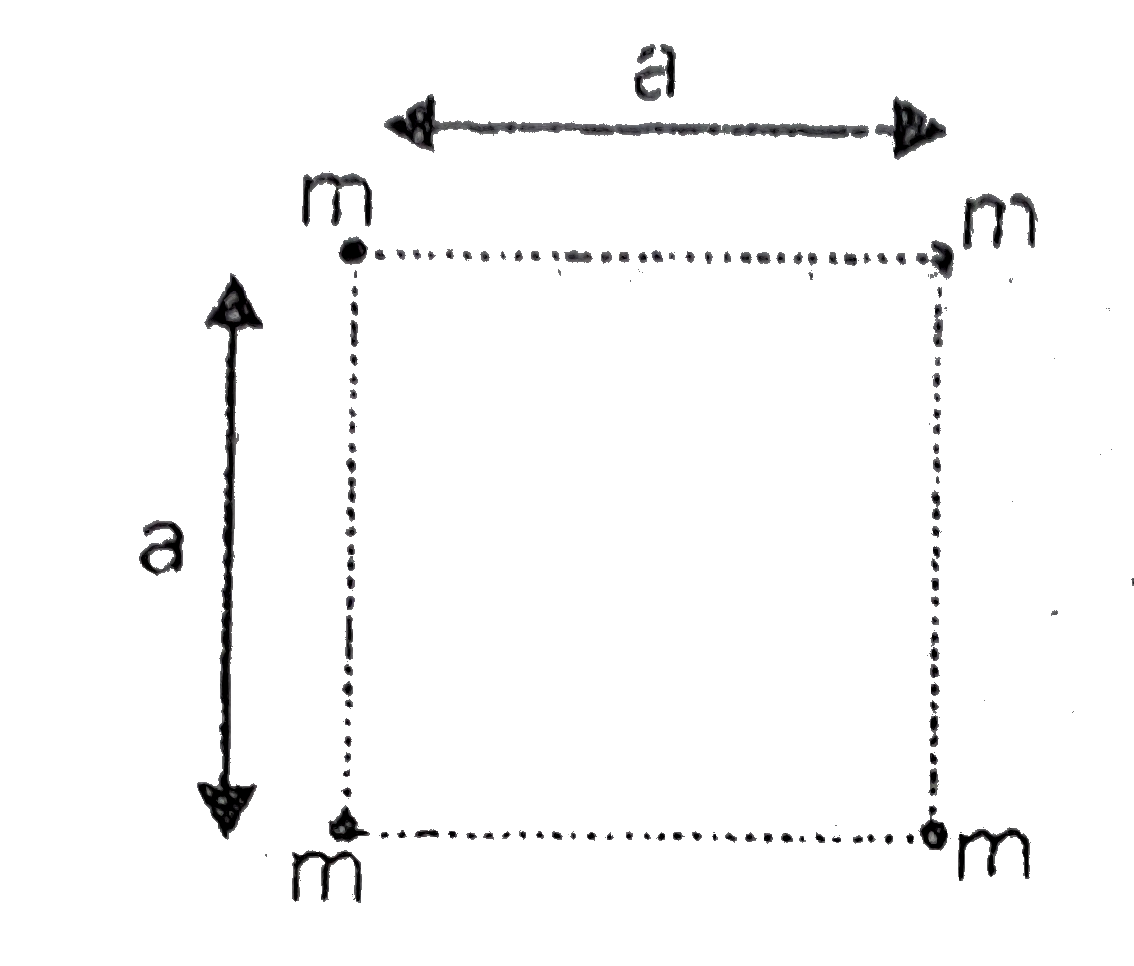 .View Solution
.View SolutionA uniform ring of mass m is lying at a distance √3 a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
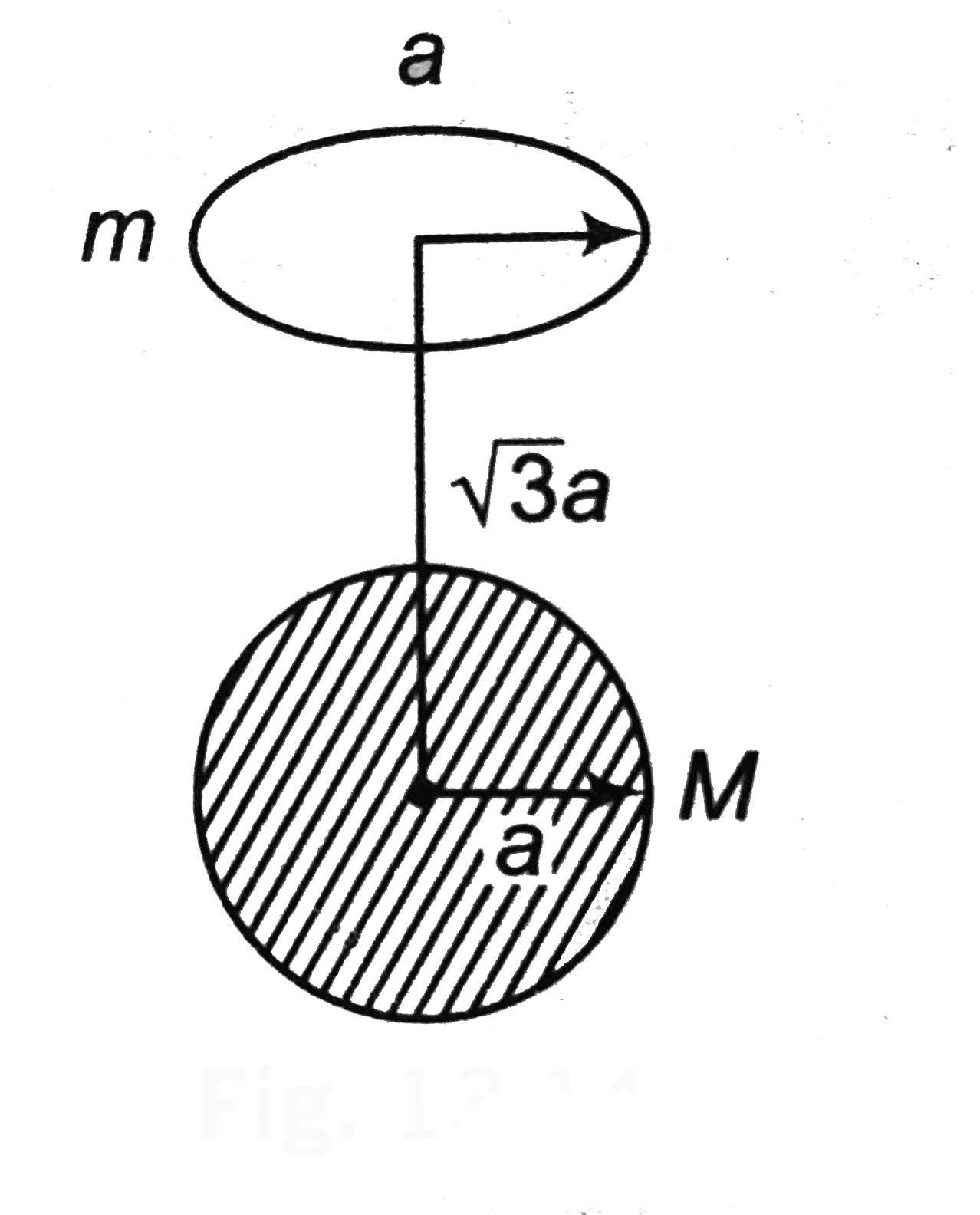 View Solution
View SolutionTwo point masses m and M are separated by a distance d. If the separation d remains fixed and the masses are increased to the values 3m and 3M, respectively, how does the gravitational force between them change ?
View SolutionThe gravitational force between two particles of masses m1 and m2 separeted by the same distance, then the gravitational force between them will be
View Solution

