In 1610, Galileo used his telescope to discover four moons around Jupiter, with these mean orbital radii a and periods T.
(a) Plot log a (y axis) against log T (x axis) and show that you get a straight line. (b) Measure the slope of the line and compare it with the value that you expect from Kepler's third law. (c) Find the mass of Jupiter from the intercept of this line with the y axis.
Text Solution
(a) log(rE/a)
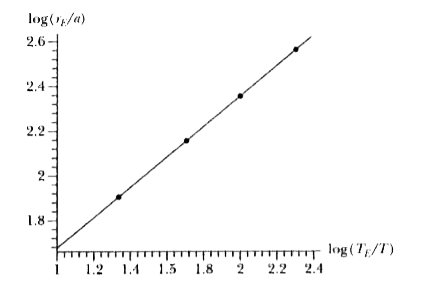
(b) Slope = 2/3 , (c ) 1.86×1027kg
|
Topper's Solved these Questions
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
16 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
7 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - CHECKPOINT
5 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)
4 Videos
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)
5 Videos
Similar Questions
Knowledge Check
The graph between the log K versus 1T is a straight line. The slope of the line is
A−2.303REaB−Ea2.303RC2.303REaDEa2.303RBy plotting log x/m on y-axis and log P on x-axis we s hould get
A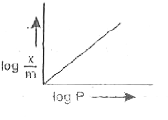 B
B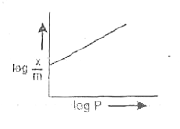 C
C D
D
A plot of log (xm) against log P for the adsorption of a gas on a sloid gives a straight a straight line with slope equal to :
A1nBnClogKDK
A plot of ln k against 1T (abscissa) is expected to be a straight line with intercept on coordinate axis equal to
View SolutionFor a first order reaction, the plot of log k against 1/T is a straight line. The slope of the line is equal to
View SolutionA plot of ln k against 1T (abscissa) is expected to be a straight line with intercept on coordinate axis equal to
View SolutionA plot of log (a-x) against time 't' is a straight line. This indicates that the reaction is of :
View SolutionA plot of log (a-x) against time 't' is a straight line. This indicates that the reaction is of :
View Solution
