Consider one mole of a perfect gas in a cyclinder of unit cross section with a piston attached, (figure) A spring (spring constant K) is attached (unstretched length ) to the piston and the bottom of the cylinder. Initially, the spring is unstretched and the gas is in equilibrium. A certain amount of heat is supplied to the gas causing an increase of volume from .
(a) What is the initial pressure of the system?
(b) What is the final pressure of the system?
(c) Using the first law of thermodynamics, write down a relation between and .
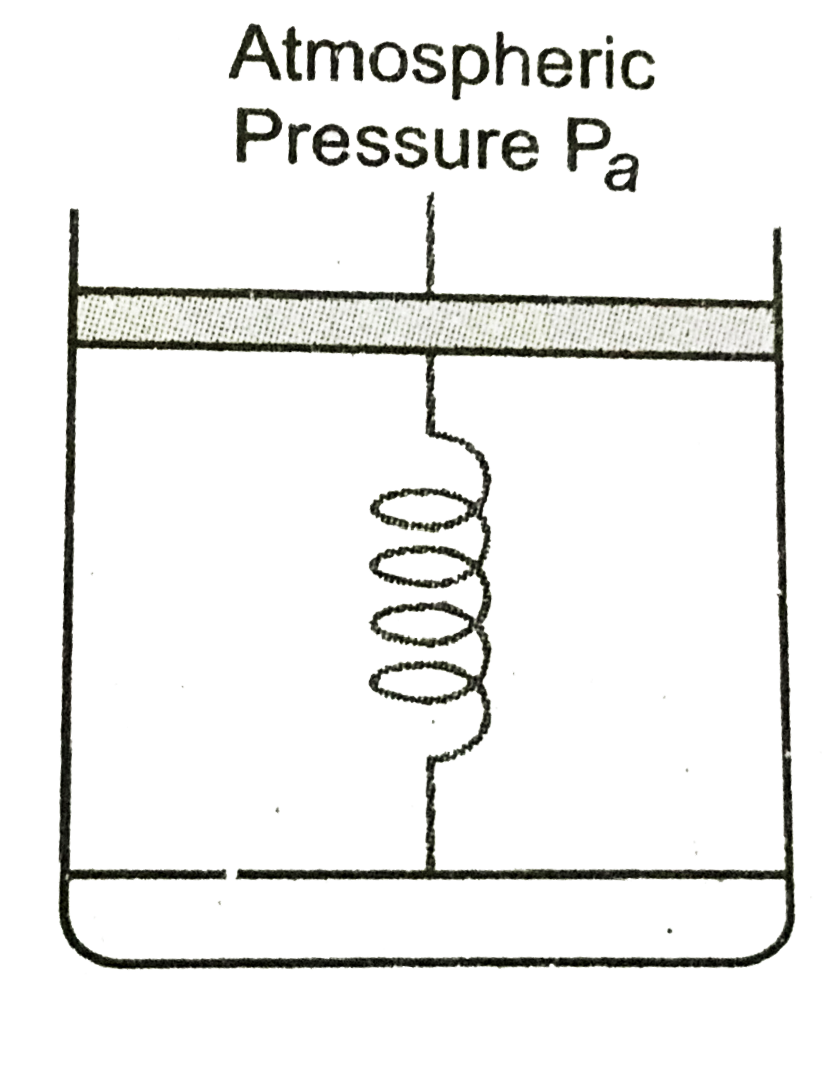
(a) Initially, the spring is unstretched and the gas is in equilibrium, therefore, initial pressure of the system = atmospheric pressure=
(b) On supplying heat, the gas expands from .
Increase in volume of gas
As cross sectional are of piston, ,
extension in spring ,
Force exerted by stretched spring on the piston,
Final pressure of the system,
(c ) If is final temp. of the gas, then increase in internal energy,
Where , and
Also,
From first law of thermodynamics,
This is the required. relation.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Higher order thinking skills
9 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Value based Questions
4 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Short answer questions(NCERT)
6 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assertion-Reason Type Questions
24 Videos
Similar Questions
Consider one mole of perfect gas on a cylinder of units cross-section with a piston attched (figure). A spring (spring constant K ) is attched (unstrecthed lengthL ) to the piston and to the bottom of the cylinder . Inditially the spring is unstrecthed and the gas is in equailibrium. A certain amount of heat Q is supplied to the gas causing an increase of value from V0 to V1.
(a) What is the initial pressure of the system ?
(b) What is the final pressure of the system?
(c) Using the first law of thermodynamic, write down a relation between Q,pa,V,V0 and K.

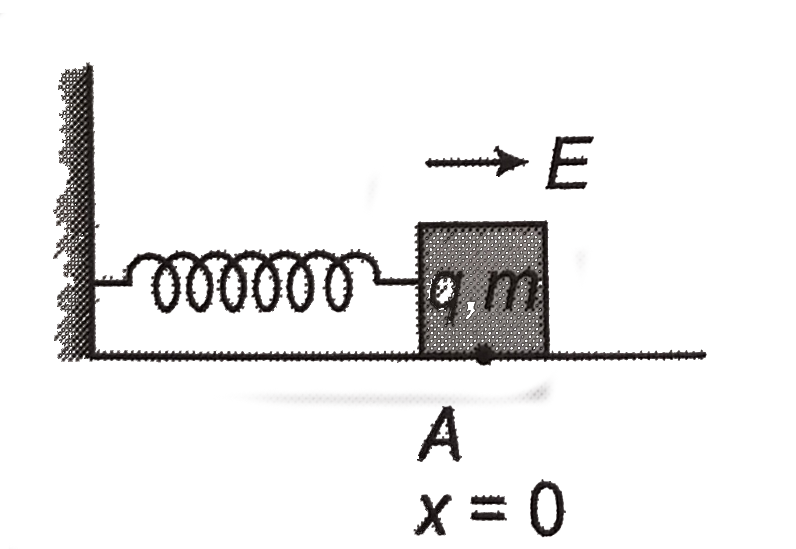
View SolutionA block of mass m having charge q is attached to a spring of spring constant k. This arrangement is placed in uniform electric field E on smooth horizontal surface as shown in the figure. Initially spring in unstretched. Find the extension of spring in equilibrium position and maximum extension of spring.
View Solution
Knowledge Check
In the equilibrium conditions shown in the figure all the springs have unstretched length l
 Aspring constant of all the spring is sameBspring constant of third spring is maximumCspring force is minimum in second springDspring constant is maximum in fourth spring
Aspring constant of all the spring is sameBspring constant of third spring is maximumCspring force is minimum in second springDspring constant is maximum in fourth springA metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
Ak=YA/LBk=2YA/LCk=YA/2LDk=YL/AAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
A(a) 4MgkB(b) 2MgkC(c) MgkD(d) Mg2k
One mole of a perfect gas in a cylinder fitted with a piston has a pressure P, volume V and temperature T. if the temperature is increased by 1K keeping pressure constant, the increase in volume is
View SolutionConsider the situation shown in figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the puley, find the maximum eleongation of the spring.
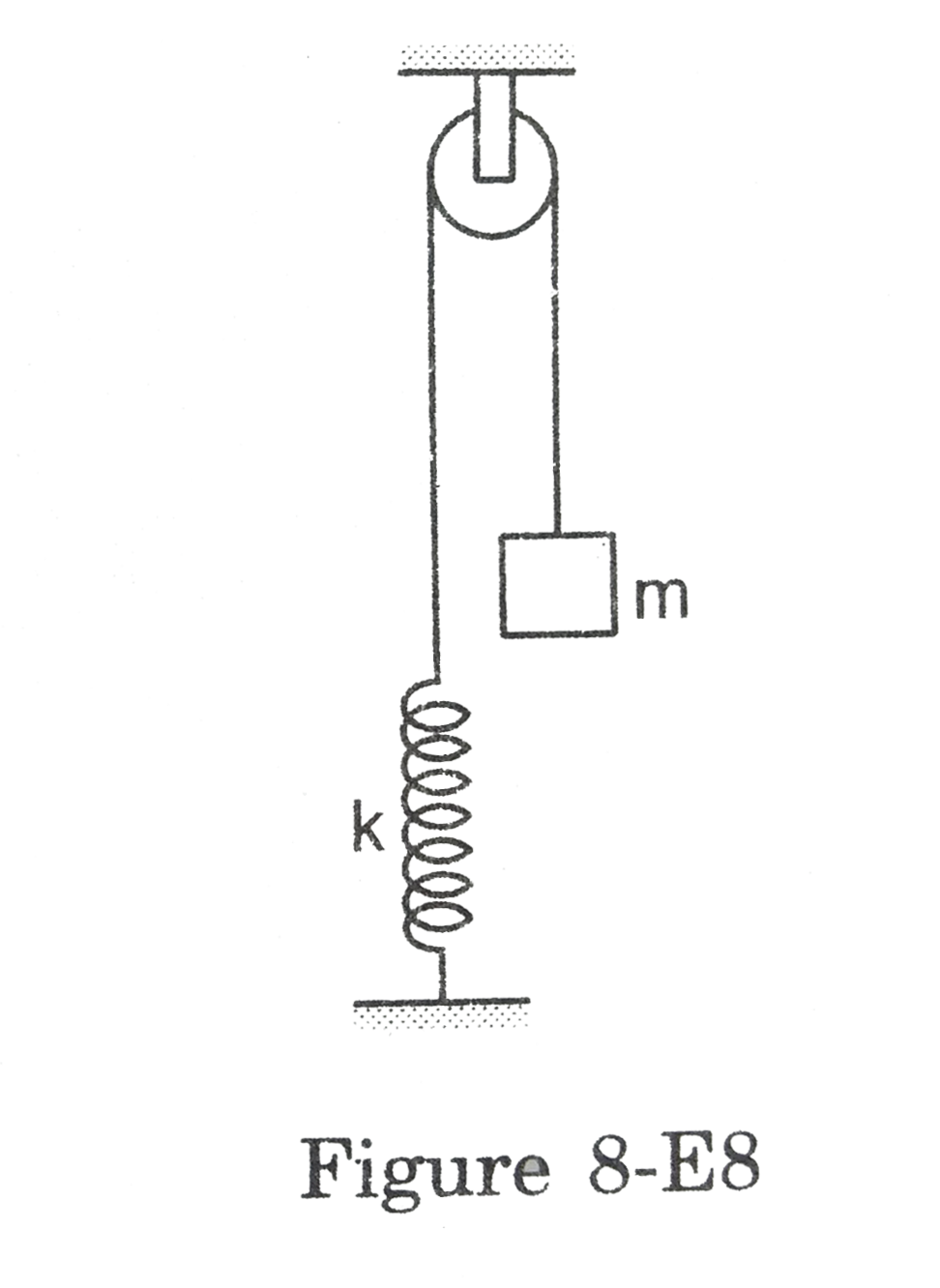
View SolutionA small ball of mass M=1 kg is attached to two identical springs of constant 100N/m, which are attached to floor and roof. The springs are initially unstretched. By what distance ball comes down to attain equilibrium? (in cm)

View SolutionA horizontal cylinder has two sections of unequal cross - sections, in which two pistons can move freely. The pistons are joined by a string, Some gas is trapped between the pistons. If this gas is heated the pistons will

View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)

View Solution
